bzoj2655calc 容斥+dp

2655: calc

Time Limit: 30 Sec  Memory Limit: 512 MB
Submit: 322  Solved: 197
[Submit][Status][Discuss]

Description

　　一个序列a1,...,an是合法的，当且仅当：
　　长度为给定的n。
　　a1,...,an都是[1,A]中的整数。
　　a1,...,an互不相等。
　　一个序列的值定义为它里面所有数的乘积，即a1a2...an。
　　求所有不同合法序列的值的和。
　　两个序列不同当且仅当他们任意一位不一样。
　　输出答案对一个数mod取余的结果。

Input

　　一行3个数，A，n，mod。意义为上面所说的。

Output

　　一行结果。

Sample Input

9 7 10007

Sample Output

3611

HINT

数据规模和约定
　　0:A<=10,n<=10。
　　1..3:A<=1000,n<=20.
　　4..9:A<=10^9,n<=20
　　10..19:A<=10^9,n<=500。
　　全部:mod<=10^9,并且mod为素数，mod>A>n+1

 

算法1

容斥法：
推荐blog
http://blog.csdn.net/qq_20669971/article/details/52790835

有一点不是很懂,就是那个统计f数组时阶乘那里

又想了一下,大概是每次填数,我们是从前向后填的,
而实际上,是可以任意顺序填的,虽然f[i-j]贡献的答案是一样的,
但i-j个格子不同,填数的方案不同,应该多算几次

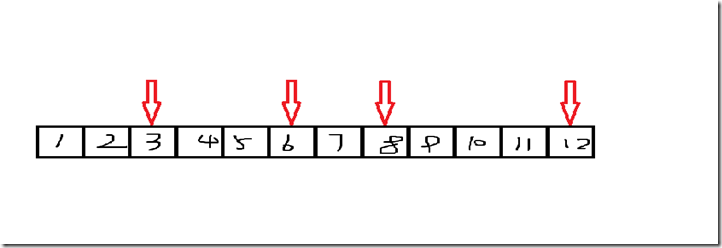
例如下面这张图片,现在该填12的位置,考虑重复4个位置,C(11,3)*f[8]选出了3 6 8三个位置贡献答案

实际上是可以先填上3 或6 或8再填两边,虽然都是f[8]贡献答案但是填数方案不同

先填3 那么得到的答案就是由[1,2][4,11]转移的

先填6 那么得到的答案就是由[1,5][7,11]转移的

先填8 那么得到的答案就是由[1,7][9,11]转移的

而每一层都需要这样考虑,所以 *3!

 

算法2

暴力法。

f[i][j]表示前i个格子,第i个格子填<=j的数的方案数
f[i][j]=f[i-1][j-1]*j+f[i][j-1]   复杂度O(nA)

第二维枚举A是肯定要TLE的,考虑优化
可以观察出这个东西可以表示成一个最高次为2n的多项式,未知数为j
那么就可以用拉格朗日求啦

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define ll long long
#define N 605
using namespace std;
ll inv[N],c[N][N],fac[N],g[N],f[N],A,n,mod;
int main(){
    cin>>A>>n>>mod;
    fac[0]=1;inv[1]=1;
    for(int i=1;i<=510;i++)
    fac[i]=(fac[i-1]*i)%mod;
    for(int i=2;i<=510;i++)
    inv[i]=(1ll*(mod-mod/i)*inv[mod%i])%mod;
    for(int i=0;i<=n;i++)c[i][i]=c[i][0]=1;
    for(int i=1;i<=510;i++)
    for(int j=1;j<i;j++)
    c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
    g[0]=(A+1)%mod;g[1]=(1ll*A*(A+1)>>1)%mod;
    ll t=(A+1)*(A+1)%mod;
    for(int i=2;i<=n;i++){
        t=((A+1)*t)%mod;
        ll sum=(A+1)%mod;
        for(int j=1;j<i;j++)
        sum=(sum+1ll*c[i+1][j]*g[j]%mod)%mod;
        sum=(t-sum)%mod;
        sum<0?sum+=mod:1;
        g[i]=(sum*inv[i+1])%mod;
    }
    f[0]=1;f[1]=(1ll*(A+1)*A>>1)%mod;
    for(int i=2;i<=n;i++){
        f[i]=g[1]*f[i-1]%mod;
        ll fg=-1;
        for(int j=i-2;~j;j--){
            f[i]=(f[i]+1ll*fg*fac[i-1-j]%mod*c[i-1][i-1-j]%mod*g[i-j]%mod*f[j]%mod+mod)%mod;
            fg=-fg;
        }
    }
    cout<<f[n];
    return 0;
}