四则运算

1.需求分析

　　　　　　　　　　　　　　　　

1）有乘除法，容易实现，需求明了。

2）有括号，根据需求有括号必定是2项以上的运算。要求一个算术式里面有2个级两个以上的算术符，但是没有具体要求有多少所以我们控制运算符在3个以内

3）数值范围，因为用户是4年级的小朋友，所以范围不能太大

4）加减无负数，因该说的事生成的计算数里面不能有负数，而且结果无负数。

5）除法无余数，除法结果不能有余数

6）支持分数，不能有余数，可以支持分数为计算数，结果也可以为计算数

7）支持小数，这个需求是最迷茫的。根据需求5说除法无余数，需求6又说支持分数，怎么会出现小数，难道是有些计算数里面有小数，好吧

8）打印中间每行的间隔。客户可能考虑的是我们可能会用控制台输出，所以直接说每行的间隔

2.算法设计

　　1.）数据结构

　　因为上一个二则运算较简单所以采用数据结构是数组，然后顺利成章的一开始想到的使用数组来保存表达式，结果在一对表达式的操作非常的复杂。然后就换成了树来保存表达式的结构。

　　需要支持分式，就意味着每个节点你保存的数据个数和类型是不同的。所以节点的数据类型可以加一个标志位区别。

class Atomic{
public:
    int type;//标志位
    int molecule, denominator;
};

　　2）如何控制运算符生成

　　在这个算法上我想尽量生成一个左右权重相差较小的二叉树（非常傻的想法，因为这样没有什么用），所以我采用一个将要生成运算符的个数分成2份传给左右子树

if(dataType && dataType % 2){ //将剩下生成的个数均匀的分给左右dataType是个数
      creatTree(root->leftChildren, dataType/2 + 1);
      creatTree(root->rightChildren, dataType/2);
}else{
      creatTree(root->leftChildren, dataType/2);
      creatTree(root->rightChildren, dataType/2);
}

　　3）实现减法无负数

　　这个在我采用二叉树数据结构的时候就显得非常的简单了，因为我们只需要将左右子树交换下位置就好了

if((leftSum - rightSum) < 0){
    TreeNode *temp = root->leftChildren;
    root->leftChildren = root->rightChildren;
    root->rightChildren = temp;
    return rightSum - leftSum;
}else{
   return leftSum - rightSum;
}

 　　4）支持分数

　　这个功能只实现一半，因为我发现我想了控制无余数的办法，最后我失败了，所以这是个半成品。但是有个想法就是控制结果生成等式，但是实在没想好。好吧，这个需求没满足客户。

3.结果展示

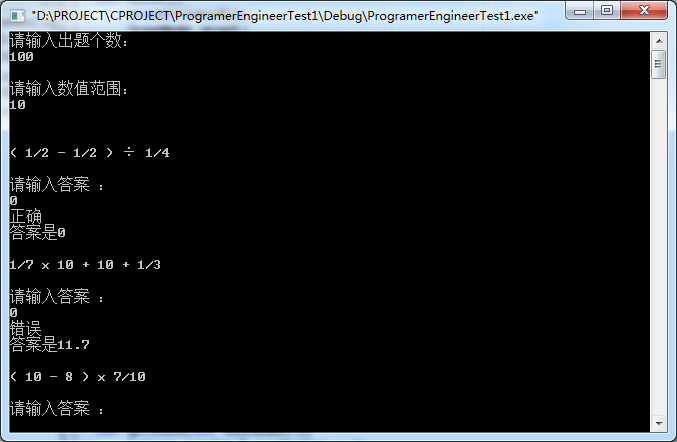
总结

1）界面没有做好，给用户的体验太差了。