图论——线段树优化建图

链接：CF786B Legacy

题意：

有一个n个节点的有向有权图
有三种类型的边：
1.从u到v的一条边权为w的边
2.从u到区间[l,r]任意一个点都有一条边权为w的边
3.从区间[l,r]中任意一个点到v点都有一条边权为w的边
求从点1到其他所有点的最短路。若不可达，则输出-1

题解：

第一种类型的边很容易建立，但对于第二、三种类型的边，如果采用区间每一个点都连边的方式，连边数量太多不可接受。
考虑到是区间问题，我们可以采用线段树优化建图的方式解决。
建立两颗线段树，第一颗存储的是入边的线段树，也就是单点到区间这样的边，另外一颗就是出边的线段树。
用第二种类型的边举例：
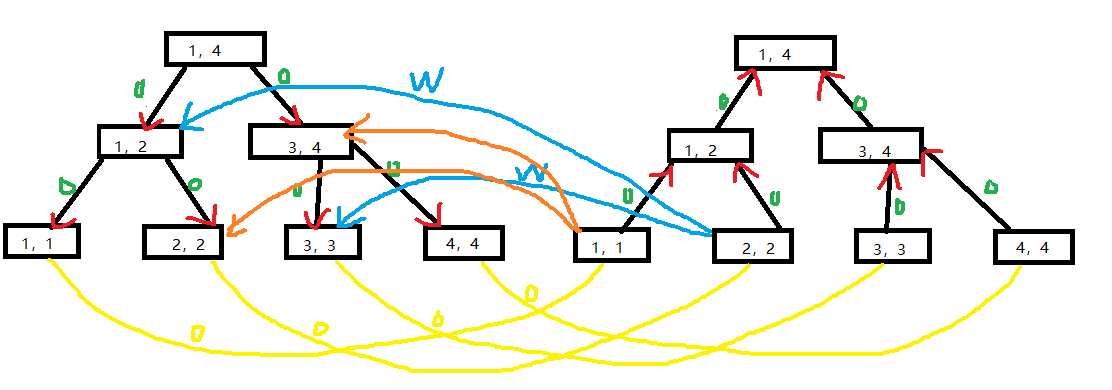
假设有这样的一条边：2——>[1,3],边权为w，n = 4
则我们需要将出边树的叶子节点[2,2]向入边树的节点[1,2]与[3,3]连边，边权为w
而线段树内部点之间的边权定为0，则建图大概就是这样的：

第三种类型的边就是出边树若干个节点向入边树的一个叶子节点连边即可
还需要考虑一点的是：因为左右两边叶子节点都是代表原图中的某个节点，因此我们需要将叶子节点一一对应的连接起来，边权为0

/*
线段树优化建图
*/
#include <bits/stdc++.h>
using namespace std;

#define mp make_pair
#define pb push_back
typedef long long ll;
typedef pair<ll,int> pii;
const int maxn = 1e5+10;
const ll inf = (1ll<<55);
vector<pii> G[maxn*20];
int n,q,s;
int base;
int tree[maxn*20];
void add(int u,int v,int w){
    G[u].pb(mp(w,v));
}

void build(int l,int r,int p){
    if(l == r){
        tree[l] = p;
        return ;
    }
    add(p,p<<1,0),add(p,p<<1|1,0);
    add(base+(p<<1),base+p,0),add(base+(p<<1|1),base+p,0);
    int m = (l+r)>>1;
    build(l,m,p<<1);
    build(m+1,r,p<<1|1);
}

void update(int op,int v,int w,int L,int R,int l,int r,int p){
    // if(L>r || R<L) return ;
    if(L<=l && r<=R){
        if(op == 2) add(v+base,p,w);
        else if(op == 3) add(p+base,v,w);
        return ;
    }
    int m = (l+r)>>1;
    if(L<=m) update(op,v,w,L,R,l,m,p<<1);
    if(R>m) update(op,v,w,L,R,m+1,r,p<<1|1);
}

ll dis[maxn*20];
bool vis[maxn*20];

void dij(int s){
    memset(dis,0x3f,sizeof(dis));
    dis[s] = 0;

    priority_queue<pii,vector<pii>,greater<pii> > q;
    q.push(mp(0,s));

    while(!q.empty()){
        int u=q.top().second;
        q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for (auto i : G[u]){
            int v=i.second;
            ll w=i.first;
            if(dis[v] > dis[u] + w){
                dis[v]=dis[u]+w;
                q.push(mp(dis[v],v));
            }
        }
    }
}

int main(){
    cin>>n>>q>>s;
    base = 1000000;
    build(1,n,1);
    for (int i=1;i<=n;i++){
        add(tree[i],tree[i]+base,0);
        add(tree[i]+base,tree[i],0);
    }
    
    for (int i=1;i<=q;i++){
        int op;
        scanf("%d",&op);
        
        if(op == 1){
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            if(u == v) continue;
            add(tree[u],tree[v],w);
        }
        else {
            int v,l,r,w;
            scanf("%d%d%d%d",&v,&l,&r,&w);
            update(op,tree[v],w,l,r,1,n,1);
        }
    }

    dij(tree[s]);
    for (int i=1;i<=n;i++){
        printf("%lld ",dis[tree[i]] >= inf ? -1 : dis[tree[i]]);
    }
    return 0;
}