题目链接:点击打开链接
Imp is in a magic forest, where xorangles grow (wut?)

A xorangle of order n is such a non-degenerate triangle, that lengths of its sides are integers not exceeding n, and the xor-sum of the lengths is equal to zero. Imp has to count the number of distinct xorangles of order n to get out of the forest.
Formally, for a given integer n you have to find the number of such triples (a, b, c), that:
- 1 ≤ a ≤ b ≤ c ≤ n;
 , where
, where 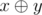 denotes the bitwise xor of integers x and y.
denotes the bitwise xor of integers x and y.- (a, b, c) form a non-degenerate (with strictly positive area) triangle.
The only line contains a single integer n (1 ≤ n ≤ 2500).
Print the number of xorangles of order n.
6
1
10
2
The only xorangle in the first sample is (3, 5, 6).
题意:没错这就是一个枚举三角形三条边的题目,不过由于要求a ^ b ^ c = 0,所以这一题只需要o(n²)就能枚举完
下面来看这条件啥意思:我们先看两个值异或啥意思,a^ b = 0 :异或异或,a和b的二进制每一位异的话就是1,不异的话就是0,a^b也就是说a和b的每一位都相同,也就是a == b!
那么a^b^c=0啥意思?将a^b看成一个整体呗,也就是三角形的第三条边的值为a^b,只要保证a^b满足第三条边就阔以了。
其他还有啥坑点?我们来学下英语。。
xor 异或
non-degenerate triangle 非退化三角形, 也就是正常的三角形,没有180度甚至以上的角的三角形。
⊕ 这符号也是异或。。
我们顺便来看下异或的其他性质吧
其实现场想一下推到还是能推出来的
这题就不贴代码了。。