1. 什么是吉布斯现象
1.1. 什么吉布斯现象?
矛盾性:在时域描述一个不连续的信号要求信号的有无穷的频率成分,但实际情况中不可能采样到无穷的频率成分。
实际中的信号采样系统只能采样一定的频率范围,对不连续信号(或有无穷频率成分的信号)采样将会存在频率截断。
频率截断会引起时域信号在不连续处产生“振铃效应”,这个现象成为吉布斯现象。
吉布斯现象:由于频率截断现象,具有无穷频率分量的信号在时域的不连续处会产生“振铃效应”。
- 对连续时间周期信号可以进行傅里叶级数展开,如果只取其中的前有限项,将得到信号的一个最小均方误差逼近。当项目增至无穷时,这个逼近在均方意义上收敛于原信号,但并不是一致收敛的。对于信号的跳变点,傅里叶级数的部分和将在该点附近出现波动,如将其输入理想低通滤波器,则相当于对其频率作了截断,将会出现类似的效果。
- Gibbs 现象的产生有两个条件:(1) 对信号频谱的锐截止;(2) 原信号存在跳变点
1.2. 吉布斯现象形成的原因?
吉布斯现象形成的原因是:频率截断。
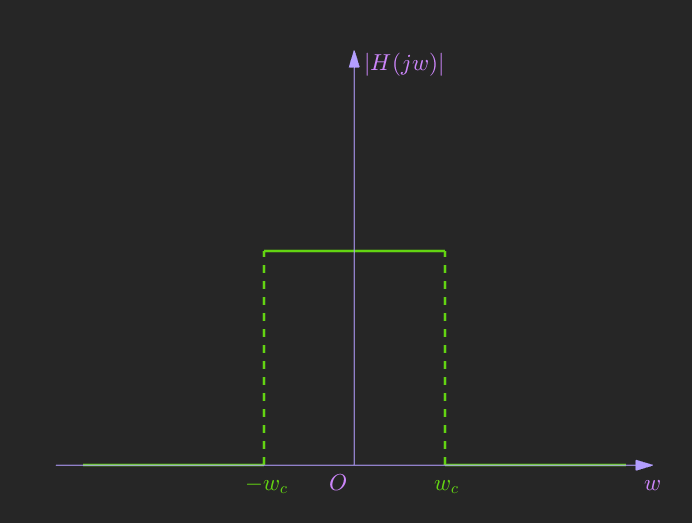
“频率截断”可以简单地理解为一个理想的低通滤波器(截止频率为(w_c)),如下图所示:
| 幅频特性 | 相频特性 |
|---|---|
 |
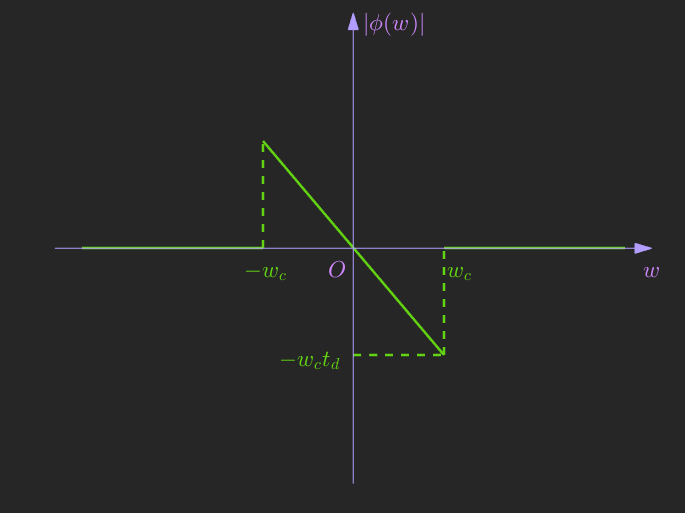 |
低通滤波器只保留(|w|le w_c)的频率成分,因此输入信号的高频部分将被截断,丢失了部分频率信息势必会在时域上产生一定的影响。
下面将分别考虑低通滤波器对单位阶跃信号,矩形脉冲信号,周期矩形脉冲信号的响应来分析吉布斯现象:
低通滤波器的单位阶跃响应
理想的低通滤波器的频率响应为
[H(jw) = G_{2w_c}(w)e^{-jwt_d}
]
则单位阶跃响应为
[egin{aligned}
S(jw) &= H(jw)mathscr{F}(u(t))\
&= G_{2w_c}(w)e^{-jwt_d}cdot [pi delta(w) + frac{1}{jw}]\
end{aligned}]
为求输出信号的时域波形,进行傅里叶反变换,有
[egin{aligned}
s(t) &= mathscr{F}^{-1}(S(jw))\
&= frac{1}{2pi}int_{-w_c}^{w_c} [pi delta(w) + frac{1}{jw}]e^{-jwt_d}cdot e^{jwt} mathrm{dw}\
&= frac{1}{2} + int_{-w_c}^{w_c}frac{1}{jw} e^{jw(t-t_d)} mathrm{dw}\
&= frac{1}{2} + frac{1}{2pi}int_{-w_c}^{w_c}frac{1}{jw}cos{[w(t-t_d)]}mathrm{dw} + frac{1}{2pi}int_{-w_c}^{w_c}frac{1}{w}sin{[w(t-t_d)]}mathrm{dw}\
&= frac{1}{2} + frac{1}{pi}int_{0}^{w_c}frac{1}{w}sin{[w(t-t_d)]}mathrm{dw}\
&= frac{1}{2} + frac{1}{pi}int_{0}^{w_c(t-t_d)} frac{sin x}{x} dx
end{aligned}]
其中上式的积分部分称为正弦积分。输出信号的时域波形如图所示,它具有以下特点:

理想低通滤波器的单位阶跃响应
- 输出波形存在吉布斯波纹,它的振荡频率等于(frac{2pi}{w_c});
- 上升沿之前存在一个幅度最大的负向振峰(预冲),在上升之后存在一个幅度最大的正向振峰(过冲)。无论截止频率(w_c)多大,只要(w_c < infty),过冲和预冲的幅度总是稳定值的9%;
- 上升沿从预冲到过冲的时间与截止频率有关,即(t_r = frac{2pi}{w_c}),即(w_c)越大,上升越快,吉布斯波纹振荡越明显(趋于无穷时,相当于阶跃)
低通滤波器对矩形脉冲信号的响应
矩形脉冲信号可以看成两个阶跃信号的相减,故输出信号可以看成低通滤波器的两个阶跃响应之差,易想象同样存在吉布斯现象。
[G_{ au}(t)=u(t) - u(t- au)
]
低通滤波器对周期矩形脉冲信号的响应
设周期方波信号的周期为(T=2 au),则周期方波信号可以表示为
[f(t) = 2G_{ au}(t) * delta_{2 au}(t) - 1
]
其频谱为((Omega = frac{2pi}{2 au}=frac{pi}{ au}))
[egin{aligned}
F(jw) &= 2 au Sa(frac{ au}{2}w) Omega delta_{_{Omega}}(w) - 2pidelta(w)\
&= sum_{n=-infty atop n
ot =0}^{n=+infty} 2pi Sa(frac{npi}{2}) delta(w - nOmega)
end{aligned}]
显然,则是一个偶函数((F(jw))为纯实数),也是一个奇谐函数(只有奇次谐波分量)。再考虑理想低通滤波器,其输出相应相当于只取(|w| < w_c)的频率分量,可以发现:
- 当(w_c gg Omega) 时,输出信号较为接近原输入信号,但是在不连续处存在预冲和过冲现象;
- 随着(w_c)逐渐减小,上升沿变得缓慢(陡度降低),吉布斯波纹周期变长;
- 当(w_c)接近(Omega)时,输出信号退化为频率等于基频(Omega)的正弦波。
1.3. 如何减小吉布斯现象?
- 低通滤波器对信号频谱进行频域加窗,频窗有限引起时域的吉布斯波纹,可以考虑其它的频窗,如三角窗等
- 另外,对时域加窗(时域截断)也会出现的吉布斯波纹,因此需要选择好合适的窗函数。