偏函数
偏函数介绍
Scala的函数是基于Function家族,0-22,一共23个Function Trait可以被使用,数字代表了Funtcion的入参个数。
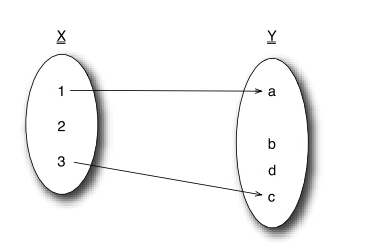
偏函数:f : X -> Y,该函数仅定义了输入参数X的子集1和3,没有包含2。
在Scala中的偏函数是通过特质PartialFunction[-A, +B]来定义的,查看PatialFunction特质的API,可看到PatialFunction定义如下:
trait PartialFunction[-A, +B] extends (A) ⇒ B
可以看出偏函数:
1)是一个将类型A转为类型B的特质。。接受A类型的输入参数,返回值为B类型。第一个表示参数类型,第二个表示返回参数。所以偏函数只有一个入参,PartialFunction其实是Funtion1的子类
2)是一个一元函数,“-”符号作用于类型表示逆变,-A表明输入参数为A类型或A类型的父类,也就是说输入的参数应为A的子集,具有“部分”的含义。
3)函数有可能“偏”离了A定义域(Type)类型,而成为值域B, +表明可以是B或B的子类,具有“全部”的含义。
例题:一个集合val list = List(1, 2, 3, 4, "abc")
忽略集合list非数字的元素,将的所有数字+1,并返回一个新的集合。结果是:(2, 3, 4, 5)
val list = List(1, 2, 3, 4, "hello")
//定义一个偏函数
//1. PartialFunction[Any,Int] 表示偏函数接收的参数类型是Any,返回类型是Int
//2. isDefinedAt(x: Any) 如果返回true ,就会去调用 apply 构建对象实例,如果是false,过滤
//3. apply 构造器 ,对传入的值 + 1,并返回(新的集合)
val partialFun = new PartialFunction[Any,Int] {
override def isDefinedAt(x: Any): Boolean = {
println("x=" + x)
x.isInstanceOf[Int]
}
override def apply(v1: Any): Int = {
println("v1=" + v1)
v1.asInstanceOf[Int] + 1
}
}
//使用偏函数
//说明:如果是使用偏函数,则不能使用map,应该使用collect
//说明一下偏函数的执行流程
//1. 遍历list所有元素
//2. 然后调用 val element = if(partialFun-isDefinedAt(list单个元素)) {partialFun-apply(list单个元素) }
//3. 每得到一个 element,放入到新的集合,最后返回
val list2 = list.collect(partialFun)
println("list2" + list2)
偏函数注释:
- 当使用偏函数时,会遍历集合的所有元素,编译器执行流程时先执行isDefinedAt()如果为true ,就会执行 apply, 构建一个新的Int 对象返回
- 执行isDefinedAt() 为false 就过滤掉这个元素,即不构建新的Int对象.
- collect函数支持偏函数,而map函数不支持偏函数,因为map底层的机制就是所有循环遍历,无法过滤处理原来集合的元素
不使用偏函数的问题:
//思路1 filter + map 方式解决
//虽然可以解决问题,但是麻烦.
val list = List(1, 2, 3, 4, "hello")
// 先过滤,再map
println(list.filter(f1).map(f3).map(f2))
//思路2-模式匹配
//小结:虽然使用模式匹配比较简单,但是不够完美
val list2 = list.map(addOne2)
println("list2=" + list2)
}
//模式匹配
def addOne2( i : Any ): Any = {
i match {
case x:Int => x + 1
case _ =>
}
}
def f1(n: Any): Boolean = { n.isInstanceOf[Int]}
def f2(n: Int): Int = { n + 1}
//将Any->Int [map]
def f3(n: Any): Int = {n.asInstanceOf[Int] }
偏函数的简化方法
简化方法一:定义偏函数中使用case

简化方法二:直接在collect中使用case

作为参数的函数
函数作为一个变量传入到了另一个函数中
val list = List(1, 2, 3, 4)
def plus3(x:Int): Int =x+3
println(list.map(plus3))
println(list.map(plus3(_)))
- map(plus(_)) 中的plus(_) 就是将plus这个函数当做一个参数传给了map,_这里代表从集合中遍历出来的一个元素。
- plus(_) 这里也可以写成 plus 表示对 Array(1,2,3,4) 遍历,将每次遍历的元素传给plus的 x
- 进行 3 + x 运算后,返回新的Int ,并加入到新的集合中
- def map[B, That](f: A => B) 的声明中的 f: A => B 一个函数
匿名函数
基本介绍
没有名字的函数就是匿名函数,可以通过函数表达式=>来设置匿名函数
应用实例
val triple = (x: Double) => 3 * x println(triple(3))

说明
- (x: Double) => 3 * x 就是匿名函数
- (x: Double) 是形参列表, => 是规定语法表示后面是函数体, 3 * x 就是函数体,如果有多行,可以 {} 换行写.
- triple 是指向匿名函数的变量。
高阶函数
基本介绍
能够接受函数作为参数的函数,叫做高阶函数 (higher-order function)。可使应用程序更加健壮。
高阶函数可以入参是函数类型
scala> def ff(f: Double => Double, n1: Double) = {f(n1)}
ff: (f: Double => Double, n1: Double)Double
scala> //sum 是接收一个Double,返回一个Double
scala> def sum(d: Double): Double = {d + d}
sum: (d: Double)Double
scala> val res = ff(sum, 6.0)
res: Double = 12.0
scala> println("res=" + res)
res=12.0
高阶函数可以返回函数类型
scala> def subxy(x: Int) = {
| (y: Int) => x - y //匿名函数
| }
subxy: (x: Int)Int => Int
scala> val res = subxy(3)(5)
res: Int = -2
scala> println(res)
-2
参数(类型)推断
基本介绍
参数推断省去类型信息(在某些情况下[需要有应用场景],参数类型是可以推断出来),同时也可以进行相应的简写。
参数类型推断写法说明
- 参数类型是可以推断时,可以省略参数类型当传入的函数,只有单个参数时,可以省去括号。
- 如果变量只在=>右边只出现一次,可以用_来代替
val list = List(1, 2, 3, 4)
println(list.map((x:Int)=>x + 1)) //(2,3,4,5)
println(list.map((x)=>x + 1)) //(2,3,4,5)
println(list.map(x=>x + 1)) //(2,3,4,5)
println(list.map( _ + 1)) //(2,3,4,5)
println(list.reduce((n1:Int ,n2:Int) => n1 + n2)) //10
println(list.reduce((n1 ,n2) => n1 + n2)) //10
println(list.reduce( _ + _)) //10
- map是一个高阶函数,因此也可以直接传入一个匿名函数,完成map
- 当遍历list时,参数类型是可以推断出来的,可以省略数据类型Int>>println(list.map((x)=>x + 1))
- 当传入的函数,只有单个参数时,可以省去括号println(list.map(x=>x + 1))
- 如果变量只在=>右边只出现一次,可以用_来代替println(list.map(_ + 1))
函数的闭包
基本介绍
基本介绍:闭包就是一个函数和与其相关的引用环境组合的一个整体(实体)。
是不是感觉很抽象?那你需要读一下下面的内容:
假设你现在有一个函数 f (x) = a + x 这个函数是不完整的,比如 f (1) = a + 1 你还差一个问题: a 是多少?
有两个方法回答这个问题:
第一种叫“动态作用域”,a的值决定于函数调用时上下文中a的值,比如a = 1;v=f(1) ; 这里v为2动态作用域的问题是,函数每一次调用相同的参数未必返回相同的值,其返回值还取决于上下文的某些值
第二种是“词法作用域”,a的值取决于函数定义时上下文中的值g (a) = lambda (x) a + x;f = g(2)这里函数g返回一个和上面函数f形式一样函数,a在此处为2,那么执行a = 1;v=f(1) ;这里v为3因为f要“记住”自己定义时a的值为2,所以实现时 f (x) = a + x 和 a = 2 被打包在一块,被称为“闭包”,意思是它是完整独立的,仅仅依靠调用时参数求值,不再依赖调用时的上下文。
这是知乎大佬讲的,其实说的很明白了。
我们来看一下百科的解释:
在计算机科学中,闭包(Closure)是词法闭包(Lexical Closure)的简称,是引用了自由变量的函数。这个被引用的自由变量将和这个函数一同存在,即使已经离开了创造它的环境也不例外。
所以,有另一种说法认为闭包是由函数和与其相关的引用环境组合而成的实体。 Peter J. Landin 在1964年将术语闭包定义为一种包含环境成分和控制成分的实体。
闭包是可以包含自由(未绑定到特定对象)变量的代码块;这些变量不是在这个代码块内或者任何全局上下文中定义的,而是在定义代码块的环境中定义(局部变量)。“闭包” 一词来源于以下两者的结合:要执行的代码块(由于自由变量被包含在代码块中,这些自由变量以及它们引用的对象没有被释放)和为自由变量提供绑定的计算环境(作用域)。在 Scala、Scheme、Common Lisp、Smalltalk、Groovy、JavaScript、Ruby、 Python、Go、Lua、objective c、swift 以及Java(Java8及以上)等语言中都能找到对闭包不同程度的支持。
在离散数学(具体的说是抽象代数)里,如果对一个集合中的每个元素执行某个运算操作,得到的结果还是这个集合的元素,那么就说该集合在这个运算操作下构成闭包。例如,整数集合在减法运算下构成闭包;但是自然数在减法运算下不构成闭包。
封闭的定义
有了集合和运算的概念,就可以定义封闭的概念了。
非正式地,如果定义于集合A上的运算+的运算结果仍然属于A,那么运算+对于集合A是封闭的。下面给出“封闭”的一个半形式化定义:
如果对于任意a1,a2∈A,有a1+a2∈A,那么说二元运算+对于集合A是封闭的。(⊙,+ 与”,“或”)
例如“+”对于N+是封闭的,因为任意两个正整数的和结果仍然是正整数;但是“>”对于N+不是封闭的,例如3和5属于N+,但是:3>5=>2∉N+。
闭包性质
一个集合满足闭包性质当且仅当这个集合在某个运算或某些运算的搜集下是封闭的,其中“某些运算的搜集下封闭”是指这个集合单独闭合在每个运算之下。
值得一提的是,之前这条定义往往被作为一条公理引入一个代数结构,叫做“闭包公理”。但是现代集合论往往将运算形式化的定义为集合间的运算,所以将其作为公理引入代数结构是多余的(因为可以通过其它公理间接定义闭包公理),但是对于子集是否闭合的问题,闭包公理仍然有意义。
scala中的闭包
scala> def subxy(x: Int) = {
| (y: Int) => x - y //匿名函数
| }
subxy: (x: Int)Int => Int
scala> val res = subxy(3)(5)
res: Int = -2
scala> println(res)
-2
- (y: Int) => x – y返回的是一个匿名函数 ,因为该函数引用函数外的 x,那么 该函数和x整体形成一个闭包 如:这里 val f = subxy(20) 的f函数就是闭包
- 返回函数是一个对象,而x就是该对象的一个字段,他们共同形成一个闭包,当多次调用f时(可以理解多次调用闭包),发现使用的是同一个x, 所以x不变。
- 在使用闭包时,主要搞清楚返回函数引用了函数外的哪些变量,因为他们会组合成一个整体(实体),形成一个闭包
函数柯里化(curry)
函数编程中,接受多个参数的函数都可以转化为接受单个参数的函数,这个转化过程就叫柯里化
柯里化就是证明了函数只需要一个参数而已。
scala> def mulCurry2(x: Int)(y:Int) = x * y mulCurry2: (x: Int)(y: Int)Int scala> println(mulCurry2(10)(8)) 80
案例:
比较两个字符串在忽略大小写的情况下是否相等,注意这个是两个任务:
- 全部转大写(或小写)
- 比较是否相等
//eq函数,可以接收两个字符串,比较是否相等
def eq(s1: String, s2: String): Boolean = {
s1.equals(s2)
}
//隐式类
implicit class implicit_toString(s: String) {
//体现了将比较字符串的事情,分解成两个任务完成
//1. checkEq 完转换大小写
//2. f函数完成比较任务
def checkEq(ss: String)(f: (String, String) => Boolean): Boolean = {
f(s.toLowerCase, ss.toLowerCase)
}
}
val str1 = "hello"
println(str1.checkEq("HeLLO")(eq))
简化本
println(str1.checkEq("HeLLO")(_.equals(_)))
控制抽象
控制抽象被描述为是一系列语句的聚集,是一种特殊的函数,因为它是本质上只是对一系列语句的封装,所以它理应:
1. 没有参数输入;
2. 没有值返回。
只有一个空值过程的:
scala> def repeat5(action: =>Unit)=for(i<-1 to 5)action repeat5: (action: => Unit)Unit scala> repeat5(println(1)) 1 1 1 1 1
其他参数+控制过程的:
scala> def repeat5(action: =>Unit)=for(i<-1 to 5)action repeat5: (action: => Unit)Unit scala> repeat5(println(1)) 1 1 1 1 1
克里化的
scala> def repeat(n:Int)(action: =>Unit)=for(i<-1 to n)action repeat: (n: Int)(action: => Unit)Unit scala> repeat(5)(println(1)) 1 1 1 1 1
scala中的抽象控制和高阶克里化函数有什么区别?

def void(): Unit ={println("---void")}
def sum1(x:Int): Int =x+1
def test1(f: Int => Int, f2:() =>Unit , n1: Int): Unit = {
f2()
println("====>"+f(n1))
f2()
}
test1(sum1,void,10)
def test2(f: Int => Int, f2: =>Unit , n1: Int): Unit = {
f2
println("====>"+f(n1))
f2
}
test2(sum1,void(),10)
其实抽象控制就是高阶函数一种特例哈哈