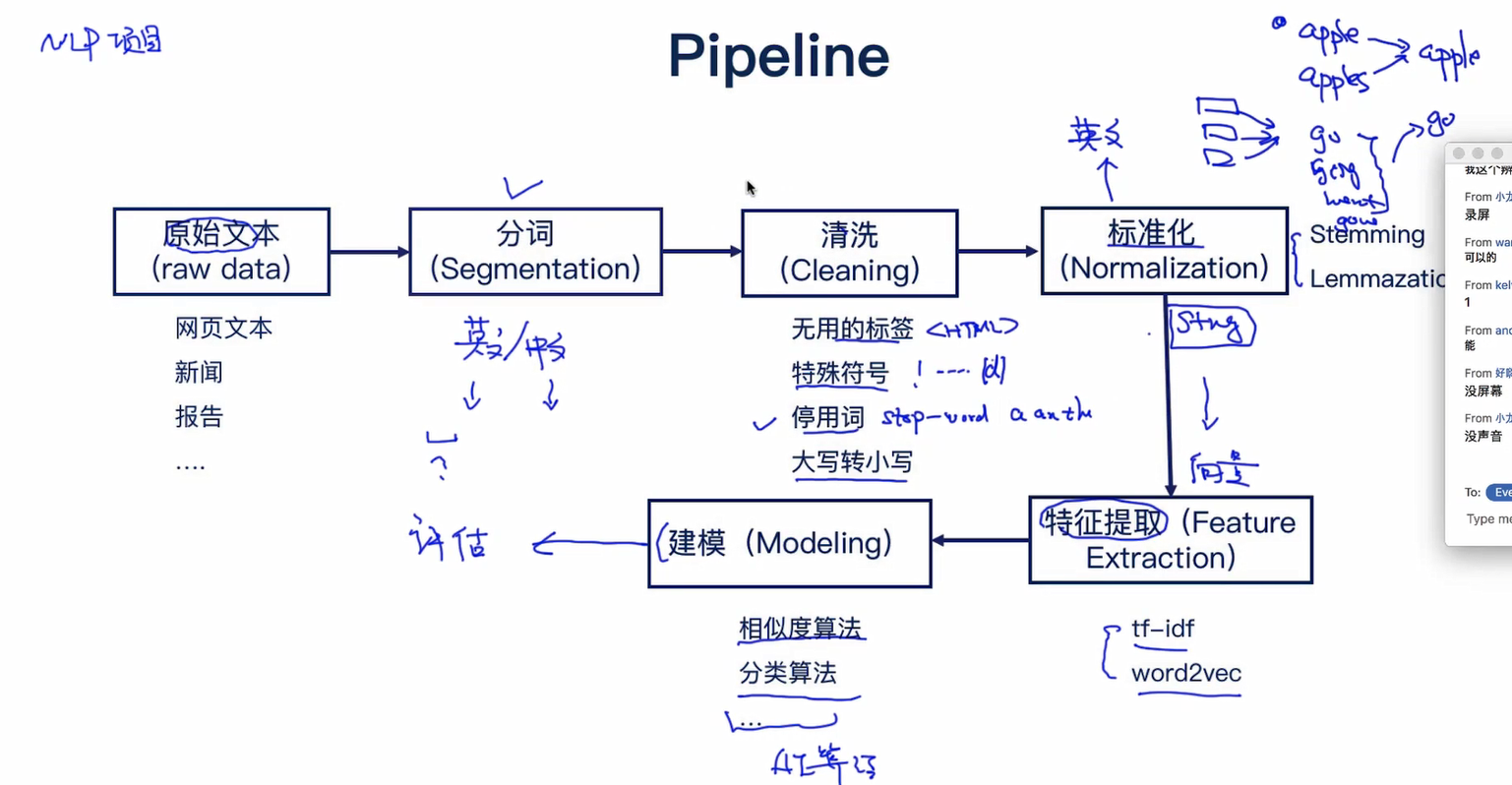
文本处理的流程

# encoding=utf-8 import jieba import warnings # 基于jieba的分词 seg_list = jieba.cut("贪心学院专注于人工智能教育", cut_all=False) print("Default Mode: " + "/ ".join(seg_list)) jieba.add_word("贪心学院") seg_list = jieba.cut("贪心学院专注于人工智能教育", cut_all=False) print("Default Mode: " + "/ ".join(seg_list))



缺点:
1.贪心算法可能只是局部最优
2.时间复杂度高
3.效率(max_len)
4.语义分歧


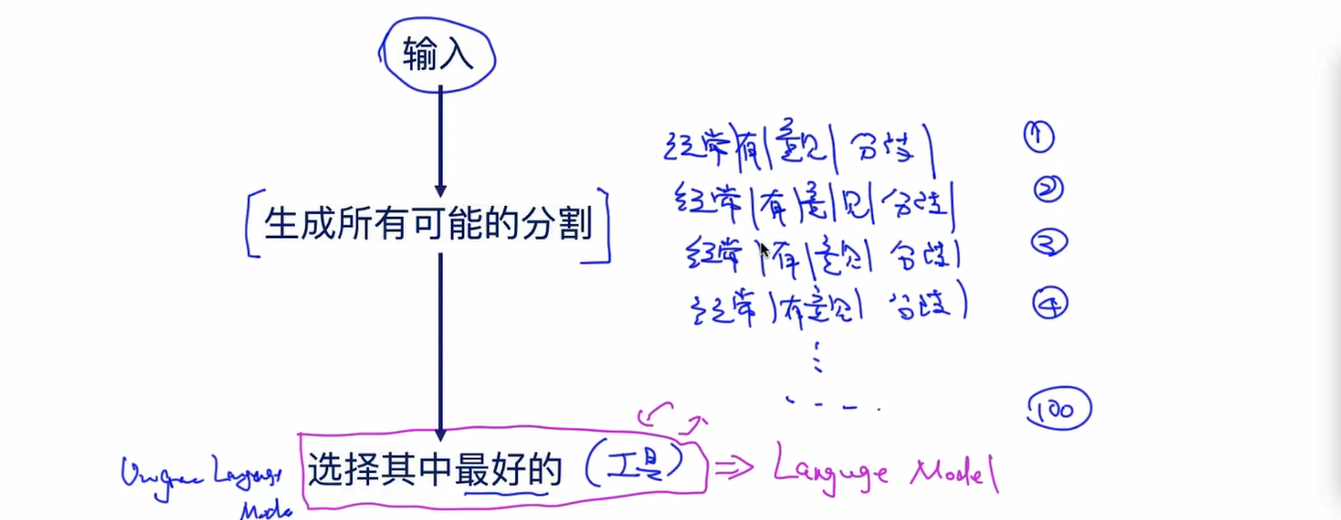


还有对第一次出现单词的处理以及平滑处理。以后再讲。
维特比算法登场:

维特比算法定义:
维特比算法是一种动态规划算法,用于寻找最有可能产生观测事件序列的-维特比路径-隐含状态序列,特别是在马尔可夫信息源上下文和隐马尔可夫模型中
。术语“维特比路径”和“维特比算法”也被用于寻找观察结果最有可能解释相关的动态规划算法。例如在统计句法分析中动态规划算法可以被用于发现最可能的上下文无关的派生(解析)的字符串,有时被称为“维特比分析”。
根据动态规划原理,最优路径具有这样的特性:如果最优路径在时刻t通过结点 ,那么这一路径从结点
到终点
的部分路径,对于从
到
的所有可能的部分路径来说,必须是最优的。
因为假如不是这样,那么从 到
就有另外一条更好的部分路径存在,如果把它和从
到达
的部分路径连接起来,就会形成一条比原来的路径更优的路径,这是矛盾的。
依据这个原理,我们只需要从时刻t=1开始,递推地计算在时刻t状态为i的各条部分路径的最大概率,直至得到时刻t=T状态为i的各条路径的最大概率。
时刻t=T的最大概率即为最优路径的概率 ,最优路径的终结点
也同时得到。之后,为了找到最优的路径的各个结点,从终结点
开始,由后向前逐步求得结点
,得到最优路径
,这就是维特比算法。
首先导入两个变量 和
,定义在时刻t状态为i的所有单个路径
中概率最大值为
由定义可得变量 的递推公式:
定义在时刻t状态为i的所有单个路径 中概率最大的路径的的t-1个结点为:
下面来看看算法的过程是什么样子的:
输入:模型 和观测
.
输出:最优路径 .
1.初始化
2.递推。对于t=2,3,4...,T:
3.终止。
4.最优路径回溯。对于t=T-1,T-2,....,1
求得最优路径为 。
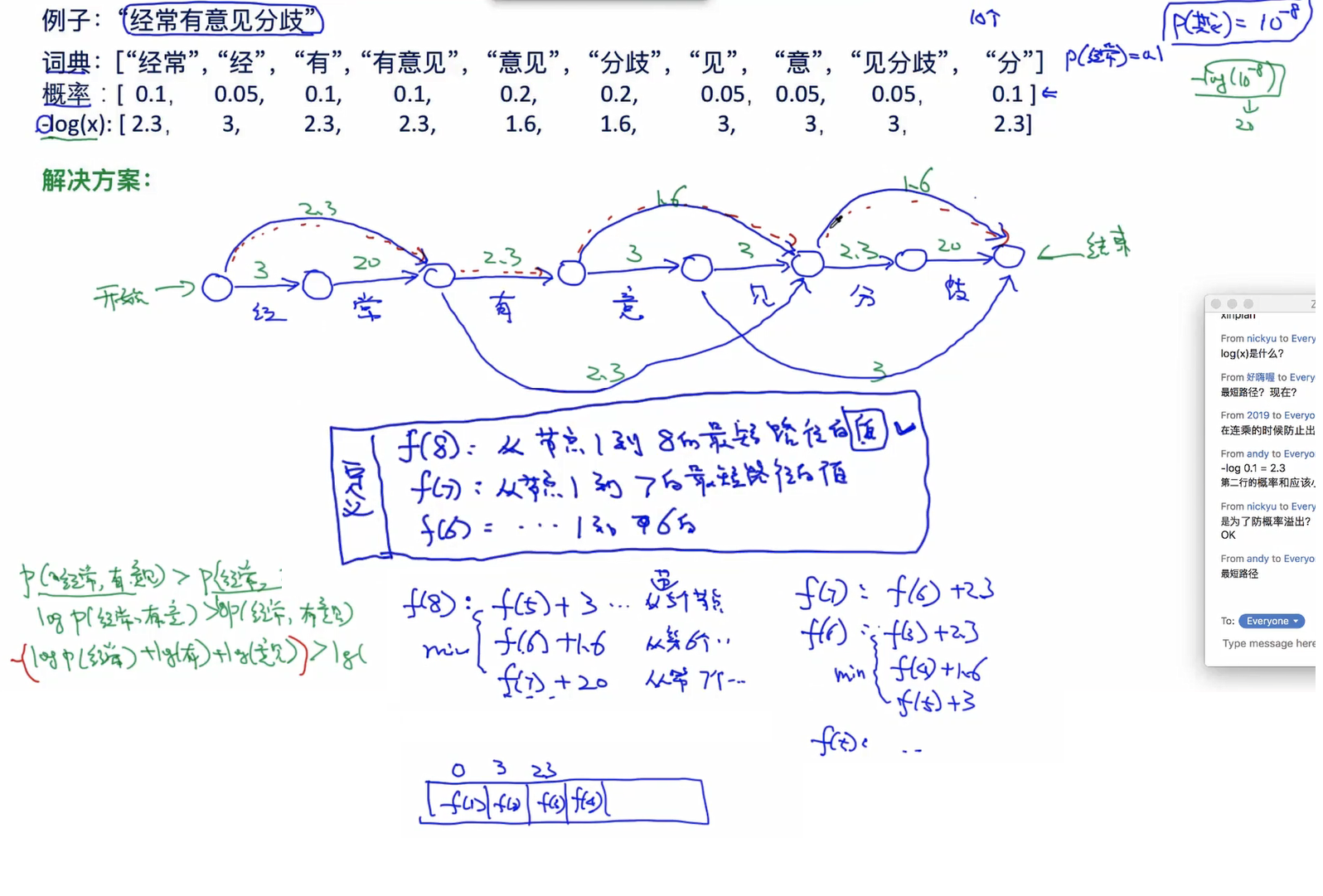
如果还是不太明白则可以从篱笆网络理解维特比算法:
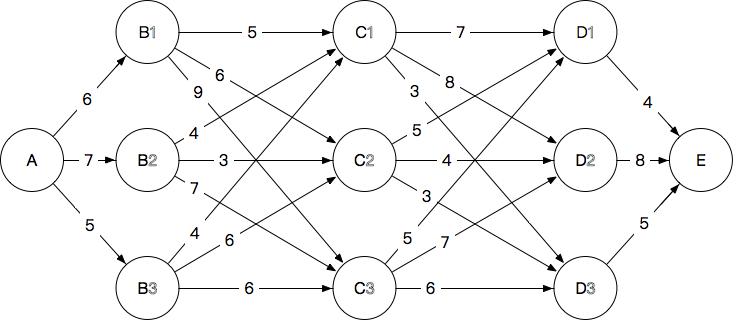
每条路径需要计算44次加法,一共3×3×3=273×3×3=27条路径共108次计算
如果我最终想要到达E这个节点,其实无论如何都是要经过D这一层的,那么要是我知道从A到D的每一个节点的最短路径长度。
1.A→B
6,7,5
2.A→B→C 我们确定到每一个C的节点,应该路过哪一个B:
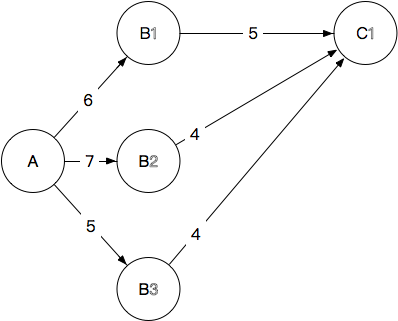
C1:6+5=11, 7+4=11, 5+4=9,最终选择A→B3→C1,抛弃其他到C1的路径,长度9
C2:12 ,10 ,11, 最终选择A→B2→C2,抛弃其他到C2的路径,长度10
C3:15,14,11,最终选择A→B3→C3,抛弃其他到C3的路径,长度11
3.A(→B)→C→D
我们确定到每一个D的节点,应该路过哪一个C

1.D_1:9+7=16,10+5=15,11+5=16,最终选择A→B2→C2→D1,抛弃其他到D1的路径,长度15
2.D_2:17,14,18,最终选择A→B2→C2→D2,抛弃其他到D2的路径,长度14
3.D_3:12,13,17,最终选择A→B3→C1→D3,抛弃其他到D3的路径,长度12
4.A(→B→C)→D→E
我们确定每一个D到最终节点E的路程
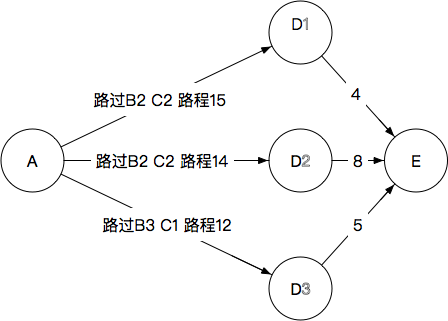
显然最后应该选择D3,完整路径为
A→B3→C1→D3→E
路程为17。抛弃其他所有路径。
从A到B有3条路径,每一条我们需要算到每一个C的最短距离:
所以是2(路径加法数)×3(A→B)×3(B→C),
只要我们确定了每一个到C的最短距离剩下的事情就可以从C开始考虑了:
每一个C需要确定到每一个D的最短距离,最终再加上D到E的距离就搞定了(2(路径加法数)×3(C个数)×3(D个数) 。
最终结果108==》18+18=36
如果换成是12层,每层最多13节点的话,每推一步的计算量最大规模在13^2(为了确定从哪一个B来到C,需要对每一个B到每一个C进行一次计算,上述计算每步是3^2=9次),而因为子问题都是一样的,所以增长是与网络长度成正比的:
推进12次也仅仅乘以12而已。当然计算的方式不可能像这样简单乘一乘就搞定,但是可以看得出要比穷举要简单得多了。
这又是DP算法。
而且维特比算法和HMM算法关系特别紧密。经过群友提示李航的书中HMM是由维特比算法求解的。
简单的回顾(我之前看过西瓜书了)
1.题目背景:
从前有个村儿,村里的人的身体情况只有两种可能:健康或者发烧。
假设这个村儿的人没有体温计或者百度这种神奇东西,他唯一判断他身体情况的途径就是到村头我的偶像金正月的小诊所询问。
月儿通过询问村民的感觉,判断她的病情,再假设村民只会回答正常、头晕或冷。
有一天村里奥巴驴就去月儿那去询问了。
第一天她告诉月儿她感觉正常。
第二天她告诉月儿感觉有点冷。
第三天她告诉月儿感觉有点头晕。
那么问题来了,月儿如何根据阿驴的描述的情况,推断出这三天中阿驴的一个身体状态呢?
为此月儿上百度搜 google ,一番狂搜,发现维特比算法正好能解决这个问题。月儿乐了。
2.已知情况:
隐含的身体状态 = { 健康 , 发烧 }
可观察的感觉状态 = { 正常 , 冷 , 头晕 }
月儿预判的阿驴身体状态的概率分布 = { 健康:0.6 , 发烧: 0.4 }
月儿认为的阿驴身体健康状态的转换概率分布 = {
健康->健康: 0.7 ,
健康->发烧: 0.3 ,
发烧->健康:0.4 ,
发烧->发烧: 0.6
}
月儿认为的在相应健康状况条件下,阿驴的感觉的概率分布 = {
健康,正常:0.5 ,冷 :0.4 ,头晕: 0.1 ;
发烧,正常:0.1 ,冷 :0.3 ,头晕: 0.6
}
阿驴连续三天的身体感觉依次是: 正常、冷、头晕 。
3.题目:
已知如上,求:阿驴这三天的身体健康状态变化的过程是怎么样的?
4.过程:
根据 Viterbi 理论,后一天的状态会依赖前一天的状态和当前的可观察的状态。那么只要根据第一天的正常状态依次推算找出到达第三天头晕状态的最大的概率,就可以知道这三天的身体变化情况。
传不了图片,悲剧了。。。
1.初始情况:
- P(健康) = 0.6,P(发烧)=0.4。
2.求第一天的身体情况:
计算在阿驴感觉正常的情况下最可能的身体状态。
- P(今天健康) = P(正常|健康)*P(健康|初始情况) = 0.5 * 0.6 = 0.3
- P(今天发烧) = P(正常|发烧)*P(发烧|初始情况) = 0.1 * 0.4 = 0.04
那么就可以认为第一天最可能的身体状态是:健康。
3.求第二天的身体状况:
计算在阿驴感觉冷的情况下最可能的身体状态。
那么第二天有四种情况,由于第一天的发烧或者健康转换到第二天的发烧或者健康。
- P(前一天发烧,今天发烧) = P(前一天发烧)*P(发烧->发烧)*P(冷|发烧) = 0.04 * 0.6 * 0.3 = 0.0072
- P(前一天发烧,今天健康) = P(前一天发烧)*P(发烧->健康)*P(冷|健康) = 0.04 * 0.4 * 0.4 = 0.0064
- P(前一天健康,今天健康) = P(前一天健康)*P(健康->健康)*P(冷|健康) = 0.3 * 0.7 * 0.4 = 0.084
- P(前一天健康,今天发烧) = P(前一天健康)*P(健康->发烧)*P(冷|发烧) = 0.3 * 0.3 *.03 = 0.027
那么可以认为,第二天最可能的状态是:健康。
4.求第三天的身体状态:
计算在阿驴感觉头晕的情况下最可能的身体状态。
- P(前一天发烧,今天发烧) = P(前一天发烧)*P(发烧->发烧)*P(头晕|发烧) = 0.027 * 0.6 * 0.6 = 0.00972
- P(前一天发烧,今天健康) = P(前一天发烧)*P(发烧->健康)*P(头晕|健康) = 0.027 * 0.4 * 0.1 = 0.00108
- P(前一天健康,今天健康) = P(前一天健康)*P(健康->健康)*P(头晕|健康) = 0.084 * 0.7 * 0.1 = 0.00588
- P(前一天健康,今天发烧) = P(前一天健康)*P(健康->发烧)*P(头晕|发烧) = 0.084 * 0.3 *0.6 = 0.01512
那么可以认为:第三天最可能的状态是发烧。
5.结论
根据如上计算。这样月儿断定,阿驴这三天身体变化的序列是:健康->健康->发烧。
这个算法大概就是通过已知的可以观察到的序列,和一些已知的状态转换之间的概率情况,通过综合状态之间的转移概率和前一个状态的情况计算出概率最大的状态转换路径,从而推断出隐含状态的序列的情况。


利用编辑距离可以判断两个字符串的相似程度,即从一个字符串到另一个字符串所需要的编辑次数,包括插入字符,删除字符及替换字符这三种操作。最小编辑距离即从一个字符串到另一个字符串所需要的最小编辑次数。

最小编辑距离同时被多个人独立发现,由Wagner和Fischer在1974年命名。让我们先定义两个字符串间的最小编辑距离。有两个字符串X和Y,X长度为n,Y长度为m。D[i, j] 为X[1..i]到Y[1.. j]的最小编辑距离。X[1..i]表示X的前i个字符,Y[1.. j]表示Y的前j个字符,D[n,m]为X和Y的最小编辑距离。
采用动态规划方法计算D[n,m], D[i,j]从小到大采用图3-3计算,del-cost表示删除操作的代价值,ins-cost表示插入操作的代价值,sub-cost表示替换操作的代价值,source表示原字符串,target表示转换的目标字符串。如果定义插入和删除的代价值为1,替换的代价值为2。
最小编辑距离计算:
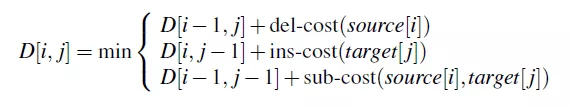
确代价值的最小编辑距离计算:

最小编辑距离算法总结如图3-5,图3-6列出了intention和execution字符串跟根据图3-5计算方法,算法的详细计算结果。












欧式距离并没有考虑到向量的方向性质,只考虑了scalar。
下面就是我们使用余弦相似度,查看文本相似距离。


那如何解决这种单词的重要性不一样的问题呢?
tf-idf:
TF,词频(term frequency),即一个单词在文档中出现的次数。一般来说,在某个文档中反复出现的单词,往往能够表征文档的主题信息,即TF值越大,越能代表文档所反映的内容,那么应该给予这个单词更大的权值。
IDF,逆文档频率(inverse document frequency),是一个词语普遍重要性的度量。词频因子是与文档密切相关的,说一个单词的TF值,指的是这个单词在某个文档中的出现次数,同一个单词在不同文档中TF值很可能不一样。而逆文档频率因子IDF则与此不同,它代表的是文档集合范围的一种全局因子。给定一个文档集合,那么每个单词的IDF值就唯一确定,跟具体的文档无关。所以IDF考虑的不是文档本身的特征,而是特征单词之间的相对重要性。

使用sklearn.feature_extraction.text 中的 CountVectorizer ==> TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer corpus = [ 'This is the first document.', 'This document is the second document.', 'And this is the third one.', 'Is this the first document?', ] vectorizer = CountVectorizer() # 根据语料计算词频矩阵 X = vectorizer.fit_transform(corpus) # 打印文档集合中所有单词 print(vectorizer.get_feature_names()) # 打印词频矩阵 print(X.toarray()) transformer = TfidfTransformer() # 根据词频矩阵计算TF-IDF值 tfidf = transformer.fit_transform(X) # 打印TF-IDF计算结果 print(tfidf.toarray())

使用sklearn.feature_extraction.text 中的 TfidfVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer corpus = [ 'This is the first document.', 'This document is the second document.', 'And this is the third one.', 'Is this the first document?', ] vectorizer = TfidfVectorizer() # 根据原始语料直接计算TF-IDF值 tfidf = vectorizer.fit_transform(corpus) # 打印文档集合中所有单词 print(vectorizer.get_feature_names()) # 打印TF-IDF计算结果 print(tfidf.toarray())

结果一致,一般直接使用 TfidfVectorizer求的。
不过问为什么tfidf这样表示,还是从信息路论的角度比较好解释。参考《数学之美》。




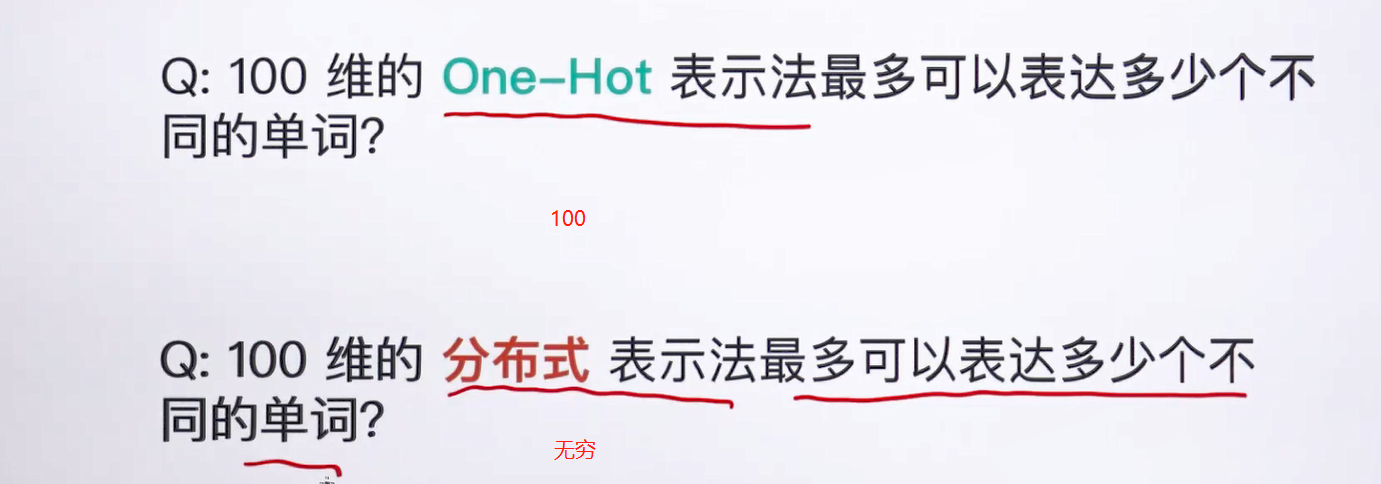
问题出现在单词的表示上,这种表示方法,不应该使用one-hot方法
另一个问题就是过于稀疏

下面使用词向量的方式