回归模型（二）逻辑回归

从线性回归到逻辑回归

最简单的回归是线性回归，在Andrew NG的讲义，有如图1.a所示，X为数据点——肿瘤的大小，Y为观测值——是否是恶性肿瘤。通过构建线性回归模型，如h_θ(x)所示，构建线性回归模型后，即可以根据肿瘤大小，预测是否为恶性肿瘤h_θ(x)≥.05为恶性，h_θ(x)<0.5为良性。

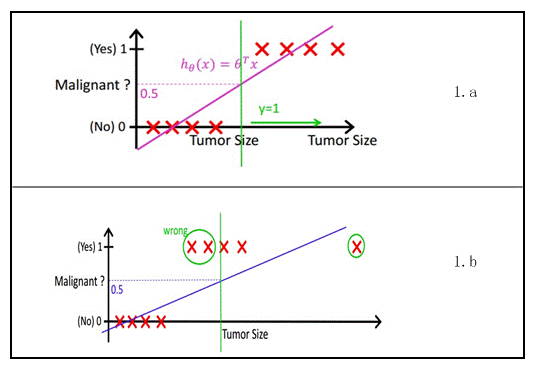
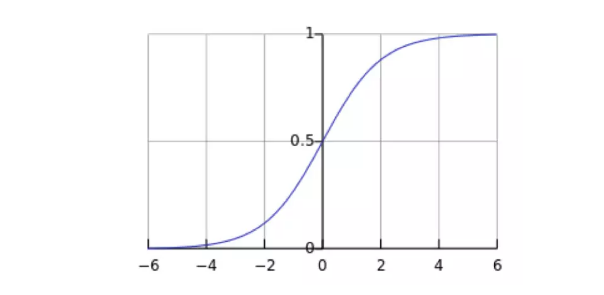
然而线性回归的鲁棒性很差，例如在图1.b的数据集上建立回归，因最右边噪点的存在，使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致，而分类范围，需要在[0,1]。逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型，其回归方程与回归曲线如图2所示。逻辑曲线在z=0时，十分敏感，在z>>0或z<<0处，都不敏感，将预测值限定为(0,1)。

分类问题

二分类问题就是给定的输入 $m{x}$ ，判断它的标签是A类还是类。二分类问题是最简单的分类问题。

预测一个用户是否点击特定的商品
判断用户的性别
预测用户是否会购买给定的品类
判断一条评论是正面的还是负面的

要解决这些问题，通常会用到一些已有的分类算法，比如逻辑回归，或者支持向量机。它们都属于有监督的学习，因此在使用这些算法之前，必须要先收集一批标注好的数据作为训练集。有些标注可以从log中拿到（用户的点击，购买），有些可以从用户填写的信息中获得（性别），也有一些可能需要人工标注（评论情感极性）。另一方面，知道了一个用户或者一条评论的标签后，我们还需要知道用什么样的特征去描述我们的数据，对用户来说，可以从用户的浏览记录和购买记录中获取相应的统计特征，而对于评论来说，最直接的则是文本特征。

但是我们拿得到的数据往往是连续的变量，输出的结果也是连续的变量。所以就考虑到下面的问题。

用连续的数值去预测离散的标签值

线性回归的输出是一个数值，而不是一个标签，显然不能直接解决二分类问题。那我如何改进我们的回归模型来预测标签呢？

感知机（Perceptron）模型：

一个最直观的办法就是设定一个阈值，比如0，如果我们预测的数值 y > 0 ，那么属于标签A，反之属于标签B。

基于概率的辑回归模型 (Logistics Regression)：

我们不去直接预测标签，而是去预测标签为A概率，我们知道概率是一个[0,1]区间的连续数值，那我们的输出的数值就是标签为A的概率。一般的如果标签为A的概率大于0.5，我们就认为它是A类，否则就是B类。

二分类模型评价

拿到数据的特征和标签后，就得到一组训练数据：

其中 xi 是一个 m 维的向量，Misplaced & ，y 在 {0, 1} 中取值。（本文用{1，0}表示正例和负例，后文沿用此定义。）

问题可以简化为，如何找到这样一个决策函数y∗=f(x)，它在未知数据集上能有足够好的表现。

逻辑回归推导

从线性回归到逻辑回归

线性回归的表达式： $f(m{x}) = m{w}^Tm{x} + b$ ，线性回归对于给定的输入 $m{x}$ ，输出的是一个数值 y ，因此它是一个解决回归问题的模型。

为了消除掉后面的常数项b，我们可以令 $egin{matrix} m{x}^{'} &= [ 1 & m{x}]^T end{matrix}$ ，同时 $egin{matrix} m{w}^{'} &= [ b & m{w}]^T end{matrix}$ ，也就是说给x多加一项而且值恒为1，这样b就到了w里面去了，直线方程可以化简成为：

$f(m{x'}) = m{w'}^Tm{x'}$ ，后面使用的 $m{w},m{x}$ 代指 $w',x'$ 。

概率是属于[0,1]区间。但是线性模型 $f(m{x}) = m{w}^Tm{x}$ 值域是 $(-infty,infty)$ 。所以不能直接基于线性模型建模。需要找到一个模型的值域刚好在[0,1]区间，同时要足够好用，sigmoid函数是不二之选。

它的表达式为： $sigma(x) =frac{1}{1+e^{-x}}$ 。

结合sigmoid函数，线性回归函数，把线性回归模型的输出作为sigmoid函数的输入。于是最后就变成了逻辑回归模型：

$y=sigma(f(m{x})) = sigma(m{w}^Tm{x})=frac{1}{1+e^{-m{w}^Tm{x}}}$

假设我们已经训练好了一组权值 $m{w}^T$ 。只要把我们需要预测的 $m{x}$ 代入到上面的方程，输出的y值就是这个标签为A的概率，我们就能够判断输入数据是属于哪个类别。

逻辑回归的损失函数（Loss Function）

损失函数就是用来衡量模型的输出与真实输出的差别。

假设只有两个标签1和0， $y_n in{0, 1}$ 。我们把采集到的任何一组样本看做一个事件的话，那么这个事件发生的概率假设为p。我们的模型y的值等于标签为1的概率也就是p。

$P_{y=1}=frac{1}{1+e^{-m{w}^Tm{x}}} = p$ 。因为标签不是1就是0，因此标签为0的概率就是： $P_{y=0} = 1-p$ 。

我们把单个样本看做一个事件，那么这个事件发生的概率就是： $P(y|m{x})=left{ egin{aligned} p, y=1 \ 1-p,y=0 end{aligned} ight.$ 这个函数不方便计算，它等价于: $P(y_i|m{x}_i) = p^{y_i}(1-p)^{1-{y_i}}$ 。

解释下这个函数的含义，我们采集到了一个样本 $(m{x_i},y_i)$ 。对这个样本，它的标签是 $y_i$ 的概率是 $p^{y_i}(1-p)^{1-{y_i}}$ 。（当y=1，结果是p；当y=0，结果是1-p）。

如果我们采集到了一组数据一共N个， ${(m{x}_1,y_1),(m{x}_2,y_2),(m{x}_3,y_3)...(m{x}_N,y_N)}$ ，这个合成在一起的合事件发生的总概率怎么求呢？其实就是将每一个样本发生的概率相乘就可以了，即采集到这组样本的概率：

$egin{aligned} P_{总} &= P(y_1|m{x}_1)P(y_2|m{x}_2)P(y_3|m{x}_3)....P(y_N|m{x}_N) \ &= prod_{n=1}^{N}p^{y_n}(1-p)^{1-y_n} end{aligned}$ 。注意 $P_{总 }$ 是一个函数，并且未知的量只有 $m{w}$ （在p里面）。

通过两边取对数来把连乘变成连加的形式，即：

$egin{aligned} F(m{w})=ln(P_{总} ) &= ln(prod_{n=1}^{N}p^{y_n}(1-p)^{1-y_n} ) \ &= sum_{n=1}^{N}ln (p^{y_n}(1-p)^{1-y_n}) \ &= sum_{n=1}^{N}(y_n ln (p) + (1-y_n)ln(1-p)) end{aligned}$ 其中， $p = frac{1}{1+e^{-m{w}^Tm{x}}}$ ，这个函数 $F(m{w})$ 又叫做它的损失函数。

损失函数可以理解成衡量我们当前的模型的输出结果，跟实际的输出结果之间的差距的一种函数。这里的损失函数的值等于事件发生的总概率，我们希望它越大越好。但是跟损失的含义有点儿违背，因此也可以在前面取个负号。

使用最大似然估计MLE(Maximum Likelihood Estimation)估计参数 $m{w}$ 跟b的值呢，损失函数 $F（m{w}）$ 是正比于总概率 $P_{总}$ 的，而 $F（m{w}）$ 又只有一个变量 $m{w}$ 。也就是说，通过改变 $m{w}$ 的值，就能得到不同的总概率值 $P_{总}$ 。那么当我们选取的某个 $m{w}^*$ 刚好使得总概率 $P_{总}$ 取得最大值的时候。我们就认为这个 $m{w}^*$ 就是我们要求得的 $m{w}$ 的值，这就是最大似然估计的思想。

现在问题变成了找到一个 $m{w}^*$ ，使得我们的总事件发生的概率，即损失函数 $F（m{w}）$ 取得最大值，数学表达就是：

$m{w^*} = argmax_{w}F(m{w}) = -argmin_{w}F(m{w})$

求取 $F（m{w}）$ 的梯度 $abla F（m{w}）$ ？

p是一个关于变量 $m{w}$ 的函数，我们对p求导，通过链式求导法则，可得：

$egin{aligned} p' = f'(m{w})&= (frac{1}{1+e^{-m{w}^Tm{x}}} )' \ &= -frac{1}{ (1+e^{-m{w}^Tm{x}} )^2} · ( 1+e^{-m{w}^Tm{x}})' \ &= -frac{1}{ (1+e^{-m{w}^Tm{x}} )^2} · e^{-m{w}^Tm{x}} · (-m{w}^Tm{x})' \ &= -frac{1}{ (1+e^{-m{w}^Tm{x}} )^2} · e^{-m{w}^Tm{x}} · (-m{x} ) \ &= frac{e^{-m{w}^Tm{x}} }{ (1+e^{-m{w}^Tm{x}} )^2} · m{x} \ &= frac{1}{ 1+e^{-m{w}^Tm{x}} } · frac{e^{-m{w}^Tm{x}} }{ 1+e^{-m{w}^Tm{x}} } · m{x} \ &= p(1-p)m{x} end{aligned}$

$1-p$ 的值： $1-p=frac{e^{-m{w}^Tm{x}} }{ 1+e^{-m{w}^Tm{x}} }$ ，我们也对1-p进行如上的求导。

最终求得： $p' = p(1-p)m{x}$ 和 $(1-p)' = -p(1-p)m{x}$ 。

正式开始对 $F(m{w})$ 求导，求导的时候请始终记住，我们的变量只有 $m{w}$ ，其他的什么 $y_n,m{x}_n$ 都是已知的，看做常数。

$egin{aligned} abla F（m{w}）& = abla （ sum_{n=1}^{N}(y_n ln (p) + (1-y_n)ln(1-p)) ）\ &= sum ( y_n ln'(p) + (1-y_n) ln'(1-p)) \ &= sum( (y_n frac{1}{p}p')+(1-y_n)frac{1}{1-p}(1-p)') \ &= sum(y_n(1-p)m{x}_n - (1-y_n)pm{x}_n) \ &= sum_{n=1}^{N}{(y_n-p)m{x}_n} end{aligned}$

所以，梯度 $abla F（m{w}）$ 的表达式最终为：

$egin{aligned} abla F（m{w}）&= sum_{n=1}^{N}{(y_n-p)m{x}_n} end{aligned}$

把p再展开，即：

$egin{aligned} abla F（m{w}）&= sum_{n=1}^{N}{(y_n- frac{1}{1+e^{-m{w}^Tm{x}_n}} )m{x}_n} end{aligned}$

梯度下降法（GD）与随机梯度下降法（SGD）

为什么可以用梯度下降法？

因为逻辑回归的损失函数L是一个连续的凸函数（conveniently convex）。这样的函数的特征是，它只会有一个全局最优的点，不存在局部最优。

在逻辑回归里面就不存在局部最优，因为它的损失函数的良好特性，导致它并不会有好几个局部最优。

当我们的GD跟SGD收敛以后，我们得到的极值点一定就是全局最优的点，因此我们可以放心地用GD跟SGD来求解。

已经解出了损失函数 $F（m{w}）$ 在任意 $m{w}$ 处的梯度 $abla F（m{w}）$ ，我们现在要求损失函数取最大值时候的 $m{w^*}$ 的值： $m{w^*} = argmax_{w}F(m{w})$

梯度下降法(Gradient Descent)，可以用来解决这个问题。

核心思想就是先随便初始化一个 $m{w}_0$ ，然后给定一个步长 $eta$ ，通过不断地修改 $m{w}_{t+1}$ <- $m{w}_{t}$ ，从而最后靠近到达取得最大值的点，即不断进行下面的迭代过程，直到达到指定次数，或者梯度等于0为止。

$m{w}_{t+1} = m{w}_t + eta abla F（m{w}）$

随机梯度下降法（Stochastic Gradient Descent），如果我们能够在每次更新过程中，加入一点点噪声扰动，可能会更加快速地逼近最优值。

在SGD中，我们不直接使用 $abla F（m{w}）$ ，而是采用另一个输出为随机变量的替代函数 $G(m{w})$ : $m{w}_{t+1} = m{w}_t + eta G(m{w})$

当然，这个替代函数 $G(m{w})$ 需要满足它的期望值等于 $abla F（m{w}）$ ，相当于这个函数围绕着 $abla F（m{w}）$ 的输出值随机波动。

在GD求导每次都用到了所有的样本点，从1一直到N都参与梯度计算。

$egin{aligned} abla F（m{w}）&= sum_{n=1}^{N}{(y_n- frac{1}{1+e^{-m{w}^Tm{x}_n}} )m{x}_n} end{aligned}$

在SGD中，我们每次只要均匀地、随机选取其中一个样本 $(m{x_i},y_i)$ ,用它代表整体样本，即把它的值乘以N，就相当于获得了梯度的无偏估计值，即 $E(G(m{w})) = abla F(m{w})$ ，因此SGD的更新公式为：

$m{w}_{t+1} = m{w}_t + eta N {(y_n- frac{1}{1+e^{-m{w}^Tm{x}_n}} )m{x}_n}$

这样我们前面的求和就没有了，同时 $eta N$ 都是常数， $N$ 的值刚好可以并入 $eta$ 当中,因此SGD的迭代更新公式为：

$m{w}_{t+1} = m{w}_t + eta {(y_n- frac{1}{1+e^{-m{w}^Tm{x}_n}} )m{x}_n}$ ，其中 $(m{x_i},y_i)$ 是对所有样本随机抽样的一个结果。

加入正则项的损失函数

正则化是用来防止模型过拟合的过程，常用的有L1正则化和L2正则化两种选项，分别通过在损失函数后加上参数向
量的L1范式和L2范式的倍数来实现。这个增加的范式，被称为“正则项”，也被称为"惩罚项"。损失函数改变，基
于损失函数的最优化来求解的参数取值必然改变，我们以此来调节模型拟合的程度。其中L1范式表现为参数向量中
的每个参数的绝对值之和，L2范数表现为参数向量中的每个参数的平方和的开方值。

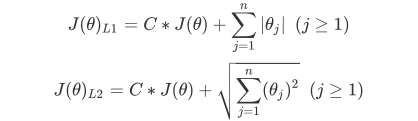
加入正则的损失函数，C是用来控制正则化程度的超参数，n是方程中特征的总数，也是方程中参
数的总数，j代表每个参数。j要大于等于1，是因为我们的参数向量中，第一个参数是，是我们的截
距，它通常是不参与正则化的。

penalty	可以输入"l1"或"l2"来指定使用哪一种正则化方式，不填写默认"l2"。注意，若选择"l1"正则化，参数solver仅能够使用求解方式”liblinear"和"saga“，若使用“l2”正则化，参数solver中所有的求解方式都可以使用。
C	C正则化强度的倒数，必须是一个大于0的浮点数，不填写默认1.0，即默认正则项与损失函数的比值是1：1。C越小，损失函数会越小，模型对损失函数的惩罚越重，正则化的效力越强，参数 Θ会逐渐被压缩得越来越小

sklearn实战

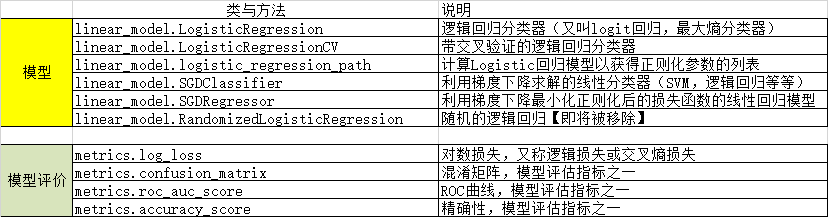
LogisticRegression详解

class sklearn.linear_model.LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, 
　　　　　　　　　　　　　　　　　　　　　　　　　　　　random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)

参数介绍

求解器

梯度下降法，只是求解逻辑回归参数的一种方法，sklearn提供了更多选择，让我们可以使用不同的求解器来计算逻辑回归。

求解器的选择，由参数"solver"控制，共有五种选择。其中“liblinear”是二分类专用，也是现在的默认求解器。

数据证明：

莺尾花数据集多分类问题

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression as LR
iris = load_iris()
for multi_class in ('multinomial', 'ovr'):
    for solver in ('lbfgs','newton-cg','sag','saga'):
        clf = LR(solver=solver, max_iter=100, random_state=42,multi_class=multi_class).fit(iris.data, iris.target)

        print("training score : %.3f (%s+%s)" % (clf.score(iris.data, iris.target),multi_class,solver))

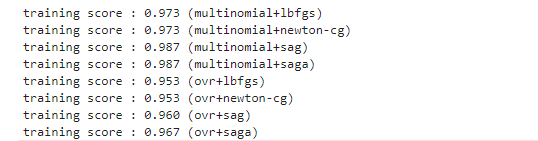
乳腺癌数据实战

乳腺癌数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score#精确性分数
 
data = load_breast_cancer()#乳腺癌数据集
X = data.data
y = data.target
 
dir(data)
data.feature_names

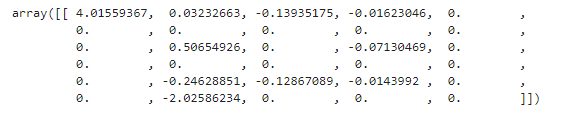
逻辑回归的重要属性coef_

X.data.shape#(569, 30)
 
lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
 
#逻辑回归的重要属性coef_，查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_
# (lrl1.coef_ != 0).sum(axis=1)#array([10])    30个特征中有10个特征的系数不为0

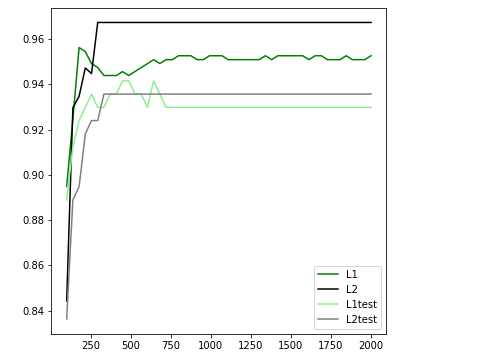
对参数C对的调优

l1 = []
l2 = []
l1test = []
l2test = []
 
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
 
for i in np.linspace(0.05,1.5,19):
    lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
    lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
    
    lrl1 = lrl1.fit(Xtrain,Ytrain)
    l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
    l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
 
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]    
 
plt.figure(figsize=(6,6))
for i in range(len(graph)):
    plt.plot(np.linspace(0.05,1.5,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示，右下角
plt.show()

对参数max_iter的调

from sklearn.model_selection import cross_val_score

l1 = []
l2 = []
l1test = []
l2test = []
 
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
 
for i in np.linspace(1,200,50):
    lrl1 = LR(penalty="l1",solver="liblinear",C=0.75,max_iter= i )
    lrl2 = LR(penalty="l2",solver="liblinear",C=0.75,max_iter= i )
    
    lrl1 = lrl1.fit(Xtrain,Ytrain)
    l1.append(cross_val_score(lrl1,data.data,data.target,cv=10).mean())
    l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
 
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]    
 
plt.figure(figsize=(6,6))
for i in range(len(graph)):
    plt.plot(np.linspace(100,2000,50),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示，右下角
plt.show()

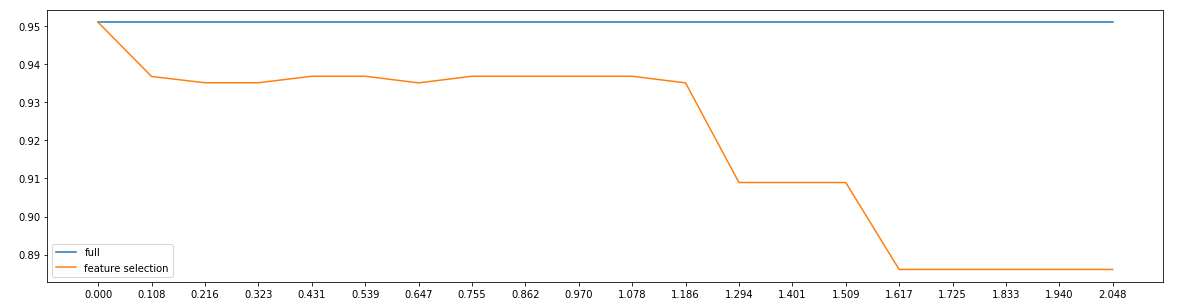
特征筛选

fullx = []
fsx = []
 
threshold = np.linspace(0,abs((LR_.fit(data.data,data.target).coef_)).max(),20)
 
#全特征
cross_val_score_value=cross_val_score(LR_,data.data,data.target,cv=5).mean()
#特征筛选
for i in threshold:
    X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(data.data,data.target)
    fullx.append(cross_val_score_value)
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=5).mean())

    
plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label="full")
plt.plot(threshold,fsx,label="feature selection")
plt.xticks(threshold)
plt.legend()
plt.show()

相关阅读:
vim 高级功能
 Vim高手，从来不用鼠标2——替换、撤销、缩进、查找
 Vim高手，从来不用鼠标
 zookeeper的leader选举机制个人总结
 【JVM】GC之垃圾收集算法
 【软件工程】常见的几种软件过程模型的比较
 【设计模式】适配器模式
 【计算机网络】网络的硬件构成要素
 【计算机网络】ISO/OSI 网络体系结构
 【Spring Cloud】Spring Cloud Config 实现分布式配置中心
原文地址：https://www.cnblogs.com/wqbin/p/11637901.html

回归模型（二） 逻辑回归

从线性回归到逻辑回归

分类问题

用连续的数值去预测离散的标签值

二分类模型评价

逻辑回归推导

从线性回归到逻辑回归

逻辑回归的损失函数（Loss Function）

梯度下降法（GD）与随机梯度下降法（SGD）

加入正则项的损失函数

sklearn实战

LogisticRegression详解

求解器

乳腺癌数据实战

回归模型（二）逻辑回归