题目大意:
有一棵N个结点树和N头奶牛,一开始所有奶牛都在一号结点,奶牛们将按从编号1到编号N的顺序依次前往自己的目的地,求每头奶牛在去往自己目的地的途中将会经过多少已经有奶牛的结点。
题解:
可以发现,每一头奶牛到达目的地后,都只会对还未到达目的地的奶牛中,目的地在它目的地子树中的奶牛的答案产生贡献。
比如说在下面这棵树中,一头奶牛到达了图中深色结点,那么在还未到达目的地的奶牛中,只有目的地在深色结点子树中的奶牛才会由深色结点对答案产生贡献。
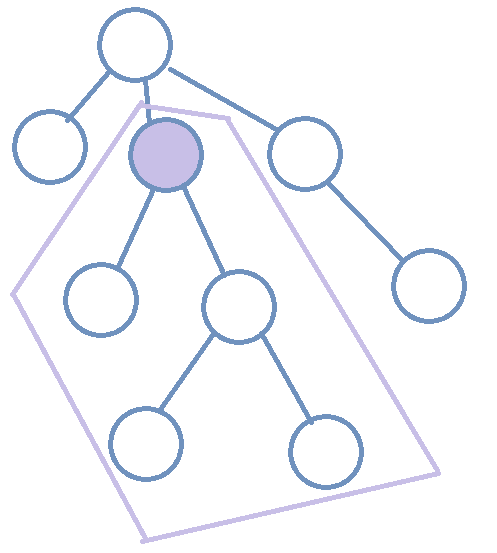
所以,我们可以在每头奶牛到达目的地后,将其目的地所在结点的子树中每一个结点的权值都加上一,询问时输出该奶牛目的地所在结点的权值即可。
由于每一次的修改操作都是在一棵子树内进行的,所以考虑用dfs序给结点编号(因为每棵子树中结点的dfs序都一定是连续的一段),再用线段树进行维护就好。
代码:
#include<iostream> #include<cstdio> using namespace std; struct edge { int last; int end; }e[200005]; int ne=0,idx=0,dfn[100005],note[100005],size[100005],tree[400005],lazy[400005]; void make_edge(int u,int v) { ne++; e[ne].last=note[u]; e[ne].end=v; note[u]=ne; } void dfs(int x,int fx) { dfn[x]=++idx;//用dfs序给结点编号 size[x]=1; for(int i=note[x];i;i=e[i].last) if(e[i].end!=fx) { dfs(e[i].end,x);//继续dfs //计算每个结点的子树大小,用于计算此结点的子树中最大的dfs序是多少,便于操作 size[x]+=size[e[i].end]; } } //线段树板子 void add_node(int p,int l,int r,int k) { tree[p]+=(r-l+1)*k; lazy[p]+=k; } void clean_lazy(int p,int l,int r) { int mid=(l+r)>>1; add_node((p<<1),l,mid,lazy[p]); add_node((p<<1)+1,mid+1,r,lazy[p]); lazy[p]=0; } void add(int p,int l,int r,int x,int y) { if(x>y) return; if(l==x&&r==y) { add_node(p,l,r,1); return; } clean_lazy(p,l,r); int mid=(l+r)>>1; if(y<=mid) add((p<<1),l,mid,x,y); else if(x>mid) add((p<<1)+1,mid+1,r,x,y); else add((p<<1),l,mid,x,mid),add((p<<1)+1,mid+1,r,mid+1,y); } int ask(int p,int l,int r,int x) { if(l==r) return tree[p]; clean_lazy(p,l,r); int mid=(l+r)>>1; if(x<=mid) return ask((p<<1),l,mid,x); return ask((p<<1)+1,mid+1,r,x); } int main() { int n=0; scanf("%d",&n); for(int i=1;i<n;i++) { int u=0,v=0; scanf("%d%d",&u,&v); make_edge(u,v); make_edge(v,u); } dfs(1,0); for(int i=1;i<=n;i++) { int x=0; scanf("%d",&x); printf("%d ",ask(1,1,n,dfn[x]));//直接输出目的地所在的权值 add(1,1,n,dfn[x]+1,dfn[x]+size[x]-1);//给当前目的地所在结点的子树中所有结点的权值都加1 } return 0; }