二叉堆的解释
(动态选择优先级最高的任务执行)
堆,又称为优先队列。虽然名为优先队列,但堆并不是队列。堆和队列是两种不同的数据结构,堆是树态的,队列是线性的。在队列中,我们可以向队列添加元素,取出的时候是按照进入队列的先后顺序取出元素的,先进先出;而在堆中,却不是按照元素添加的先后顺序,而是按照元素的优先级取出元素。
所以二叉堆是为了找出最大或最小而生的,“大”和“小”并不是传统意义上的小大,而是优先级的高低。二叉堆分为最大堆和最小堆,最大堆的顶点可以看作是优先级最高的也可以看作是优先级最低的,最小堆也是如此。
二叉堆是一种完全二叉树,因为完全二叉树的特性普遍使用数组结构是非常好用的,所以性注定了二叉堆的存储形式只能是数组或者动态数组(长度可变)。
二叉堆最主要的操作是两个,siftUp上浮和siftDown下沉,来保证二叉堆的性质:
1.父节点的键值总是优先于任何一个子节点的键值;
2.左右子树都是以一个二叉堆。
展示最大堆
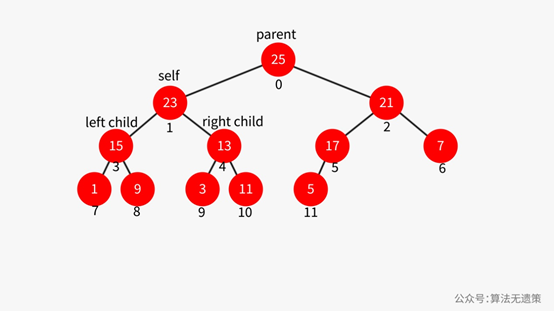
用数组存储二叉堆,堆的顶点下标可以从0开始也可以从1开始。看上面图中,以self为参照物,self下标的变量为i:
parent(i) = (i - 1) / 2;
leftChild(i) = 2 * i + 1;
rightChild(i) = leftChild(i) + 1 = 2 * i + 2;
如果是堆顶下标从1开始:
parent(i) = i / 2;
leftChild = 2 * i;
rightChild = 2 * i + 1;
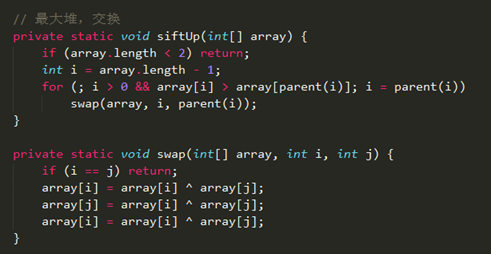
向堆中添加元素siftUp
二叉堆的节点添加,是在数组的最末尾插入新节点的,然后进行自下而上调整子节点和父节点,不满足二叉堆性质则交换,直到当前子树满足二叉堆的性质。如果可以为了减少交换次数的话,可以单向复制,使得添加的节点插入到合适的位置。
动画siftUp
Code:单向复制

Code:交换法
取出堆中最大的元素siftDown
取出堆中最大的元素其实是取出根节点,这个下沉的操作很有意思了。它有两方面的下沉:一方面是将根节点下沉到数组末尾,然后数组长度假象性减一下;另一方面是将交换后的根节点和左右子树的根节点作比较,不满足堆性质的则交换。
动画siftDown
Code:siftDown单向复制
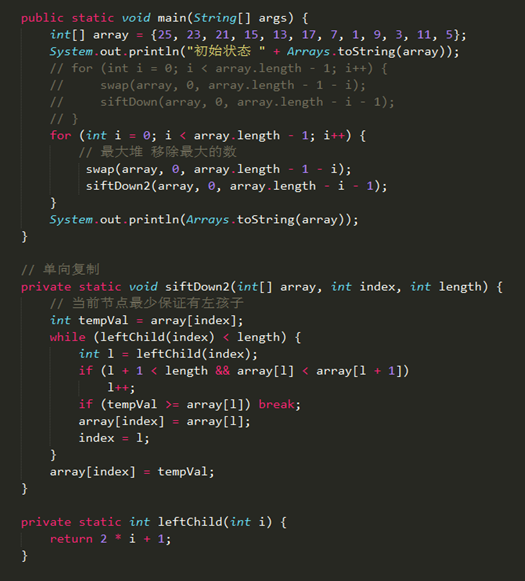
Code:siftDown交换法
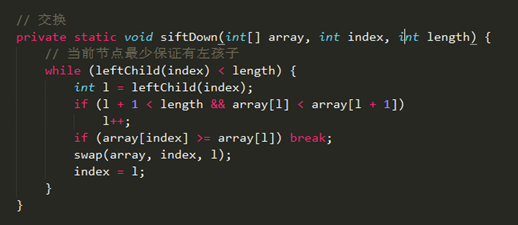
构建二叉堆
构建二叉堆其实是一个一个子树的下沉操作,将无序的完全二叉树调整为二叉堆。所以它必须从满足高度为2的子树根节点开始,即非叶子节点,然后自底向上对每一个子树执行siftDown操作,直到完成二叉堆化。
动画:构建二叉堆
Code
