冒泡排序

冒牌排序算法时间复杂度最坏的情况是,最好的,说明冒泡排序是可以优化的,就看你有没有去发现。
冒泡排序算法的过程是两个元素比较的大小,是典型的交换排序算法。快速排序算法和鸡尾酒排序算法也属于交换排序。我这篇介绍完之后下一篇章会介绍快速排序和鸡尾酒排序。所以要自己学会关注哦,给这个公众号标上星标,不会迷失下一篇好文。
排序方法
比较相邻的元素,判断是否符合要求,如果不符合就交换位置来达到排序的目的。
对每一对相邻元素做相同的工作,从开始第一对到结尾的最后一对,一次遍历之后,最后一个元素是最大(小)的数。
第二次遍历重复以上操作,因为最后一个元素已经确定位置,减少一次计算。以此类推。

示例
通过一个示例来理解基本的冒泡排序算法,假设当前我们有一个数组a,里面元素是:5,6,1,7,2,4,3
初始状态
视频动画
Code

Result
初始状态[5, 6, 1, 7, 2, 4, 3]
发生交换[5, 1, 6, 7, 2, 4, 3]
发生交换[5, 1, 6, 2, 7, 4, 3]
发生交换[5, 1, 6, 2, 4, 7, 3]
发生交换[5, 1, 6, 2, 4, 3, 7]
1次遍历:[5, 1, 6, 2, 4, 3, 7]
发生交换[1, 5, 6, 2, 4, 3, 7]
发生交换[1, 5, 2, 6, 4, 3, 7]
发生交换[1, 5, 2, 4, 6, 3, 7]
发生交换[1, 5, 2, 4, 3, 6, 7]
2次遍历:[1, 5, 2, 4, 3, 6, 7]
发生交换[1, 2, 5, 4, 3, 6, 7]
发生交换[1, 2, 4, 5, 3, 6, 7]
发生交换[1, 2, 4, 3, 5, 6, 7]
3次遍历:[1, 2, 4, 3, 5, 6, 7]
发生交换[1, 2, 3, 4, 5, 6, 7]
4次遍历:[1, 2, 3, 4, 5, 6, 7]
5次遍历:[1, 2, 3, 4, 5, 6, 7]
6次遍历:[1, 2, 3, 4, 5, 6, 7]
优化
可以发现,我们到第4次遍历的时候,发现已经排序完了,但是代码还是会继续判断是否符合要求。
仔细看看,第4次遍历之前还有一次元数位置交换,第5次遍历之前已经没有了交换。
所以我们可以设置一个标志位,用来表示当前i+1次是否还有交换,如果有就进行下一趟遍历,如果没有,则说明当前数组已经排完序,没有再进行比较的判断了。
Code
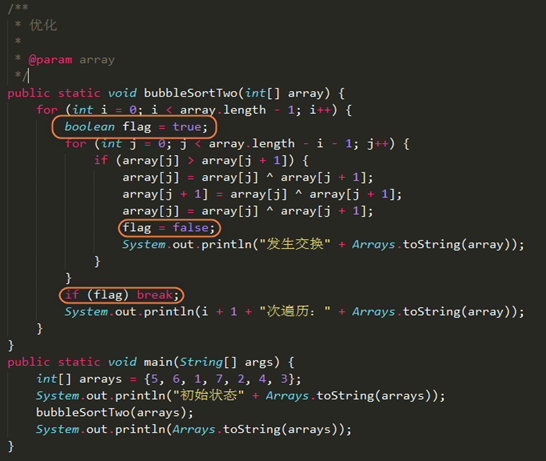
Result
初始状态[5, 6, 1, 7, 2, 4, 3]
发生交换[5, 1, 6, 7, 2, 4, 3]
发生交换[5, 1, 6, 2, 7, 4, 3]
发生交换[5, 1, 6, 2, 4, 7, 3]
发生交换[5, 1, 6, 2, 4, 3, 7]
1次遍历:[5, 1, 6, 2, 4, 3, 7]
发生交换[1, 5, 6, 2, 4, 3, 7]
发生交换[1, 5, 2, 6, 4, 3, 7]
发生交换[1, 5, 2, 4, 6, 3, 7]
发生交换[1, 5, 2, 4, 3, 6, 7]
2次遍历:[1, 5, 2, 4, 3, 6, 7]
发生交换[1, 2, 5, 4, 3, 6, 7]
发生交换[1, 2, 4, 5, 3, 6, 7]
发生交换[1, 2, 4, 3, 5, 6, 7]
3次遍历:[1, 2, 4, 3, 5, 6, 7]
发生交换[1, 2, 3, 4, 5, 6, 7]
4次遍历:[1, 2, 3, 4, 5, 6, 7]
好了这是第一次的优化,减少了计算次数。看上面的执行过程,你觉得还有什么办法使得时间复杂度尽可能少一点呢?
优化,还能再继续优化
我觉得还能再继续优化,为了更直白一点,这次我们换一个数组,数组元素为:4, 3, 2, 1, 5, 6, 7
Code

Result
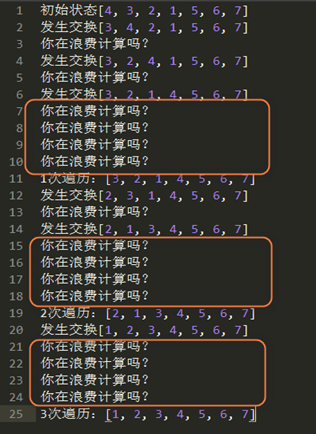
看到上面的结果可以看出一个问题,里面的for循环明明已经归位了,又增加了不必要的计算次数。问题是在于j < array.length – i – 1。
我们可以这样解决,进行第1次遍历之前,记录交换元素的最后一个位置lastPostion。交换后的元素后一个肯定要比前面一个元素大,lastPostion就记录前面一个元素就可以了。
进行一次遍历之后,lastPostion的记录有了,里面的for循环进行下标0到lastPostion的数组就可以了,lastPostion后面的一串数组由于前面第一次循环验证过了,没有任何交换的元素 ,说明也是排好序的。
视频动画
Code

Result
