两个坐标点之间的距离小于或大于10（最优算法）

朋友跟我分享的某大厂面试题：

两个坐标点之间的距离小于或大于某个值。最简单的算法，勾股定理，distance = (x1-x2)的平方 + (y1-y2)的平方，最后开根号。还有没有效率更高的算法啊？百度没找到答案，我写下自己的，如果大家有好的想法，记得给我留言啊啊啊~~

我的算法思想是：先求出弧度，再用cos把10映射到x轴的长度，最后再比较。

执行1千万次的结果是方法2效率高。

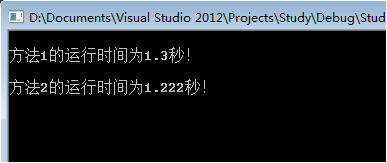
直接上代码吧。

#include <iostream>
#include <time.h>
#include <math.h> 
//坐标点1
double nX1 = -3;double nY1 = -3;
//坐标点2
double nX2 = 3;double nY2 = 3;
//方法1勾股定理
bool CheckNear1(int nTarLen)
{
	int nLen = sqrt((pow((nX1-nX2), 2) + pow((nY1-nY2), 2)));
	return nTarLen > nLen;
}
//方法2利用弧度算出给定值对应的直角边长度
bool CheckNear2(int nTarLen)
{
	int nSubX = abs(nX1-nX2);
	int nLen = nTarLen*cos(atan(nSubX/(nY1-nY2)));
	return nLen > nSubX;
}
int main()
{
	clock_t start,finish;
	start=clock();
	for (int i = 0;i<10000000;++i)
	{
		CheckNear1(10);
	}
	finish=clock();
	cout<<"
方法1的运行时间为"<<(double)(finish-start)/CLOCKS_PER_SEC<<"秒！"<<endl;

	start=clock();
	for (int i = 0;i<10000000;++i)
	{
		CheckNear2(10);
	}
	finish=clock();
	cout<<"
方法2的运行时间为"<<(double)(finish-start)/CLOCKS_PER_SEC<<"秒！"<<endl;
	return 0;
}