（板子）并查集（递归+循环）

并查集板子的luogu传送门

并查集是一个十分实用的算法，经常可以实现类似图论中寻找强联通的效果。

其实，常规并查集的思想十分简单：给每个数据维护一个数组 f，初始化都是这个数据自己。然后，

如果要讲两个数据合并，我们只需要将其中一个数据i的 f[i] 更改为另一个数据j的 f[j]，就相当于讲这两个数据进行了“合并”。

这个时候，我们就将f[j]（即j）作为这个集合的“老大”，以后加进来的元素都以它为元首进行集合判断。

接下来考虑如何实现：

首先，我们要求算法可以找到这个集合的“老大”。于是很轻易的设计出了以下递归算法：

int find (int k){
    if(f[k] == k)return k;
    else return find(f[k]);
}
//在引用处，加入元素x到元素y所在集合操作：
f[x] = find(y);

算法要求是实现了，可是时间效率呢？答案是：很容易被卡。

どうして？（皇家翻译：为什么？）

因为有时候，我们可能会出现下面这种情况：(懒，用了洛谷的图)

                                 

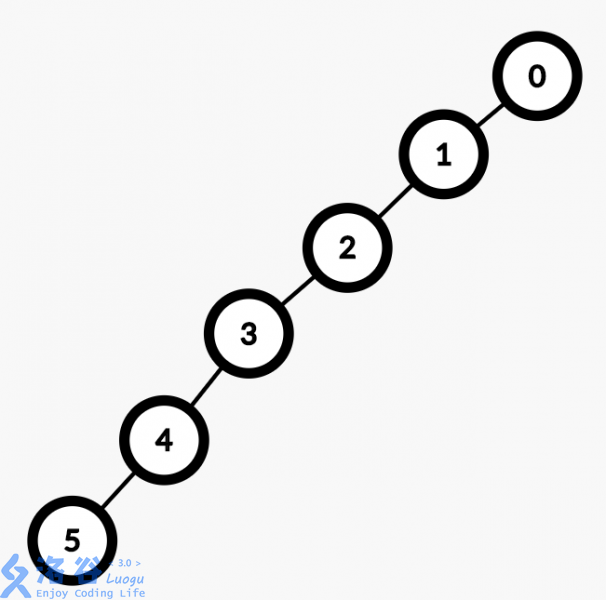
没错，有些数据可以把你的时间复杂度卡为O(N),效率极低。

だから，（皇家翻译：So，）

如何解决？

其实很简单：

在找老大的时候把路径上的小弟的 f 也顺便直接改成老大，这样查询集合的时候就可以近似做到O（1）的复杂度。

int find(int x){
    if(x == f[x]) return x;
    else return f[x] = find(f[x]); // 在这里更新路径上的小弟
}

 其实就是把图变成下面这样：

                                              

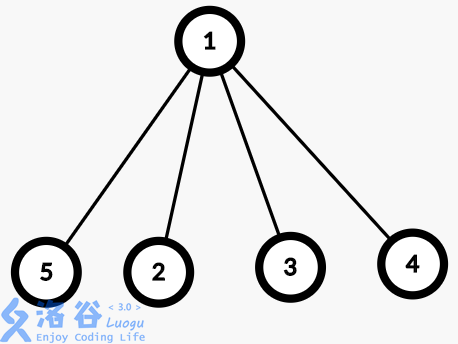
通过以上这些操作，并查集就完成了。

p.s:并查集也有循环版的，效率可能会比递归的快, 这里就不多说了：

int find(int x){
    while(x!=fa[x]) x = fa[x] = fa[fa[x]];
    return x;
}

End：luogu的AC模板代码贴一下呗：

#include<bits/stdc++.h>
using namespace std;

int n,m,f[66666];
int Find(int x){
    while(x != f[x])x = f[x] = f[f[x]]
    return x;
}

void unit(int x,int y){
    x = Find(x);
    y = Find(y);
    if(x != y)f[x] = y;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n; i++)f[i] = i;
    for(int i = 1;i <= m; i++){
        int x,y,z;
        scanf("%d",&z);
        if(z == 1){
            cin >> x >> y;
            unit(x,y);//x的目前老大的老大变成了y最终的老大 
        }
        else if(z == 2){
            scanf("%d%d",&x,&y);
            if(Find(x) == Find(y))printf("Y
");
            else printf("N
");
        }
    }
    return 0;
}