Car的旅行路线
问题描述
又到暑假了,住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场,分别位于一个矩形的四个顶点上,同一个城市中两个机场之间有一 条笔直的高速铁路,第I个城市中高速铁路了的单位里程价格为Ti,任意两个不同城市的机场之间均有航线,所有航线单位里程的价格均为t。
那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题,于是她来向你请教。
找出一条从城市A到B的旅游路线,出发和到达城市中的机场可以任意选取,要求总的花费最少。
那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题,于是她来向你请教。
找出一条从城市A到B的旅游路线,出发和到达城市中的机场可以任意选取,要求总的花费最少。
输入格式
数据的第一行有四个正整数s,t,A,B。
S表示城市的个数,t表示飞机单位里程的价格,A,B分别为城市A,B的序号,(1<=A,B<=S)。
接下来有S行,其中第I行均有7个正整数xi1,yi1,xi2,yi2,xi3,yi3,Ti,这当中的(xi1,yi1),(xi2,yi2),(xi3,yi3)分别是第I个城市中任意三个机场的坐标,Tl为第I个城市高速铁路单位里程的价格。
S表示城市的个数,t表示飞机单位里程的价格,A,B分别为城市A,B的序号,(1<=A,B<=S)。
接下来有S行,其中第I行均有7个正整数xi1,yi1,xi2,yi2,xi3,yi3,Ti,这当中的(xi1,yi1),(xi2,yi2),(xi3,yi3)分别是第I个城市中任意三个机场的坐标,Tl为第I个城市高速铁路单位里程的价格。
输出格式
共有n行,每行一个数据对应测试数据,保留一位小数。
样例输入
1
1 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3
1 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3
样例输出
47.5
数据规模和约定
对于100%的数据, 1 <= n <= 10, 1 <= S <= 100, 1 <= A, B <= S.
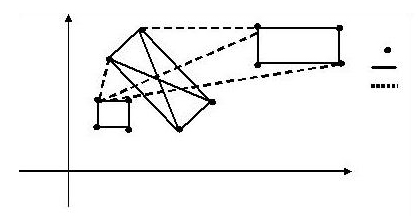
题目中让我们求出从城市A到城市B的最小花费。
不难看出,这是一道最短路的问题,将最小花费看作每条边的长度,用SPFA(Floyd)跑最短路即可。
然而,每个城市有4个机场,去每个机场的花费都不一样。因此,考虑将一个城市拆分成4个点,在存点的时候储存下城市编号(类似强联通编号),进行特判就好了。
如果是同一个城市的,边长以为铁路票价 * dis, 不同城市则为 plane * dis。
答案即为终点四个机场中最小的。
(勾股定理好评!)
#include <bits/stdc++.h> using namespace std; #define N 401 #define isdigit(c) ((c)>='0'&&(c)<='9') #define min(a,b) ((a)>(b)?(b):(a)) /*比 STL 快?*/ inline int read(){ int x = 0, s = 1; char c = getchar(); while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); } while(isdigit(c)){ x = (x << 1) + (x << 3) + (c ^ '0'); c = getchar(); } return x * s; } struct node{//存每个机场的信息 int x, y; int city, price; } t[N << 2]; double d[N << 2]; int n, pla_pri, s, ht; inline int square(int x){ return x * x; } inline int dis(int a, int b){//暂时先不开根号,使用起来方便一些 return square(t[a].x - t[b].x) + square(t[a].y - t[b].y); //编号机场的距离 } inline void get4(int n1,int n2,int n3){ int x4, y4; int x1 = t[n1].x, y1 = t[n1].y, x2 = t[n2].x, y2 = t[n2].y, x3 = t[n3].x, y3 = t[n3].y; int ab = dis(n1, n2); int ac = dis(n1, n3); int bc = dis(n2, n3); if(ab == ac + bc) x4 = x1 + x2 - x3, y4 = y1 + y2 - y3;//勾股定理,求出第四个点 else if(ac == ab + bc) x4 = x1 + x3 - x2, y4 = y1 + y3 - y2; else if(bc == ac + ab) x4 = x2 + x3 - x1, y4 = y2 + y3 - y1; t[n3+1].x = x4, t[n3+1].y = y4; /* printf("x1:%d y1: %d x2: %d y2: %d x3: %d y3: %d x4: %d y4: %d ", x1,y1,x2,y2,x3,y3,x4,y4); 分段检查程序可以防止写完之后 Debug 两小时 */ return ; } void init(){ int cac_city = 0; for(int i = 1;i <= (n << 2); i += 4){ t[i].x = read(), t[i].y = read(); t[i+1].x = read(), t[i+1].y = read(); t[i+2].x = read(), t[i+2].y = read(); t[i].price = t[i+1].price = t[i+2].price = t[i+3].price = read();//把价格记录下来 t[i].city = t[i+1].city = t[i+2].city = t[i+3].city = ++cac_city;//城市记录下来 get4(i, i+1, i+2);//寻找第四个点 } return ; } queue <int> q; bool vis[N << 2]; void spfa(){ /*时刻不忘 n 是4倍!!不然玄学错误!!*/ for(int i = 1;i <= (n << 2); i++) d[i] = 99999999.99; for(int i = 4 * (s - 1) + 1;i <= 4 * (s - 1) + 4; i++){//都能作为起点,所以4个点全部推进去 vis[i] = 1; q.push(i); d[i] = 0; } while(!q.empty()){//SPFA int now = q.front();q.pop(); vis[now] = 0; for(int i = 1;i <= (n << 2); i++){//反正全部有连边,直接 for 循环不香吗 if(i == now)continue; double cost; if(t[i].city == t[now].city){//如果在同一个城市 cost = t[i].price * (double)sqrt((double)dis(i, now)); } else cost = pla_pri * (double)sqrt((double)dis(i, now));//连边的价值(距离) if(d[i] > d[now] + cost){ d[i] = d[now] + cost; if(!vis[i]){ vis[i] = 1; q.push(i); } } } } return ; } int main(){ // freopen("hh.txt", "r", stdin); int T = read(); while(T--){ n = read(), pla_pri = read(), s = read(), ht = read(); if(s == ht){ //这里用SPFA可以不特判,但是如果用Floyd就要特判了 (初始化成了极大值) puts("0.0"); continue; } init(); spfa(); double ans = ~0u >> 1; for(int i = 4 * (ht - 1) + 1;i <= 4 * (ht - 1) + 1 + 3; i++) ans = min(d[i], ans);//答案为终点四个机场里面最小的 printf("%.1lf ", ans); } return 0; }