（转）模型视图变换时，法线向量要乘模型视图矩阵的逆转置矩阵

转自：http://blog.csdn.net/christina123y/article/details/5963679

在计算机图形学中，只要是变换，无论平移，旋转，缩放，都是乘一个矩阵。
在模型视图变换时，顶点乘模型视图变换矩阵，而顶点对应的顶点法线向量（或其他的法线向量）则要乘模型视图矩阵的逆转置矩阵。
顶点和法线都是向量，他们的区别是什么？无非顶点是<x, y, z>表示缺省的<x, y, z, 1>，而法线向量是<x, y, z>表示缺省的<x, y, z, 0>。法线向量只能保证方向的一致性，而不能保证位置的一致性，所以，所有法线线向量必须以面的形式进行变换，如下：

Transforming Planes

If we have a plane vector n = [a, b, c, d] which describes a plane then for any point p = [x, y, z, 1] in that plane the follow equation holds:

n p^t = ax + by + cz + d = 0

If for a point p on the plane, we apply an invertible transformation R to get the transformed point p₁, then the plane vector n₁ of the transformed plane is given by applying a corresponding transformation Q to the original plane vector n where Q is unknown.

p₁^t = R p^t 
n₁^t = Q n^t  ==> n₁ = (Q n^t)^t  ==> n₁ = n Q^t

We can solve for Q by using the resulting plane equation:

n₁ p₁^t = 0

Begin by substituting for n₁ and p₁:

n Q^t R p^t  = 0

If Q^t R = E then n Q^t R p^t = n E p^t = n p^t  = 0 which is given.

所以， Q^t R = E
Q^t = R^-1
Q = (R^-1)^t

Substituting Q back into our plane vector transformation equation we get:

n₁^t = Q n^t   = (R^-1)^t n^t

下面是一个网友的解释，http://blog.csdn.net/christina123y/article/details/5963679

许多计算都在眼睛坐标系中完成，一个常用的就是光照需要在这个空间中实现，因为眼睛位置决定了光照效果，否则的话，很难实现镜面光。因此我们需要将法线坐标转换到眼睛坐标系中。在OpenGL ES 2.0中，将一个顶点转换至眼睛坐标系中，通过：

vertexEyeSpace = view_Matrix * rm_vertex;

那为什么我们不能像法线向量一样做同样的工作呢？首先法线向量是3个floats的向量，而modelView矩阵是4X4的矩阵。这可以通过以下代码来实现：

normalEyeSpace = vec3(view_Matrix * vec4(rm_Normal, 0.0));

它只可用于一些环境中，不能用于所有，但是上面存在一个潜在的问题：

首先看看顶点和法线向量的区别是什么：

    顶点是(x,y,z)表示缺省的向量(x,y,z,1)；而法线向量是一个方向性向量，没有固定的点。因为法线向量可由法线上两个固定顶点(x1,y1,z1,1), (x2,y2,z2,1)相减得到。因此，从这点就可以看到顶点与法线向量不同，也就造成了不现的变换。法线向量只能保证方向性的一致，不能保证位置性的一致。

潜在的问题是：

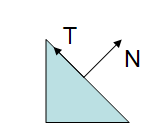
在上图我们看到一个三角形, 有一个法线向量和切线向量. 接下来的图显示当一个观察矩阵缩放的时候所显示的情景。

如果我们还是调用上面的代码的话：

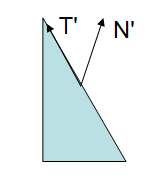
注意: 当观察矩阵各方向尺寸不一致时,应当预先保存法线的方向, 虽然法线的长度会变化,但是单元化很易修复
在上图, 观察矩阵影响到所有的顶点以及法线. 很明显这个结果是错误的. 法线并不垂直于切线。

所以现在我们得知并不能将观察矩阵应用于所有的法线. 所以我们应当应用怎样的矩阵呢?

注意到T*N = 0. 所以在视觉空间中, 两者还应当是垂直的, 保证转换后的T'*N' = 0.
假设矩阵G是转换法线N的矩阵.T则乘观察矩阵左上的3*3矩阵M(T是一个向量, 令w为0).式子如下:

点积可以转换成向量积, 如下


由于N"T = 0, 所以我们猜想
 (I为单位矩阵)
所以


因此gl_NormalMatrix等于M的逆矩阵的倒置矩阵

在本文的开始曾说模型观察矩阵作用于法线向量有时候也有效, 这是因为观察矩阵为正交矩阵, 即

正交矩阵 ---- 任意列/行向量都为单元长度向量. 并相互垂直.
这意味着任意两个向量乘以该向量, 向量间的角度不会发生任何变化.

如果我们仅仅在观察矩阵进行旋转或者移动,我们的当前模型矩阵仍为正交矩阵.
即我们只用glRotate和glTranslate命令,而不用glScale命令.
注意: 我们glLookAt产生的观察模型矩阵也是正交矩阵.

1、平移矩阵是有效的，不是因为平移矩阵的正交性[平移矩阵不是正交阵]。是因为两个原因：

1）、平移矩阵对法向量无效，因为它是向量，不是点

设有两个点的齐次坐标为：v1'(x1, y1, z1, 1); v2'(x2, y2, z2, 1)

然后这两点的直线的法向量为：n'(nx, ny, nz, 0)；注意最后一个0

移动a、b、c的平移矩阵为：T(a, b, c) =

1 0 0 a

0 1 0 b

0 0 1 c

0 0 0 1

可以验证:

T * v1' = (x1+a, y1+b, z1+c, 1)
T * v2' = (x2+a, y2+b, z2+c, 1)
但是：T * n' = (nx, ny, nz, 0)，所以得到平移变换对向量无效（这也符合常识）

2）、v1', v2'变换后的点如上所示，则：它们代表直线的向量还是和原来一样，v12' =(x2 - x1, y2 - y1, z2 - z1, 0)，然后：v12' * n'还是等于0；

2、同样道理，缩放矩阵也不是正交矩阵，但是缩放分两种，一种是均匀缩放，一种是非均匀缩放，对于均匀缩放，也是可以用点变换矩阵来做的，原理如下：

均匀缩放矩阵S，三个轴的缩放系数皆为a, S(a) =

a 0 0 0

0 a 0 0

0 0 a 0

0 0 0 1

所以：

S * v1' = (x1*a, y1*a, z1*a ,1)

S * v2' = (x2*a, y2*a, z2*a ,1)

S * n' = (nx*a, ny*a, nz*a ,0)

所以变换后的线向量为：v12 = (a*(x1-x2), a*(y1-y2), a*(z1-z2), 0)
所以变换后的法向和v12点乘时候可以把共用系数a抽出来，就变成了a^2乘以原来的乘积，还是0

至于非均匀缩放，是不能有这种结果的，所以不能用这种办法了。

3、至于文中的最后一句：“注意: 我们glLookAt产生的观察矩阵也是正交矩阵“，其实也不一定是，原因是因为:相机操作除了旋转到正确的轴之外，还有平移到世界原点，回到1，平移矩阵不是正交阵，所以结果不一定是正交的，不过如果相机位置本来就设在原点，那观察矩阵就肯定是正交的。

如果相机只是改变方向，那观察矩阵就是正交的。但世界矩阵如果包含平移和缩放的话就不是正交的。因此，模型矩阵大部分情况下不是正交的，除非相机和模型只改变方向的情况下是正交的。

因此，，如果M是正交的话，那么 

总是，在模型视图变换时，顶点乘模型视图变换矩阵M，而顶点对应的顶点法线向量（或其他的法线向量）则要乘模型视图矩阵的逆转置矩阵 (M^-1)^t