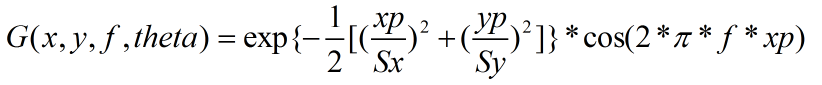Gabor变化属于加窗傅里叶变换,Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。Gabor函数与人眼的生物作用相仿,所以经常用于纹理识别上,并取得了较好的效果。
二维Gobor滤波函数:
其中:
xp = x*cos(theta)+y*sin(theta)
yp=y*cos(theta)-x*sin(theta)
| mean(平均值) | Con(对比度) | Ent(熵) | |
| theta=pi/10 | 0.0043 | 1.6111 | 0.4046 |
| theta=pi/4 | 0.0042 | 1.5869 | 0.3623 |
熵反映了图像的能量,当滤波器的方向和图像纹理方向越吻合,输出图像的能量越大。这证明了Gabor函数可以捕捉到相当多的纹理信息,具有极佳的空间特征。