线性模型
线性模型试图学得一个通过属性的线性组合来进行预测的函数。形如：
1、线性回归
2、多分类学习
3、逻辑回归（LR）
4、类别不均衡问题
一、线性回归
讲解线性回归之前，先要了解回归和分类的区别，简单来说，回归要做的就是一个连续的预测值，分类是一个离散的预测值。线性回归试图学的一个线性模型以尽可能准确地预测。
- 对于单变量线性回归
输入的属性值为只有一个，则函数为F（x）= w*x + b,其中f(x)约等于真实值y，为什么是约等于？
看一个例子：
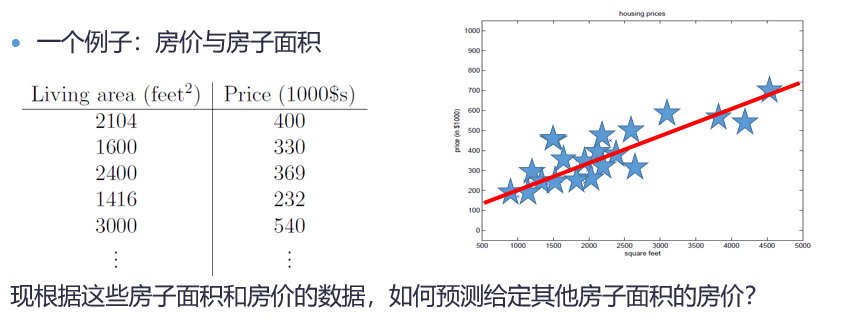
其中，蓝色星星为给定的数据，红色线为拟合后求出的线性方程，我们可以发现，我们要做的是使所有点到这条直线的距离和最短，以此来构造损失函数进行迭代求最优解。所以线性只是拟合了数据的分布趋势，并不是真正预测出实际值。这就是为什么是约等于。
那么如何来确定方程中的W和b？我们使用均方误差来构造损失函数，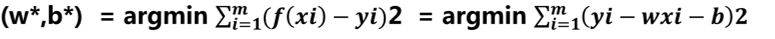
，均方误差的几何意义对应了常用的欧几里得距离。基于均方误差最小化来进行模型求解的方法称为最小二乘法。在线性回归中，最小二乘法就是试图找到一条直线，使得所有样本到直线上的欧式距离之和最小。
求解W和b的过程称为线性回归模型的最小二乘法“参数估计”。我们将损失函数分别对W和b求偏导，然后令偏导等于0，进行求解。
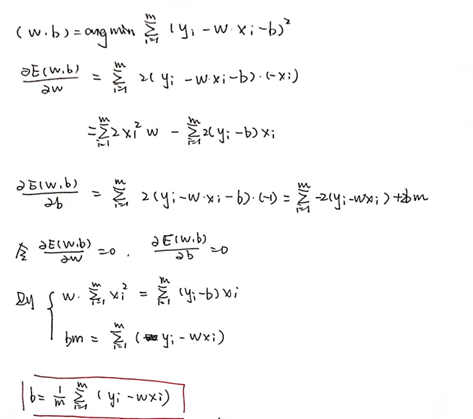
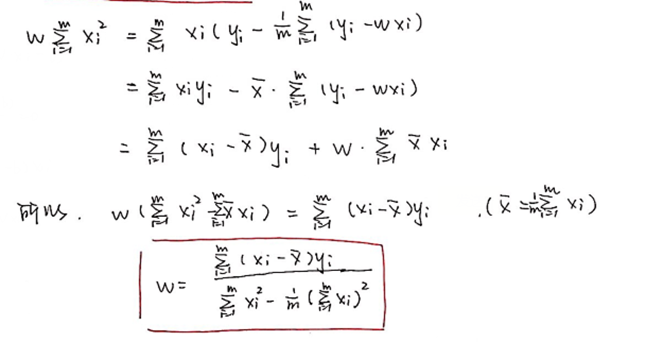
- 多分类学习
现实中常遇到多分类学习任务，我们使用一些基本策略的，利用二分类学习器来解决多分类问题（OVO,OVR,MVM）。
1、OvO
2、OvR
一个例子：
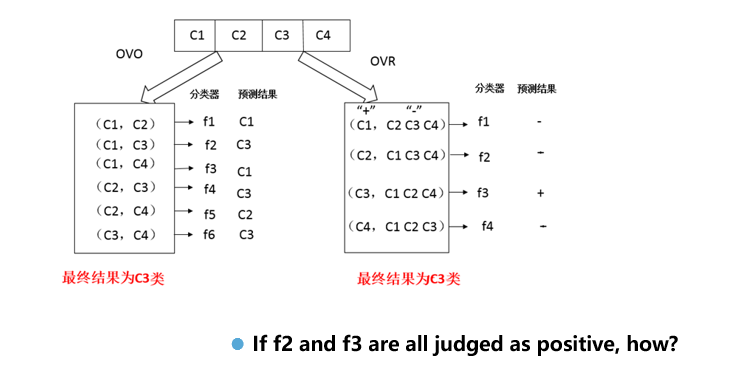
3、MvM
为解决上述判定结果相同的问题，提出MVM拆分策略。
二、逻辑回归
上节介绍了使用线性模型进行回归学习，但若要做分类任务怎么办？我们可以模拟预测值逼近y的衍生物，比如，假设我们认为输出的y值是指在指数尺度上的变换，那么我们的线性函数应为：ln(y) = wx+b，但实质上已是在求取输入空间到输出空间的非线性函数映射。这样得到的模型：y = g(wx+b)称为广义线性模型。
同理，逻辑回归的实质为用线性回归模型的预测结果去逼近真实标记的对数几率。运用广义线性模型把函数值映射在0-1之间。
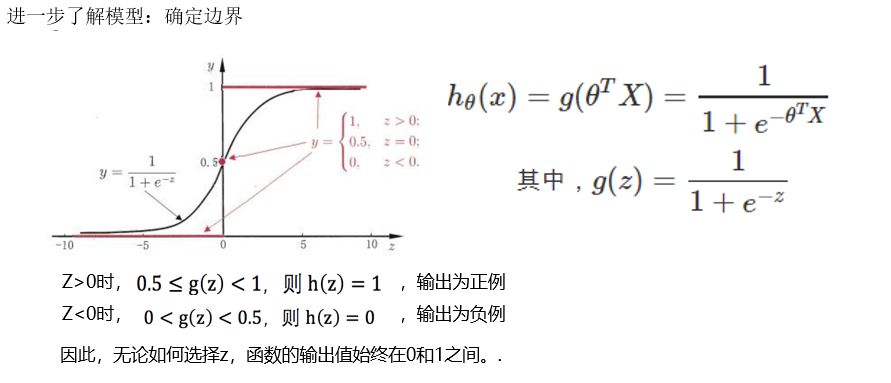
下面就是逻辑回归函数sigmod的推导过程。
三、类别不平衡问题
类别不平衡是指分类任务中不同类别的训练样例数目差别很大的情况。解决类别不平衡问题的方法是“再缩放”。
1、下采样
直接对训练集里的负样例进行下采样，即取出一些负样例，是正负平衡。
2、上采样
通过训练集的正样例进行插值产生额外的正样例。如果简单地对初始正样例进行重复，会导致过拟合。