数组
@(数据结构与算法)
数组
一种线性表数据结构。它用一组连续的内存管空间,开存储一组具有相同类型的数据。
-
线性表:数据排成一条线一样的结构。
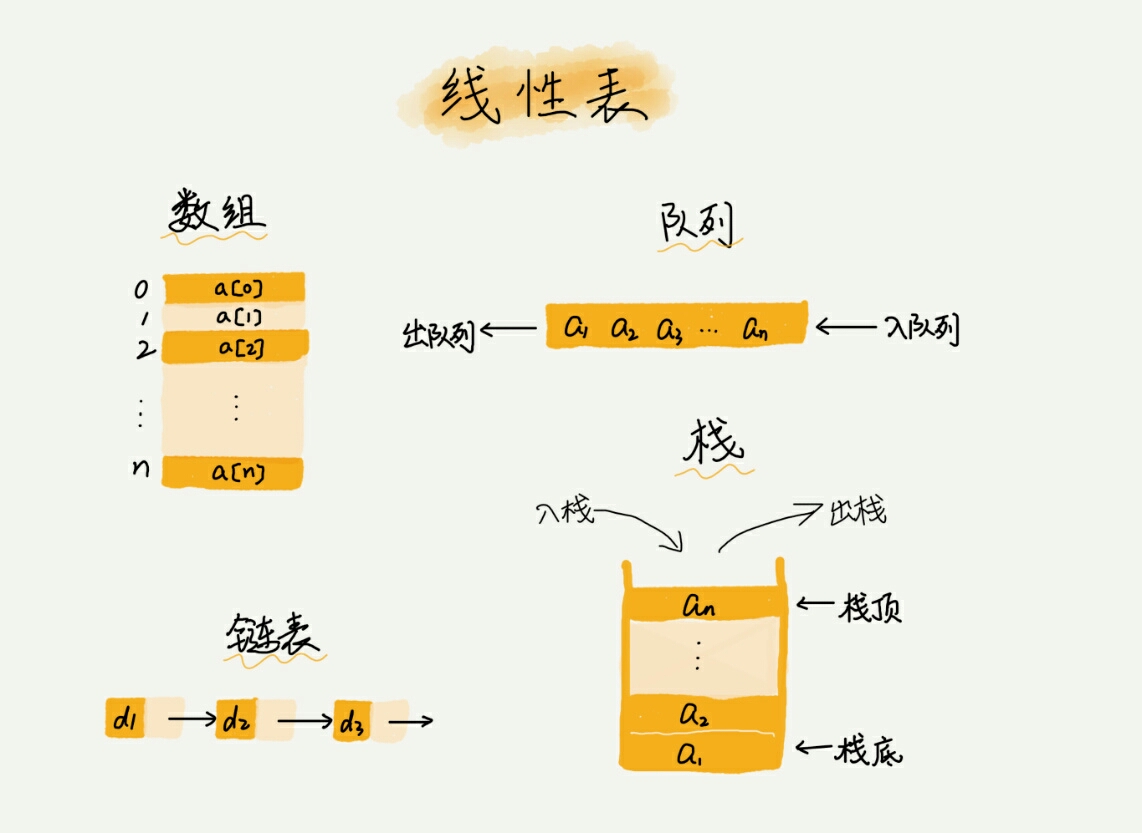
-
非线性表: 数据之间不是简单的前后关系。

数组的特性
随机访问。随机访问的缺点:如果要想在数组中删除、插入一个数据,为了保证连续性,就需要做大量的数据搬移工作。
数组访问的原理
一个长度为 10 的 int 类形的数组 int[] a = new int[10] ,计算机给数组 a[10] 分配了一块连续内存空间 1000 ~ 1039 , 内存块的首地址为 base_address = 1000.
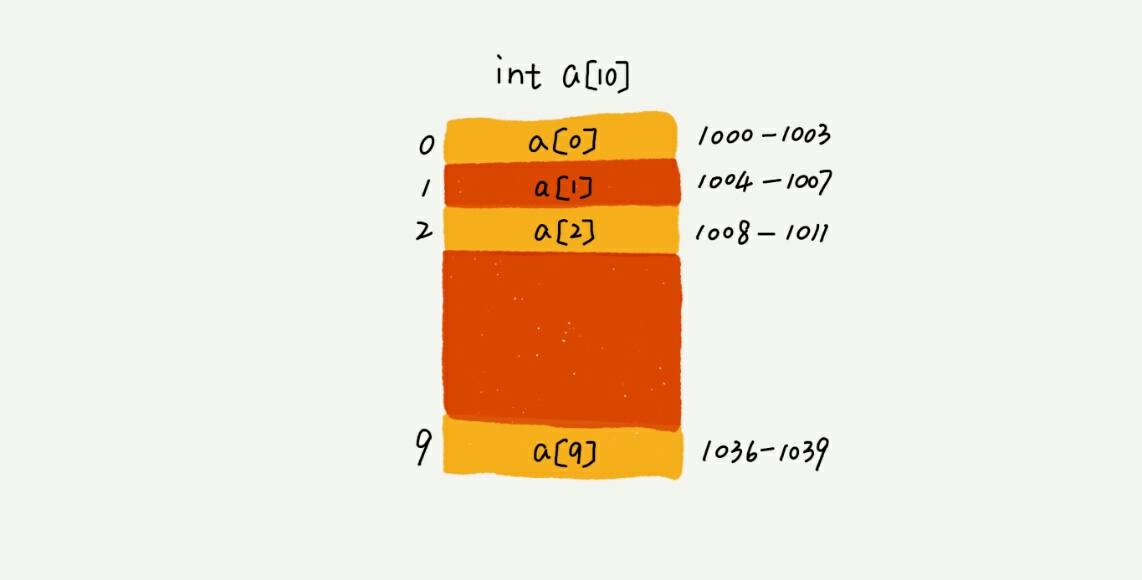
计算机会给每个内存单元分配一个地址,计算机通过地址来访问内存中的数据。当计算机需要访问内存中的数据时,会首先它通过公式计算出该元素存储的内存位置。
a[i]_address = base_address + i * data_type_size
其中 data_type_size 表示数组中每个元素的大小。int 类型数据的大小为 4 个字节。
数组和链表的区别:数组支持随机访问,根据下标随机访问的时间复杂度为 O(1) ,链表适合插入、删除,时间复杂度为 O(1)。
数组低效的 “插入” 和 “删除”
如果需要在数组中的第 k 个位置插入数据,则需要将 k ~ n 这部分的元素都顺序的往后挪一位,时间复杂度为 O(n)。
改进:
- 如果数组是无序的,只是被当做存储数据的集合。那么可以直接将第 k 位的数据搬移到数组元素的最后,把新的元素直接放入第 k 个位置,此时时间复杂度将为 O(1)。
如果要删除第 k 个位置的数据,为了内存的连续性,就需要搬移数据,时间复杂度为 O(n) 。
改进:
- 在某些实际场景,我们并不一定非得追求数组中数据的连续性。如果将多次删除操作集中在一起执行,删除的效率会更高。
例子;
- 数组 a[10] 中存储了 8 个元素:a,b,c,d,e,f,g,h。现在需要依次删除 a,b,c 三个元素。为避免其他几个元素被搬移三次,可以先记录下已经删除的数据。每次的删除操作并不真正的搬移数据,只是记录数据已经被删除。当数组没有更多空间存储数据时,我们在触发执行一次真正的删除操作。
参考自:极客时间《数据结构与算法之美 》专栏