复杂度分析(上)
@(数据结构与算法)
- 数据结构与算法本质上是解决程序运行速度快和存储空间省的问题,所以需要通过一个指标,即时间、空间复杂度来衡量这个问题
- 为什么需要复杂度分析
- 程序测试运行结果会受到测试环境的硬件影响
- 测试结果受数据规模的影响很大
- 假设每行代码的运行时间相同,则可得到所有代码的执行时间 T(n) 与每行代码的执行次数成正比。
- 代码块:
1 int cal(int n){
2 int sum = 0; //执行 1 次
3 int i = 1: //执行 1 次
4 int j = 1; //执行 1 次
5 for(;i <= n;++i){ //执行 n 次
6 j = 1; //执行 n 次
7 for(; j <= n; ++j){ //执行 n^2 次
8 sum = sum + i * j; //执行 n^2 次
9 }
10 }
11 }
故上述代码执行时间为 $ T(n) = (2n^2+2n+3) * time $ 。
5. 大 $O$ 时间复杂度公式:
$$ T(n) = O(f(n)) $$
其中,$T(n)$ 代表代码执行时间;$n$ 表示数据规模大小;$f(n)$ 表示每行代码执行的次数总和,$O$ 表示代码的执行时间 $T(n)$ 与 $f(n)$ 表达式成正比。
大 $O$ 时间复杂度实际上并不表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,当 $n$ 很大时,公式中的低阶、常量、系数三部分并不做鱼增长趋势,所以都可以忽略。只需要记录一个最大量级就可以了。
所以上面的 $T(n)$ 的时间复杂度为 $O(n^2)$。
6. 分析代码时间复杂度的方法:
- 只关注循环执行次数最多的一段代码。
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
1 int cal(int n){
2 int ret = 0;
3 int i = 1;
4 for (; i<n; ++i){
5 ret = ret + f(i)
6 }
7 }
8
9 int f(int n){
10 int sum = 0;
11 int i = 1;
12 for(; i < n; ++i){
13 sum = sum + i;
14 }
15 return sum;
16 }
单独看 cal() 函数,假设 f(n) 只是一个普通的操作,则其 $T1(n) = O(n)$ 。但 f(n) 是一个函数,其时间复杂度是 $T2(n) = O(n)$,所以整个 cal() 函数的时间复杂度就是 ,$T(n) = T1(n)T2(n) = O(nn) = O(n^2)$
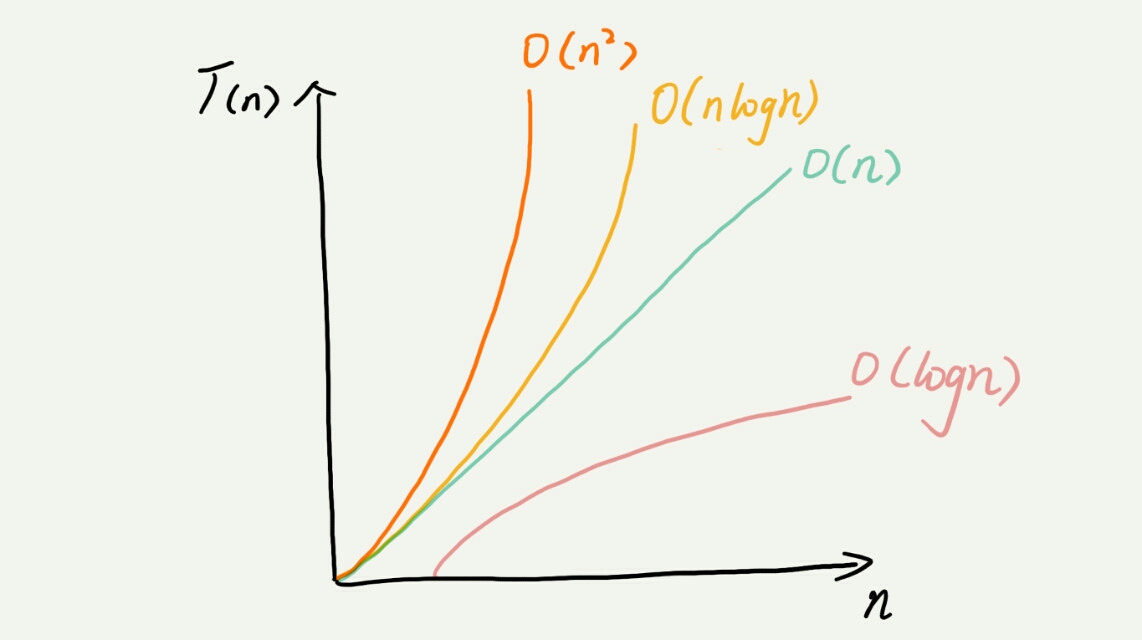
7. 常见的时间复杂度量级:

可粗路分为两类:多项式量级和非多项式量级,其中,非多项式量级只有两个:$O(2^n)$ 和 $O(n!)$。其中时间复杂度为非多项式量级的算法问题称作 NP(Non-Deterministic Ploynomial,非确定多项式)问题。
当数据规模 n 越来越大是,非多项式量级算法的执行时间会急剧增加,是非常低效的算法。
其他的量级还有 $O(m +n)$,$O(m*n)$
8. 空间复杂度:类比一下时间复杂度,表示的算法的空间与数据规模之间的增长关系。
1 void print(int n) {
2 int i = 0;
3 int[] a = new int[n];
4 for (i; i <n; ++i) {
5 a[i] = i * i;
6 }
7 for (i = n-1; i >= 0; --i) {
8 print out a[i]
9 }
10}
第 3 行申请了一个大小为 n 的 int 类型数组,剩下的代码没有占用更多的空间,所以整段代码的空间复杂度就是 $O(n)$。
常用的空间复杂度就是 $O(1)$,$O(n)$,$O(n^2)$。
参考自:极客时间《数据结构与算法之美 》专栏