1.有两个大数据 Array1和数组Array2:求两个数组的交集:
- 1).时间复杂度o(N*M) 空间复杂度o(1);
1 public static void test1(int array1[],int array2[]) 2 {// 暴力解法 3 List<Integer> E=new ArrayList<>(); 4 for(int i=0;i<array1.length;i++) 5 for(int j=0;j<array2.length;j++) 6 { 7 if(array2[j]==array1[i]) 8 E.add(array2[j]); 9 } 10 11 }
- 2). 双排序后进行比较 排序完毕后 如果array1[index1]>array2[index2] 则index2++; 否则的话index1++ ,相同的话将其放入到容器ArrayList中
算法复杂度分析 排序(桶排序算法时间复杂度 o(MlogM) )+遍历的时间= o(N*log(N)+M*log(M))+o(min(N,M)) 对其进行进一步的理解:
1 public static void test2(int array1[],int array2[]) 2 { 3 4 //1.使用快速排序 5 quick(array1,0,array1.length-1);// 使用Arrays数组中的方法 6 7 //2.使用Arrays数组中sort方法---使用快速排序 8 Arrays.sort(array2); 9 10 11 List<Integer> E=new ArrayList<>(); 12 13 int index1=0,index2=0; 14 int length=Math.min(array1.length,array2.length); 15 while(index1<length && index2<length) 16 { 17 if(array1[index1]==array2[index2]) 18 { 19 E.add(array1[index1]); 20 index1++;index2++; 21 } 22 else if(array1[index1]>array2[index2]) 23 index2++; 24 else 25 index1++; 26 } 27 28 for(int i=0;i<E.size();i++) 29 System.out.print(E.get(i)+" "); 30 }
对快速排序的方法:
1 public static void quick(int array[],int low,int hight) 2 {//叫做 挖坑填补+分治法 3 if(low<hight) 4 { 5 int middle=getMiddle(array,low,hight); 6 quick(array,low,middle-1);// 对低的表进行递归 7 quick(array,middle+1,hight);//对较高的表进行递归 8 } 9 } 10 public static int getMiddle(int array[],int start,int end) 11 {//一次遍历下来 Key小的在前方,比Key值大在后面 12 int temp=array[start]; 13 while(start<end) 14 { 15 while(start<end && array[end]>temp) 16 end--; 17 array[start]=array[end]; 18 19 while(start<end && array[start]<temp) 20 start++; 21 array[end]=array[start]; 22 23 } 24 array[start]=temp; 25 return start; 26 }
- 3)使用哈希表:将两组数据放入到哈希表中,最后只需要变量哈希集合就可以得到:空间o(N+M) 时间复杂度o(N+M)
- 当然这些解决冲突封装在hashMap,HashTable 中
在数据散列的时候 有两种方法解决冲突Hash=x mod N ; 集合中的数据随机的,不同的随机数散列到同一个地址,不得不解决位置冲突
第一种分离链接法:在产生冲突时候 使用LinkedList存取冲突的数据:一般表的大小选择 接近o(N+M)最近的素数
第二种:开放地址方法:装填因子<=0.5 超过不得不扩大表的大小2*TableSize+1,一旦发生冲突:使用线性方法,或者平方的方法大的数据表中 找新的位置来解决冲突
1 public static void test3(int array1[],int array2[]) 2 { 3 // 通过HashMap:求两个集合中交集 4 Map<Integer,Integer> map=new HashMap<>(); 5 6 for(int i=0;i<Math.min(array1.length,array2.length);i++) 7 { 8 contains(map,array1[i]); 9 contains(map,array2[i]); 10 } 11 12 // 遍历 13 for(Map.Entry<Integer, Integer>m:map.entrySet()) 14 { 15 if(m.getValue()>1) 16 System.out.println(m.getKey()); 17 } 18 } 19 20 public static void contains(Map<Integer,Integer>map,int k) 21 { 22 if(map.containsKey(k)) 23 { 24 int tmp=map.get(k); 25 tmp++; 26 map.put(k, tmp); 27 } 28 else 29 { 30 map.put(k,1); 31 } 32 }
当数据集特别大的时候可以使用MapReduce的过程的处理,Mapreduce 的原理是一个归并排序---使用数据量大但是数据种类小的
用N个Map任务和一个reduce任务,对原始数据进行分组,通过hash(item)%N将数组中的数据分到各个Map任务中
每个MAp任务求每个子集的交集处理。
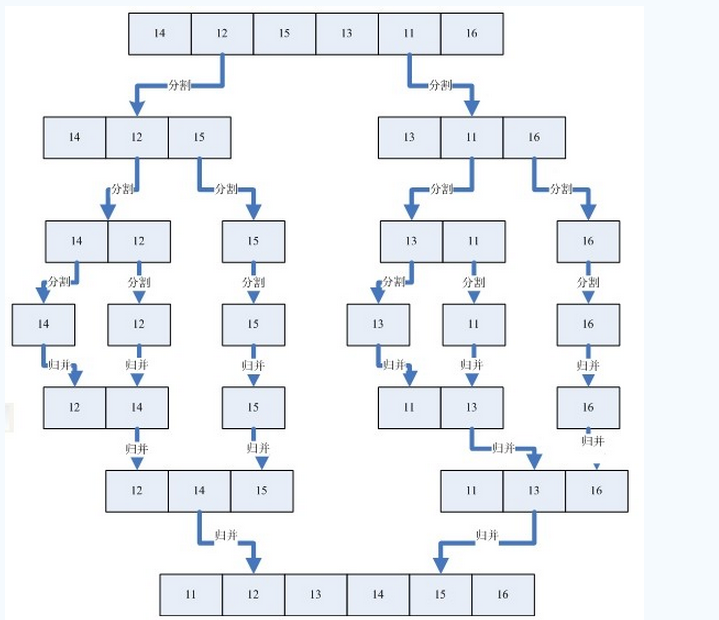
归并排序:将两个以上的有序表合并成一个新的有序表,可以用于内排序同时运用于外排序 一种稳定的排序方式,无论最好还是最坏的情况O(NlogN),辅助空间o(N)

1 public static void contains(Map<Integer,Integer>map,int k) 2 { 3 if(map.containsKey(k)) 4 { 5 int tmp=map.get(k); 6 tmp++; 7 map.put(k, tmp); 8 } 9 else 10 { 11 map.put(k,1); 12 } 13 } 14 15 public static void Merger_sort(int array[],int start,int end) 16 { 17 if(start>=end) 18 return; 19 int Mid=(start+end)/2; 20 21 Merger_sort(array,start,Mid); 22 Merger_sort(array,Mid+1,end); 23 int[]m=Merger(array,start,Mid,end); 24 25 for(int i=0;i<m.length;i++) 26 { 27 System.out.println(m[i]); 28 } 29 System.out.println(); 30 } 31 32 private static int[] Merger(int[] a, int left, int mid, int right) { 33 int r1=mid+1; 34 int tmp[]=new int[a.length]; 35 36 int tIndex = left; 37 int cIndex=left; 38 // 逐个归并 39 while(left <=mid && r1 <= right) { 40 if (a[left] <= a[r1]) 41 tmp[tIndex++] = a[left++]; 42 else 43 tmp[tIndex++] = a[r1++]; 44 } 45 // 将左边剩余的归并 46 while (left <=mid) { 47 tmp[tIndex++] = a[left++]; 48 } 49 // 将右边剩余的归并 50 while ( r1 <= right ) { 51 tmp[tIndex++] = a[r1++]; 52 } 53 54 int i=0; 55 System.out.println("第"+(++i)+"趟排序: "); 56 // TODO Auto-generated method stub 57 //从临时数组拷贝到原数组 58 while(cIndex<=right){ 59 a[cIndex]=tmp[cIndex]; 60 //输出中间归并排序结果 61 System.out.print(a[cIndex]+" "); 62 cIndex++; 63 } 64 System.out.println(); 65 return a; 66 }