数据结构-快速排序

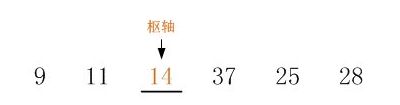
   以数列 14,11,25,37,9,28 为例,详细描述执行一趟快速排序的算法:

      1,选择待排序数列的枢轴,一般以数列的首元素作为枢轴.此数列中,我们选择首元素14作为枢轴,nPivot = 14.

      2,设定两个指针 i 和 j ,分别指向数列的首元素和尾元素. i 指向首元素14, j 指向尾元素28.示意图如下:

               

      3,向前移动尾指针 j ,使其指向从数列尾部算起首个小于枢轴(即14)的元素,并将该元素置换到头指针 i 指向的位置._nArray[i] =_nArray[j].示意图如下:

         

      首次执行该操作时 i 指针指向处的值实际上就是枢轴的值,此处的操作可以理解为 i 指针指向处的值已在之前被置换到枢轴中,此时, i 指向处已经是一个空位,在此时用找到的小于枢轴的元素填在此处.

      4,向后移动头指针 i ,使其指向从数列头部算起首个大于枢轴(即14)的元素,并将该元素置换到尾指针 j 指向的位置._nArray[j] =_nArray[i].示意图如下:

               

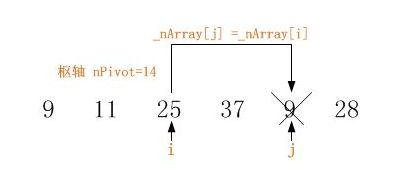
      此处同样可以理解为 j 指针指向处的值已在上一步操作中置换了出去. j 处已是一个空位.

      5,如此重复执行步骤3和步骤4,直至 i==j 时结束该循环.

      6,退出了该循环后, i 与 j 必定指向同一位置.在该位置的前部元素,其值均小于枢轴.而在该位置的后部元素,其值均大于枢轴.显而易见,此时 i 和 j 同时指向的位置就应该是枢轴的"新家"._nArray[i]=nPivot.如下图:

               

      至此,一趟排序结束.待排序数列的首元素将该数列分成了比其小和比其大的两部分.如下图:

         

      接着,我们对这一大一小两部分子数列执行相同的排序操作.

      如此"递归",直至对整个数列完成排序操作.

#include <iostream>

using namespace std;

void QuickSort(int* a,int low,int high){
    int i = low;
    int j = high;

    if(j <= i){
        return;
    }

    int tmp = a[i];

    while(i != j){
        while(a[j] > tmp && j > i){
            j--;
        }
        a[i] = a[j];
        while(a[i] < tmp && j > i){
            i++;
        }
        a[j] = a[i];
    }
    a[i] = tmp;

    QuickSort(a,low,i-1);
    QuickSort(a,i+1,high);

}

int main(){
    int a[] = {2,5,4,1,3,9,7,8,6,0};
    int n = sizeof(a)/sizeof(int);
    QuickSort(a,0,n-1);

    for(size_t i=0;i<n;i++){
        cout << a[i] << " ";
    }

    return 0;
}