
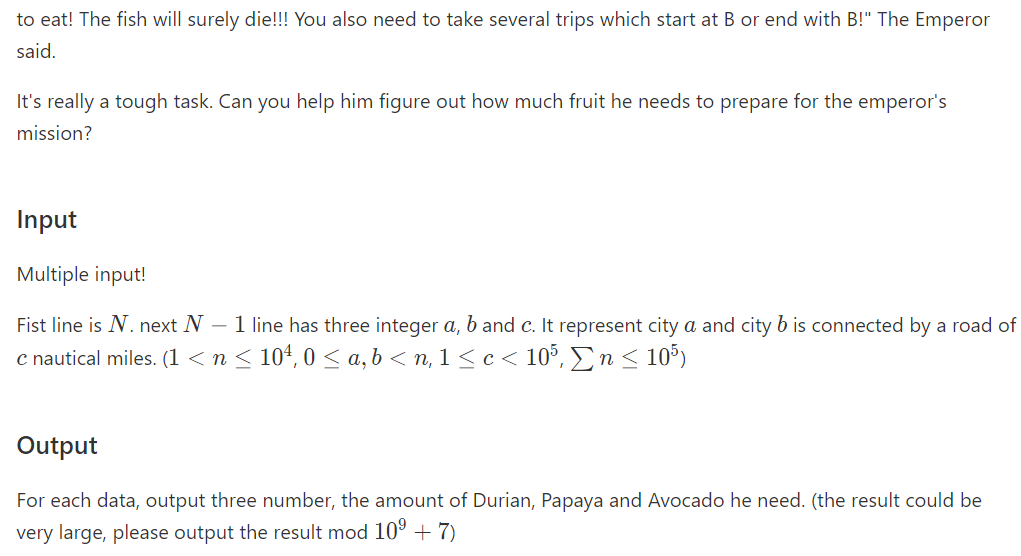
题意:求一棵树上所有路径和模3分别为0 1 2 的权值的和
思路:树形dp 增加一个记录儿子节点满足条件的个数的数组 不要放在一起dp不然答案跟新会有问题

#include <bits/stdc++.h> using namespace std; const int inf = 0x3f3f3f3f; const double eps = 1e-6; const int N = 2e4+7; typedef long long ll; const ll mod = 1e9+7 ; using namespace std; struct edge{ ll v,next,w; }; edge e[N<<1]; ll head[N]; ll tot=0; void add(ll u,ll v,ll w){ e[++tot]=edge{v,head[u],w}; head[u]=tot; } ll cnt[N][3],fcnt[N][3]; ll dp[N][3],fdp[N][3]; void dfs(ll u,ll fa){ //cout<<u<<endl; cnt[u][0]=1; for(int i=head[u];i;i=e[i].next){ ll v=e[i].v; ll w=e[i].w; if(v==fa) continue; dfs(v,u); for(int j=0;j<3;j++){ cnt[u][(j+w)%3]=(cnt[u][(j+w)%3]+cnt[v][j]); dp[u][(j+w)%3]=(dp[u][(j+w)%3]+dp[v][j]+w*cnt[v][j]%mod)%mod; //cout<<u<<" "<<dp[v][j]<<" "<<w*cnt[v][j]<<" "<<dp[u][(j+w)%3]<<endl; } } } void dfss(ll u,ll fa){ for(int i=head[u];i;i=e[i].next){ ll v=e[i].v; ll w=e[i].w; if(v==fa) continue; for(int j=0;j<3;j++){ fcnt[v][(j+w)%3]=(fcnt[u][j]+cnt[u][j]-cnt[v][((j-w)%3+3)%3]); fdp[v][(j+w)%3]=(fdp[u][j]+(dp[u][j]-dp[v][((j-w)%3+3)%3]-w*cnt[v][((j-w)%3+3)%3]%mod+mod)%mod +w*fcnt[v][(j+w)%3]%mod)%mod; } dfss(v,u); } } int main(){ ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); int n; while(cin>>n){ tot=0; memset(head,0,sizeof(head)); memset(dp,0,sizeof(dp)); memset(fdp,0,sizeof(fdp)); memset(cnt,0,sizeof(cnt)); memset(fcnt,0,sizeof(fcnt)); for(int i=1;i<n;i++){ ll u,v,w; cin>>u>>v>>w; u++; v++; add(u,v,w); add(v,u,w); } dfs(1,0); dfss(1,0); //cout<<fcnt[2][0]<<endl; ll ans[3]={0}; for(int i=1;i<=n;i++){ for(int j=0;j<3;j++){ //cout<<i<<" "<<j<<" "<<cnt[i][j]<<" "<<fcnt[i][j]<<endl; ans[j]=(ans[j]+dp[i][j]+fdp[i][j])%mod; //cout<<i<<" "<<j<<" "<<dp[i][j]<<" "<<fdp[i][j]<<endl; } } cout<<ans[0]%mod<<" "<<ans[1]%mod<<" "<<ans[2]%mod<<endl; } return 0; } /* 5 0 1 1 0 2 2 0 3 1 1 4 3 */
