P1361 小M的作物 (最小割)

题目描述

小M在MC里开辟了两块巨大的耕地A和B（你可以认为容量是无穷），现在，小P有n中作物的种子，每种作物的种子有1个（就是可以种一棵作物）（用1...n编号）。

现在，第i种作物种植在A中种植可以获得ai的收益，在B中种植可以获得bi的收益，而且，现在还有这么一种神奇的现象，就是某些作物共同种在一块耕地中可以获得额外的收益，小M找到了规则中共有m种作物组合，第i个组合中的作物共同种在A中可以获得c1i的额外收益，共同总在B中可以获得c2i的额外收益。

小M很快的算出了种植的最大收益，但是他想要考考你，你能回答他这个问题么？

输入格式

第一行包括一个整数n

第二行包括n个整数，表示ai第三行包括n个整数，表示bi第四行包括一个整数m接下来m行，

对于接下来的第i行：第一个整数ki，表示第i个作物组合中共有ki种作物，

接下来两个整数c1i，c2i，接下来ki个整数，表示该组合中的作物编号。

输出格式

只有一行，包括一个整数，表示最大收益

输入样例

3
4 2 1
2 3 2
1
2 3 2 1 2

输出样例

11

思路：我们如果不考虑那m种组合 我们可以很容易建图

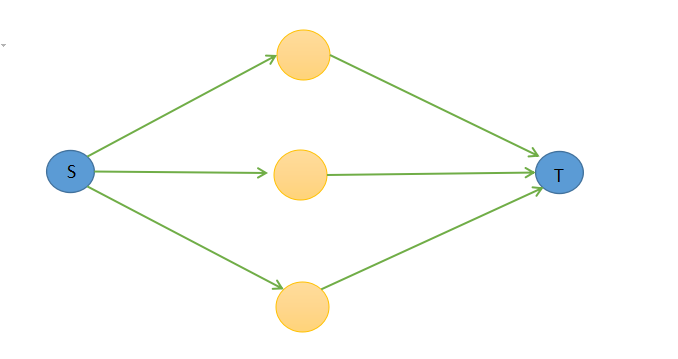
这种情况其实就是跑一边最大流 用总权值减去最小割

然后我们可以建一个虚拟节点 当作第i种组合：

这样我们还是最大流走一遍 用总权值减去最小割即可

#include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
const int maxn = 1e3+7;
const int inf = 0x3f3f3f3f;
const double eps = 1e-6;
typedef long long ll;
const ll mod = 1e7+9;
struct Edge {
  int from, to, cap, flow;
  Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};

struct Dinic {
  int n, m, s, t;
  vector<Edge> edges;
  vector<int> G[maxn];
  int d[maxn], cur[maxn];
  bool vis[maxn];

  void init(int n) {
    for (int i = 0; i < n; i++) G[i].clear();
    edges.clear();
  }

  void AddEdge(int from, int to, int cap) {
    edges.push_back(Edge(from, to, cap, 0));
    edges.push_back(Edge(to, from, 0, 0));
    m = edges.size();
    G[from].push_back(m - 2);
    G[to].push_back(m - 1);
  }

  bool BFS() {
    memset(vis, 0, sizeof(vis));
    queue<int> Q;
    Q.push(s);
    d[s] = 0;
    vis[s] = 1;
    while (!Q.empty()) {
      int x = Q.front();
      Q.pop();
      for (int i = 0; i < G[x].size(); i++) {
        Edge& e = edges[G[x][i]];
        if (!vis[e.to] && e.cap > e.flow) {
          vis[e.to] = 1;
          d[e.to] = d[x] + 1;
          Q.push(e.to);
        }
      }
    }
    return vis[t];
  }

  int DFS(int x, int a) {
    if (x == t || a == 0) return a;
    int flow = 0, f;
    for (int& i = cur[x]; i < G[x].size(); i++) {
      Edge& e = edges[G[x][i]];
      if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) {
        e.flow += f;
        edges[G[x][i] ^ 1].flow -= f;
        flow += f;
        a -= f;
        if (a == 0) break;
      }
    }
    return flow;
  }

  int Maxflow(int s, int t) {
    this->s = s;
    this->t = t;
    int flow = 0;
    while (BFS()) {
      memset(cur, 0, sizeof(cur));
      flow += DFS(s, inf);
    }
    return flow;
  }
};
int a[maxn],b[maxn];
int main(){
    Dinic x;
    int n;
    scanf("%d",&n);
    int sum=0;
    for(int i=1;i<=n;i++){
        scanf("%d",a+i);
        sum+=a[i];
    }        
    for(int i=1;i<=n;i++){
        scanf("%d",b+i);
        sum+=b[i];
    }
    int m; scanf("%d",&m);
    x.n=n+2*m+2;
    for(int i=1;i<=n;i++){
        x.AddEdge(0,i,a[i]);
        x.AddEdge(i,n+2*m+1,b[i]);
    }
    for(int i=1;i<=m;i++){
        int num; scanf("%d",&num);
        int c1,c2; scanf("%d%d",&c1,&c2);
        x.AddEdge(0,n+i,c1);
        x.AddEdge(n+m+i,n+2*m+1,c2);
        sum+=c1+c2;
        for(int j=1;j<=num;j++){
            int v; scanf("%d",&v);
            x.AddEdge(n+i,v,inf);
            x.AddEdge(v,n+m+i,inf);
        }
    }
    printf("%d
",sum-x.Maxflow(0,n+2*m+1));
}