poj 1661 Help Jimmy (dp)

Description

"Help Jimmy" 是在下图所示的场景上完成的游戏。 

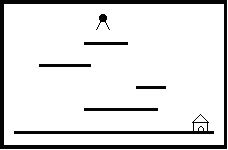
场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。 

Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。 

设计一个程序，计算Jimmy到底地面时可能的最早时间。 

Input

第一行是测试数据的组数t（0 <= t <= 20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i = 1..N）。所有坐标的单位都是米。 

Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。 

Output

对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。

Sample Input

1

3 8 17 20

0 10 8

0 10 13

4 14 3

Sample Output

23

 

思路:先按照高度从高到低排序 然后就从上往下dp dp[i][0/1] 表示第i条边从(0)左边或者(1)右边的最优走法，bug很多很多 思路虽然早就想到了 但是搞了两个晚上 一直在poj上用数据测试(poj上讨论里面的数据) 最后终于过了！

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<bitset>
#include<cstdlib>
#include<cmath>
#include<set>
#include<list>
#include<deque>
#include<map>
#include<queue>
#define ll long long int
using namespace std;
inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
int moth[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int dir[4][2]={1,0 ,0,1 ,-1,0 ,0,-1};
int dirs[8][2]={1,0 ,0,1 ,-1,0 ,0,-1, -1,-1 ,-1,1 ,1,-1 ,1,1};
const int inf=0x3f3f3f3f;
const ll mod=1e9+7;
struct node{
    int l,r,h;
};
node p[100007];
int dp[100007][2];
bool cmp(node a,node b){
    return a.h>b.h;
}
int main(){
    ios::sync_with_stdio(false);
    int t;
    cin>>t;
    while(t--){
        memset(dp,inf,sizeof(dp));
        int n,x,y,maxn;
        cin>>n>>x>>y>>maxn;
        for(int i=1;i<=n;i++)
            cin>>p[i].l>>p[i].r>>p[i].h;
        p[n+1].h=0;
        p[n+1].l=-20001;
        p[n+1].r=20001;
//        p[0].l=p[0].r=x;
//        p[0].h=y;
        sort(p+1,p+2+n,cmp);
    //    dp[0][0]=dp[0][1]=0;
    //    cout<<dp[pos][0]<<" "<<dp[pos][1]<<endl;
        int pos=-1;
        for(int i=1;i<=n+1;i++){
            if(p[i].l<=x&&x<=p[i].r){
                pos=i;
                break;
            }
        }
        if(pos==n+1)
        dp[pos][0]=dp[pos][1]=0;
        else{
            dp[pos][0]=abs(x-p[pos].l);
            dp[pos][1]=abs(p[pos].r-x);
        }
        for(int i=pos+1;i<=n+1;i++){
            //int temp=inf;
            int po;
            for(int j=pos;j<i;j++){
                if(p[j].h-p[i].h>maxn) continue;
                bool f1=1; bool f2=1;
                for(int k=j+1;k<i;k++){
                    if(p[k].l<=p[j].l&&p[k].r>=p[j].l)
                        f1=0;
                    if(p[k].r>=p[j].r&&p[k].l<=p[j].r)
                        f2=0;
                }
                if(i==n+1){
                    if(f1&&p[j].l>=p[i].l&&p[j].l<=p[i].r){
                        dp[i][0]=min(dp[i][0],dp[j][0]);
                        dp[i][1]=min(dp[i][1],dp[j][0]);
                    }
                    if(f2&&p[j].r>=p[i].l&&p[j].r<=p[i].r){
                        dp[i][0]=min(dp[i][0],dp[j][1]);
                        dp[i][1]=min(dp[i][1],dp[j][1]);
                    }
                }else{
                    if(f1&&p[j].l>=p[i].l&&p[j].l<=p[i].r){
                        dp[i][0]=min(dp[i][0],dp[j][0]+abs(p[j].l-p[i].l));
                        dp[i][1]=min(dp[i][1],dp[j][0]+abs(p[j].l-p[i].r));
                    }    
                    if(f2&&p[j].r>=p[i].l&&p[j].r<=p[i].r){
                        dp[i][0]=min(dp[i][0],dp[j][1]+abs(p[j].r-p[i].l));
                        dp[i][1]=min(dp[i][1],dp[j][1]+abs(p[j].r-p[i].r));
                    }    
                }
            //    cout<<j<<" "<<f1<<" "<<f2<<" "<<p[j].l<<" "<<p[j].r<<" "<<p[i].l<<" "<<p[i].r<<endl;    
            }
            
            //cout<<i<<" "<<dp[i][0]<<" "<<dp[i][1]<<endl;
        }
        cout<<min(dp[n+1][0],dp[n+1][1])+y<<endl;
    }
    return 0;
}