问题模型 - 已经两个序列求解二叉树遍历的其他序列
问题描述: 此类问题通常会告诉我们两种序列,其中一种一定包含中序序列。
我们需要根据这两种序列求出另外的序列。
此类问题根据需求又可以分以下两种情况
-
根据两种序列求层序序列 / 要求你进行建立完整的二叉树结构
-
根据两种序列求前序 / 后序序列
对于以上类问题来说,第一种问题要求我们必须进行建立一棵完整的二叉树结构,而第二种则不需要建立完整的树形结构,只需要进行遍历即可。
现假设我们有一个树其结构如图所示。
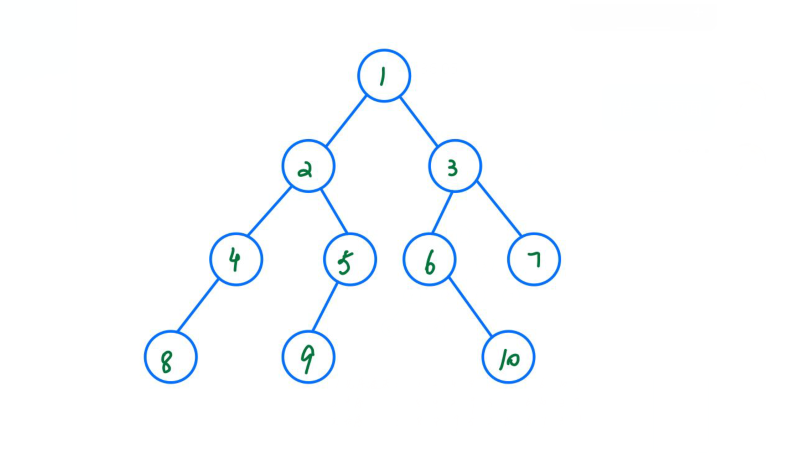
根据树的结构我们可以知道
先序遍历序列为 : 1 2 4 8 5 9 3 6 10 7
中序遍历序列为 : 8 4 2 9 5 1 6 10 3 7
后序遍历序列为 : 8 4 9 5 2 10 6 7 3 1
在这个给定的树形结构的前提下我们来尝试讨论如何解决以上提出的问题。
类型一 : 已知先序序列和中序序列
首先我们已知了先序序列和中序序列,接下来我们只需要遵循一个原则来划分这个树的左右子树即可。
我们知道先序遍历的第一个元素一定是整棵树的根节点 , 其次我们可以到中序遍历中找到这个根节点所在位置,这个位置的左边的所有元素是以当前点为根的左子树,这个位置的右边的所有元素是以当前结点为根的右子树
如图所示:
既然我们已经确定了第一个根节点为先序序列的第一个结点,那么我们首先可以得到整棵树的根节点和该节点的左右子树都有哪些元素但是此时并不知道左右子树的结构
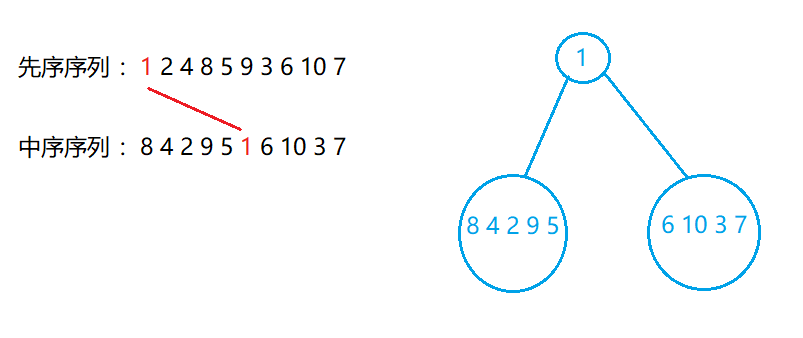
然后根据此规则我们递归的去还原左右子树的结构:
首先是左子树:
此时既然我们既然是子树,我们就不能再用之前的完整的序列进行划分子树,我们需要对之前的序列进行拆分,拆分出来左子树的部分
如何进行拆分呢?
1.记录下来此时根节点左边的元素个数,此时根节点 1 左边有 5 个元素 那么在先序序列中从 1 开始选取长度为 5 的一段序列作为左子树的先序序列 : 2 4 8 5 9
2.由于中序序列的两边就是树形结构的左子树和右子树,所以我们只需要将根节点 1 左边的部分照搬下来即可。此时的中序序列为: 8 4 2 9 5 1
然后根据这两组序列我们可以在根据之前所定义好的规则进行新的左右子树的划分。

其次来拆分右子树:
1.记录下来此时根节点左边的元素个数,此时根节点 1 左边有 5 个元素 那么在先序序列中从 1 开始选取长度为 n - root + 5 的一段序列作为左子树的先序序列 : 3 6 7 10
2.由于中序序列的两边就是树形结构的左子树和右子树,所以我们只需要将根节点 1 右边的部分照搬下来即可。此时的中序序列为: 6 10 3 7
然后根据这两组序列我们可以在根据之前所定义好的规则进行新的左右子树的划分。

根据以上规则我们最终可以恢复整颗二叉树结构。
下面我们考虑如何用代码实现以上的思想
我们定义一组变量x , y 来圈定当前子树的先序序列的范围 , 另一组变量 p , q 来圈定当前子树的中序序列的范围
那么每一次 我们的 x 变量所记录的位置一定是这个子树的根,利用变量 k 来记录当前根结点 x 在中序序列中的位置
那么此时
左子树的划分一定是: [x + 1 , x + k - p] , [p , k - 1]
右子树的划分一定是: [x + k - p + 1, y] , [k + 1 ,q]
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
int in[N], pre[N], n;
int find(int x)
{
for(int i = 0; i < n; i ++)
if(in[i] == x)return i;
return -1;
}
void getpost(int x, int y, int p, int q)
{
if(x > y || p > q)return;
int k = find(pre[x]);
getpost(x + 1, x + k - p, p, k - 1);
getpost(x + k - p + 1, y, k + 1, q);
cout << pre[x] << " ";
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)cin >> pre[i];
for(int i = 0; i < n; i ++)cin >> in[i];
getpost(0, n - 1, 0, n - 1);
return 0;
}
类型二 : 已知后序序列和中序序列
原理和以上方法类似,但是需要明确的是后序遍历的最后一个结点为根
后序遍历的左右子树划分(具体i , q 请结合代码注意分析与上一种略有不同)
左子树的划分一定是: [x , y - k - 1] , [p , i - 1]
右子树的划分一定是: [y - k, y - 1] , [i + 1 ,q]
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
int in[N], pre[N], post[N], n;
int find(int x)
{
for(int i = 0; i < n; i ++)
if(in[i] == x) return i;
return -1;
}
void getpre(int x, int y, int p, int q)
{
if(x > y || p > q) return;
int i = find(post[y]), k = q - i;
cout << post[y] << " ";
getpre(x, y - k - 1, p, i - 1);
getpre(y - k, y - 1, i + 1, q);
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)cin >> post[i];
for(int i = 0; i < n; i ++)cin >> in[i];
getpre(0, n - 1, 0, n - 1);
return 0;
}