题目链接:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
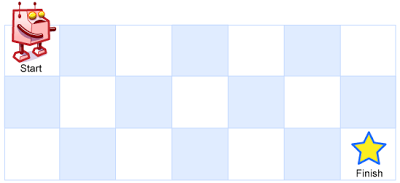
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
-
1 <= m, n <= 100 -
题目数据保证答案小于等于
2 * 109
解题思路
-
确定dp数组以及其下标的含义
该题的dp数组是一个二维数组。
dp[i,j]表示从(0,0)出发到(i,j)的路径数 -
确定递推公式
题目中表示每一步只能向下或向右移动,所以要走到
(i,j)处,只能从从(i,j-1)处向下走一步或从(i-1,j)处向右走一步。所以可以得到递推公式:dp[i,j] = dp[i,j - 1] + dp[i - 1,j] -
dp数组的初始化
从
(0, 0)到(i, 0)的路径只有一条,所以dp[i,0] = 1,同理,dp[0,j] = 1 -
确定遍历顺序
由递推公式可以看出
dp[i,j]是由其上方和其左方推到出来的,所以遍历顺序是从左到右一层一层地遍历的 -
举例推导dp数组
当
m=3,n=7时,dp数组如下所示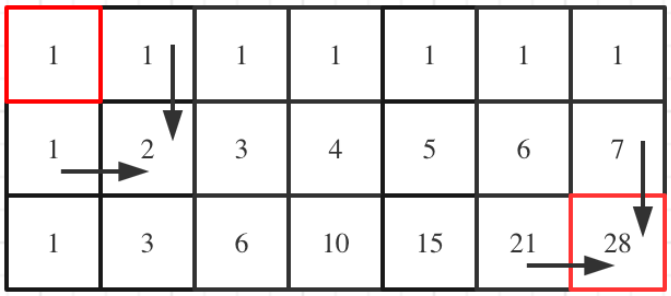
C++
class Solution { public: int uniquePaths(int m, int n) { int dp[m][n]; //M行N列,用i表示行,j表示列 for (int i = 0; i < m; i++) dp[i][0] = 1; for (int j = 0; j < n; j++) dp[0][j] = 1; for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } return dp[m - 1][n - 1]; } };
JavaScript
/** * @param {number} m * @param {number} n * @return {number} */ var uniquePaths = function(m, n) { //JS中创建二维数组的方法...... const dp = new Array(m); for (let i = 0; i < m; i++) { dp[i] = new Array(n); } for (let i = 0; i < m; i++) dp[i][0] = 1; for (let j = 0; j < n; j++) dp[0][j] = 1; for (let i = 1; i < m; i++) { for (let j = 1; j < n; j++) { dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } return dp[m - 1][n - 1]; };
时间复杂度:O(m × n)