题目链接:
题目描述
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
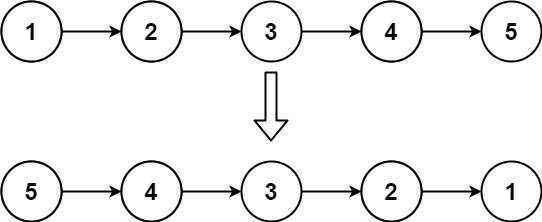
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
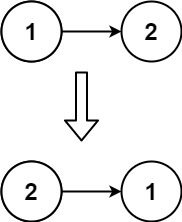
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
-
链表中节点的数目范围是 [0, 5000]
-
-5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
题解
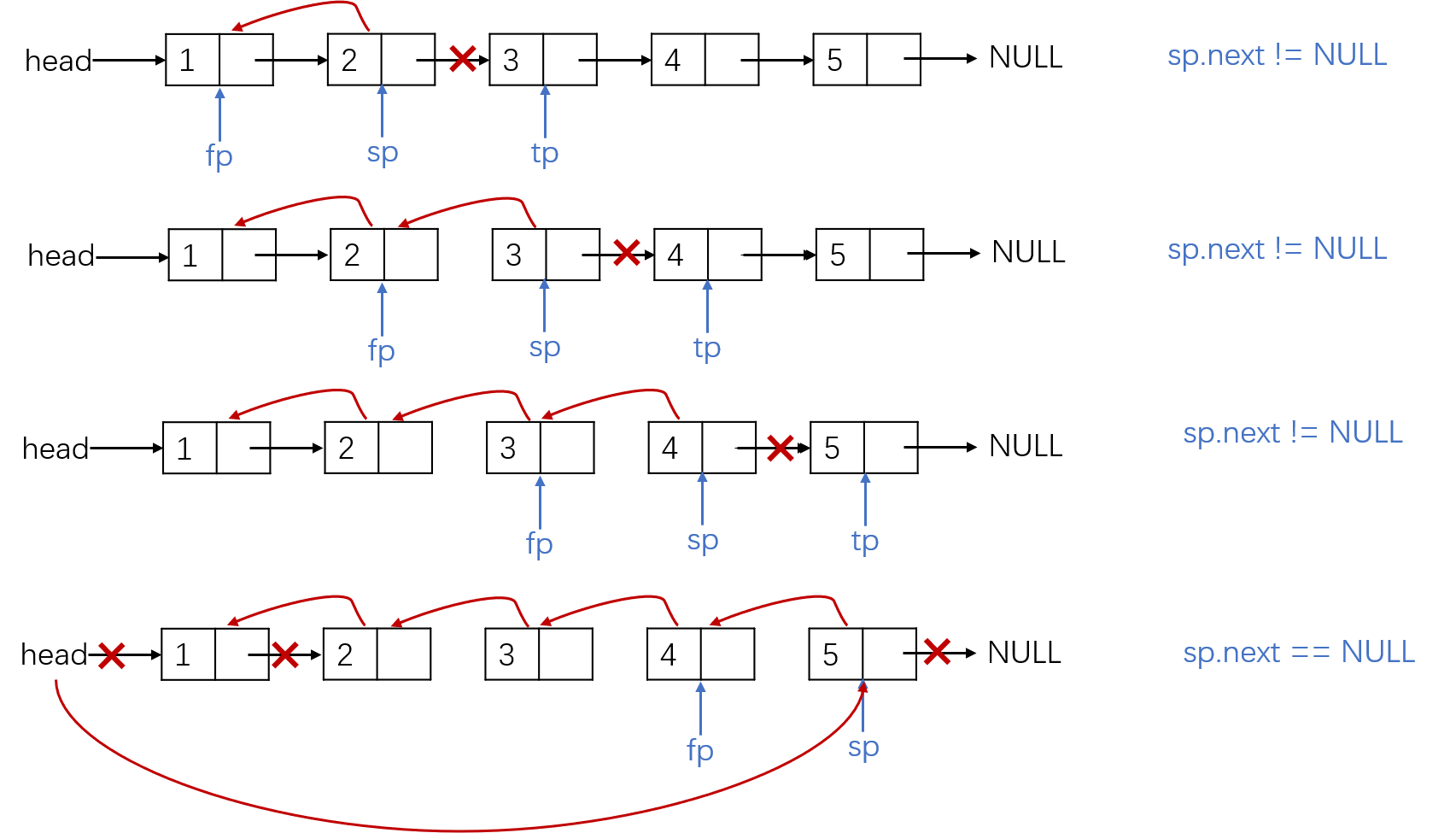
思路:如下图,利用三个指针
代码(C++版本)
ListNode* reverseList(ListNode* head) { //链表中只有没有节点和只有一个节点的情况 if (head == NULL || head->next ==NULL) { return head; }
ListNode* tp; ListNode* fp = head; ListNode* sp = fp->next; while (sp->next != NULL) { tp = sp->next; sp->next = fp; fp = sp; sp = tp; } sp->next = fp; head->next = NULL; head = sp; return head; }
分析:
-
时间复杂度:O(N)
-
空间复杂度:O(1)
官方题解
链接:
方法一:迭代 假设链表为 1→2→3→∅,我们想要把它改成 ∅←1←2←3。
在遍历链表时,将当前节点的next 指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
class Solution { public: ListNode* reverseList(ListNode* head) { ListNode* prev = nullptr; ListNode* curr = head; while (curr) { ListNode* next = curr->next; curr->next = prev; prev = curr; curr = next; } return prev; } };
复杂度分析
-
时间复杂度:O(n),其中 n 是链表的长度。需要遍历链表一次。
-
空间复杂度:O(1)。
方法二:递归 递归版本稍微复杂一些,其关键在于反向工作。假设链表的其余部分已经被反转,现在应该如何反转它前面的部分?

class Solution { public: ListNode* reverseList(ListNode* head) { if (!head || !head->next) { return head; } ListNode* newHead = reverseList(head->next); head->next->next = head; head->next = nullptr; return newHead; } };
复杂度分析
-
时间复杂度:O(n),其中 n 是链表的长度。需要对链表的每个节点进行反转操作。
-
空间复杂度:O(n),其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间,最多为 n 层。
代码随想录
思路
如果再定义一个新的链表,实现链表元素的反转,其实这是对内存空间的浪费。
其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:
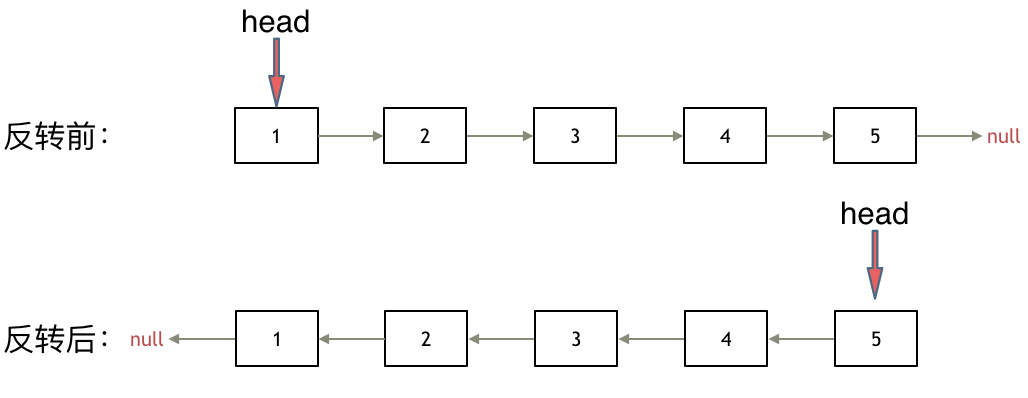
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改表next指针的方向。
双指针法
那么接下来看一看是如何反转呢?
我们拿有示例中的链表来举例,如动画所示:
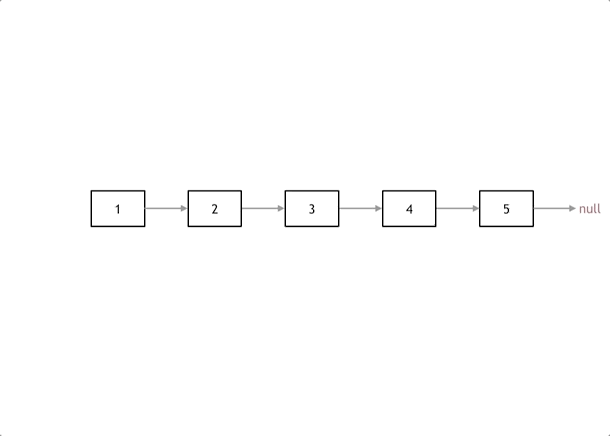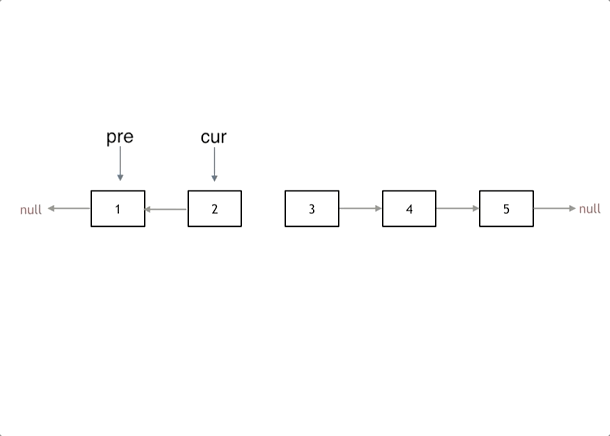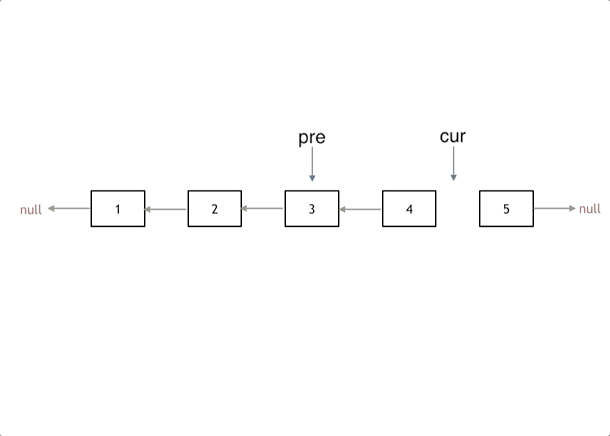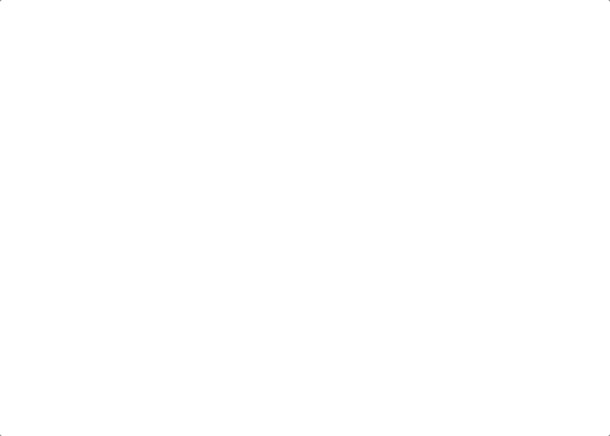
首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
然后就要开始反转了,首先要把 cur->next 节点用tmp指针保存一下,也就是保存一下这个节点。
为什么要保存一下这个节点呢,因为接下来要改变 cur->next 的指向了,将cur->next 指向pre ,此时已经反转了第一个节点了。
接下来,就是循环走如下代码逻辑了,继续移动pre和cur指针。
最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时我们return pre指针就可以了,pre指针就指向了新的头结点。
代码(C++)
class Solution { public: ListNode* reverseList(ListNode* head) { ListNode* temp; // 保存cur的下一个节点 ListNode* cur = head; ListNode* pre = NULL; while(cur) { temp = cur->next; // 保存一下 cur的下一个节点,因为接下来要改变cur->next cur->next = pre; // 翻转操作 // 更新pre 和 cur指针 pre = cur; cur = temp; } return pre; } };
递归法
递归法相对抽象一些,但是其实和双指针法是一样的逻辑,同样是当cur为空的时候循环结束,不断将cur指向pre的过程。
关键是初始化的地方,可能有的同学会不理解, 可以看到双指针法中初始化 cur = head,pre = NULL,在递归法中可以从如下代码看出初始化的逻辑也是一样的,只不过写法变了。
具体可以看代码(已经详细注释),
class Solution { public: ListNode* reverse(ListNode* pre,ListNode* cur){ if(cur == NULL) return pre; ListNode* temp = cur->next; cur->next = pre; // 可以和双指针法的代码进行对比,如下递归的写法,其实就是做了这两步 // pre = cur; // cur = temp; return reverse(cur,temp); } ListNode* reverseList(ListNode* head) { // 和双指针法初始化是一样的逻辑 // ListNode* cur = head; // ListNode* pre = NULL; return reverse(NULL, head); } };