统计知识选讲（二）——主成分分析（PCA）的推导和应用

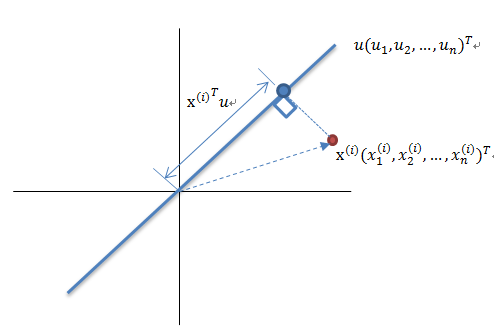
1、数学推导

根据上讲的思想，我们可以用下图来进行数学上的推导.

 

2、PCA的步骤

1）对原始数据进行标准化处理：对该指标变量进行标准化，

2）计算相关系数矩阵（协方差矩阵）

3）计算相关系数矩阵的特征值和特征向量，得到新的指标标量。

4）计算特征值的信息贡献率和累积贡献率，按一定规则选择主成分

5）以主成分的贡献率为权重，构建主成分综合评价模型，计算综合评价值和排名

3、应用实例——我国各地区普通高等教育发展综合评价

案例背景不再详述，在此我们选取10个指标来评价30个省市他们的普通高等教育发展。

数据：

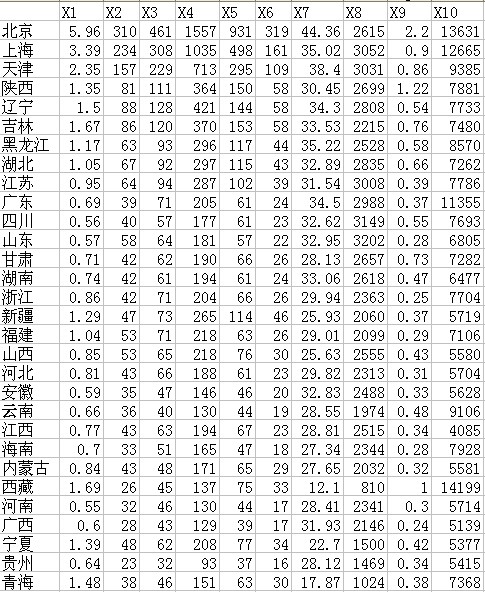
1）将上述数据标准化，计算协方差矩阵

2）计算协方差矩阵的特征值和特征值贡献率

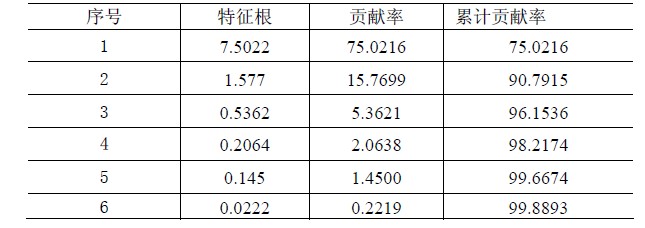
3）根据特征值贡献率选取前四个特征根对应的特征向量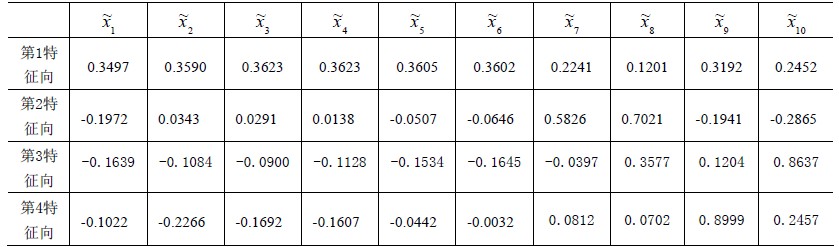

由此可得四个主成分分别为：

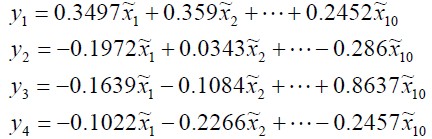
4）分别以四个主成分的贡献率为权重，计算主成分综合得分：

 

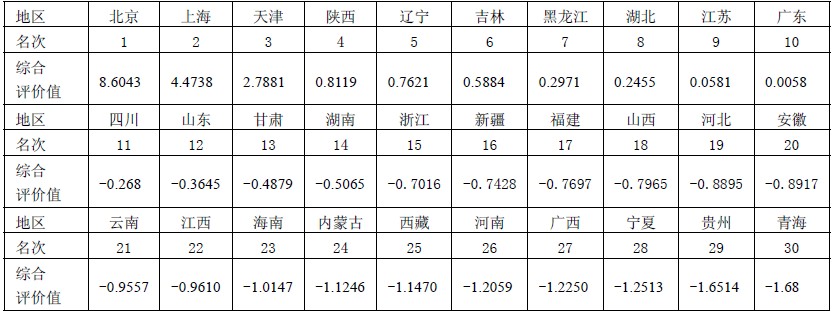
计算的matlab程序：

gj=[
5.96    310    461    1557    931    319    44.36    2615    2.2        13631;
3.39    234    308    1035    498    161    35.02    3052    0.9        12665;
2.35    157    229    713        295    109    38.4    3031    0.86    9385;
1.35    81    111    364        50    58    30.45    2699    1.22    7881;
1.5        88    128    421        144    58    34.3    2808    0.54    7733;
1.67    86    120    370        153    58    33.53    2215    0.76    7480;
1.17    63    93    296        117    44    35.22    2528    0.58    8570;
1.05    67    92    297        115    43    32.89    2835    0.66    7262;
0.95    64    94    287        102    39    31.54    3008    0.39    7786;
0.69    39    71    205        61    24    34.5    2988    0.37    11355;
0.56    40    57    177        61    23    32.62    3149    0.55    7693;
0.57    58    64    181        57    22    32.95    3202    0.28    6805;
0.71    42    62    190        66    26    28.13    2657    0.73    7282;
0.74    42    61    194        61    24    33.06    2618    0.47    6477;
0.86    42    71    204        66    26    29.94    2363    0.25    7704;
1.29    47    73    265        114    46    25.93    2060    0.37    5719;
1.04    53    71    218        63    26    29.01    2099    0.29    7106;
0.85    53    65    218        76    30    25.63    2555    0.43    5580;
0.81    43    66    188        61    23    29.82    2313    0.31    5704;
0.59    35    47    146        46    20    32.83    2488    0.33    5628;
0.66    36    40    130        44    19    28.55    1974    0.48    9106;
0.77    43    63    194        67    23    28.81    2515    0.34    4085;
0.7        33    51    165        47    18    27.34    2344    0.28    7928;
0.84    43    48    171        65    29    27.65    2032    0.32    5581;
1.69    26    45    137        75    33    12.1    810           1    14199;
0.55    32    46    130        44    17    28.41    2341    0.3        5714;
0.6        28    43    129        39    17    31.93    2146    0.24    5139;
1.39    48    62    208        77    34    22.7    1500    0.42    5377;
0.64    23    32    93        37    16    28.12    1469    0.34    5415;
1.48    38    46    151        63    30    17.87    1024    0.38    7368;
];%原始数据
gj=zscore(gj);                   %数据标准化
r=corrcoef(gj);                  %计算相关系数矩阵
[e,lamda]=eig(r);                %求相关系数矩阵的特征值和特征向量
lamda=sort(sum(lamda),'descend');%将特征值降序排列
attribute=lamda./sum(lamda);     %各特征值的贡献率
cum_attribute=cumsum(attribute); %累计的贡献率
num=4;                           %选取的主成分的个数
df=gj*e(:,10:-1:11-num)          %新指标下的样本值
score=attribute(1:num)*df';      %计算综合得分
[stf,ind]=sort(score,'descend'); %把得分按照从高到低的次序排列
stf=stf', ind=ind'