词嵌入技术解析（二）

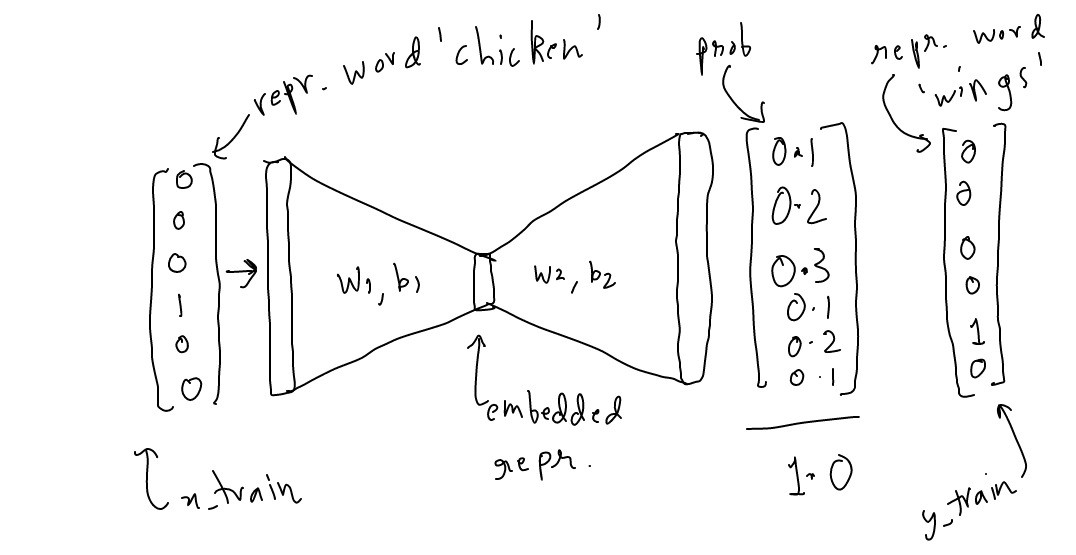
在文章词嵌入的那些事儿（一）中，我们得到了以下结论：

1. 词嵌入是一种把词从高维稀疏向量映射到了相对低维的实数向量上的表达方式。
2. Skip-Gram和CBOW的作用是构造神经网络的训练数据。
3. 目前设计的网络结构实际上是由DNN+softmax()组成。
4. 计算词嵌入向量实际上就是在计算隐藏层的权矩阵。
5. 对于单位矩阵的每一维(行)与实矩阵相乘，可以简化为查找元素1的位置索引从而快速完成计算。

本文主要是在上文的基础上，对模型的隐藏层-输出层的设计做进一步探索。

1. 霍夫曼编码

霍夫曼编码（Huffman Coding），又译为哈夫曼编码、赫夫曼编码，是一种用于无损数据压缩的熵编码（权编码）算法。

霍夫曼树常处理符号编写工作。根据整组数据中符号出现的频率高低，决定如何给符号编码。如果符号出现的频率越高，则给符号的码越短，相反符号的号码越长。假设我们要给一个英文单字"F O R G E T"进行霍夫曼编码，而每个英文字母出现的频率分别如下图所示。

1.1 创建霍夫曼树

进行霍夫曼编码前，我们先创建一个霍夫曼树，具体步骤如下：

1. 将每个英文字母依照出现频率由小排到大，最小在左，如上图所示。
2. 每个字母都代表一个终端节点（叶节点），比较F.O.R.G.E.T六个字母中每个字母的出现频率，将最小的两个字母频率相加合成一个新的节点。如Fig.2所示，发现F与O的频率最小，故相加2+3=5。
3. 比较5.R.G.E.T，发现R与G的频率最小，故相加4+4=8。
4. 比较5.8.E.T，发现5与E的频率最小，故相加5+5=10。
5. 比较8.10.T，发现8与T的频率最小，故相加8+7=15。
6. 最后剩10.15，没有可以比较的对象，相加10+15=25。
7. 最后产生的树状图就是霍夫曼树，参考下图。 

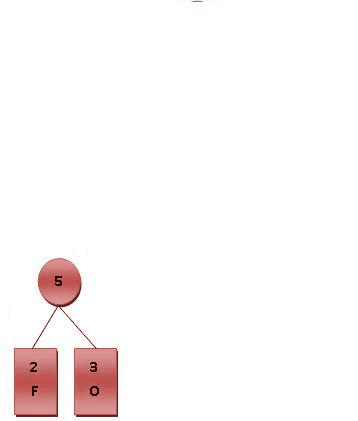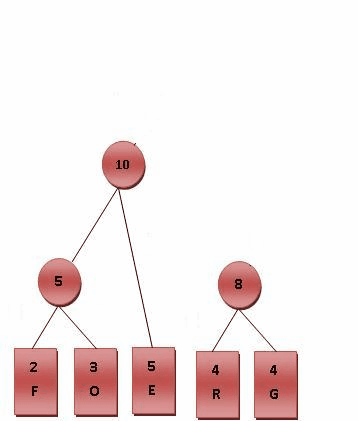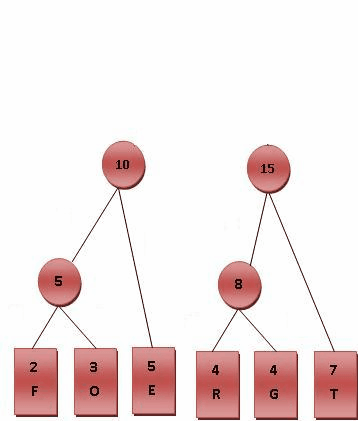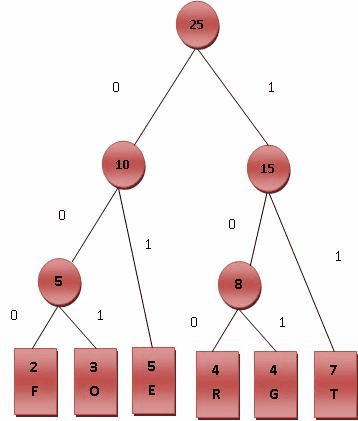
1.2 进行编码

给霍夫曼树的所有左节点设置为'0'，所有右节点设置为'1'。

从根节点到叶子节点依序记录所有字母的编码，如下图所示：

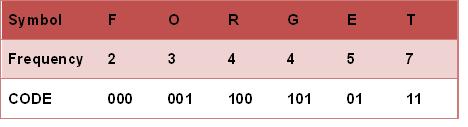
以上步骤就是对词进行霍夫曼编码的操作步骤。可以看到，词的出现频率越高，越靠近根节点，且编码长度越短。

2. Hierarchical Softmax的理解

首先回顾一下softmax函数。softmax(规范化指数函数)是网络输出层的函数，用于计算包含至少两种不同类型的词嵌入向量。此外，它也经常被用作为神经网络的激活函数，类似的还包括sigmoid和tanh等函数。softmax的公式如下：

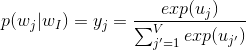
其中，激活输出向量的每个元素都是在给定输入单词I的情况下，等于词汇表中第j个单词时的概率。同时，激活输出向量的所有元素之和等于1且每个元素映射到区间[0,1]。这个算法的计算复杂度即是词汇表的大小O(V)。实践表明，我们可以通过使用二叉树结构来有效地地减少此计算复杂度。下面，将介绍Hierarchical Softmax。

使用Hierarchical Softmax的主要原因是其计算复杂度是以2为底V的对数。

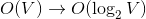
每个单词都可以通过从根节点-内部节点的路径到达，此外，对这个路径的度量可以由沿着这条路径的各概率乘积表示。各个概率值由sigmoid函数产生：

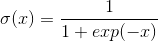
其中x由输入和输出向量的点积求出，n(w,j)表示为从根节点到叶子结点w（即上下文单词）的路径上的第j个节点。

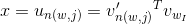
实际上，我们可以用概率p来代替sigmoid函数。对于每个内部节点，我们都选择了一个任意子节点(左或右)，并将正的sigmoid函数值赋给其中的一个(通常是左子节点)。

通过保留这些约束，节点n的左子节点的sigmoid函数可以描述为:

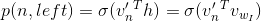
同理，节点n的右子节点的sigmoid函数可以描述为:

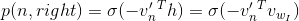
所以，输出词的计算概率为:

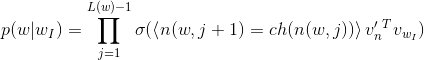
其中，L(w)表示霍夫曼树的深度，ch(n)表示节点n的子节点；角大括号表示布尔检验是否为真或假：如果布尔检验为True，说明节点n与其子节点ch(n)都在树的左边，即其子节点为左子节点。反之，如果布尔值为False，即其子节点ch(n)为右子节点。

回顾词嵌入的那些事儿（一）基于Tensorfow的Skip-Gram极简实现的内容，模型输出的其实是预测目标词的概率，也就是说每一次预测都要基于全部的数据集进行softmax()概率计算。神经网络结构如下图所示：

而采用Hierarchical Softmax后，由于替换了之前的softmax()函数，所以，隐藏层的词嵌入向量不需要对词汇表每个单词计算其为输出词的概率。

例如假设输出词是w2，因此可以沿着霍夫曼树从根节点（即词嵌入向量）一直走到我们的叶子节点w2（输出词）。由下图可以观察到，仅需执行3步的sigmoid函数计算，就可以确定叶子节点w2的位置。这无疑大大减少了操作数。

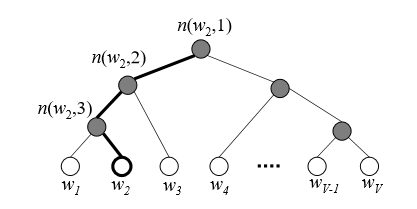
实际上，我们在计算词嵌入向量所采用的霍夫曼编码与第一节的介绍基本一致，区别只是对左右节点的0 1计数有所不同，比如：

3. Negative Sampling的理解

那么，霍夫曼树是不是计算词嵌入向量的最优解？假设我们的训练样本里的中心词w是一个很生僻的词，那么就得在霍夫曼树中一直往下寻找路径。能不能不用搞这么复杂的一颗霍夫曼树，将模型变的更加简单呢？Negative Sampling就是这么一种求解word2vec模型的方法，它摒弃了霍夫曼树，采用了Negative Sampling（负采样）的方法来求解，下面我们就来看看Negative Sampling的求解思路。

首先，需要了解噪声对比估计(NCE)。

3.1 噪声对比估计(NCE)

噪声对比估计(NCE)的核心思想是通过logistic回归将一个多分类问题转化为一个二分类问题，同时保留学习到的词向量的质量。在NCE中，词向量不再是通过从中心词中预测上下文单词来学习，相反通过学习如何从（target, random word from vocabulary）对中区分出真实的（target, context）对从而完成词向量的计算。换句话说，如果一个模型能够从随机噪声中分辨出实际的目标词对和上下文词对，那么好的词向量就会被学习。

3.2 Negative Sampling

而Negative Sampling是基于噪声对比估计(类似于生成对抗性网络)的一种方法。

即一个好的模型应该通过逻辑回归来区分假信号和真实信号。同时Negative Sampling背后的思想类似于随机梯度下降：不是每次都改变所有的权重，考虑到我们所拥有的成千上万的观测数据，我们只使用了其中的K个，并且显著地提高了计算效率：

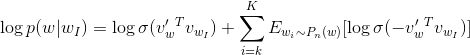
正如上图公式，与随机梯度下降法的区别在于，我们不仅考虑了一个观测结果还考虑了其中的K个。

对于训练数据集，我们使用的是具有噪声分布的数据集。之所以使用这种噪声分布数据集，是为了区分真实数据和我们试图解决的假数据。具体来说，对于每个正样本(即 true target/context pair)，我们从噪声分布中随机抽取k个负样本，并feed进模型。对于小的训练数据集，建议k值在5到20之间，而对于非常大的数据集，k值在2到5之间就足够了。我们的模型只有一个输出节点，它可以预测这对数据是随机噪声数据还是真实有效的target/context对。

由于采用了随机采样，所以需要假定一个概率分布。在词汇表中每个单词wi被采样到的概率由下式决定，其中幂为3/4。之所取3/4是因为可以减弱由于不同频次差异过大造成的单词采样差异的影响，使得小频次的单词也有一定被采样的概率。f(w)是词汇表中单词w出现的频率：

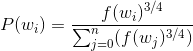
举例说明：

在采样前，我们将长度为1的线段划分成M等份，这里M>>V，这样可以保证每个词对应的线段都会划分成对应的区间块。在采样时，我们只需要从M个区间中采样出neg个区间，此时采样到的每一个区间块对应到的线段所属的词就是我们的负例词。 

可能会有疑问：使用Negative Sampling后，负样本数量较多，正样本只有一个，会不会出现样本不均衡的现象从而导致逻辑回归模型分错左右子节点？实际上，样本不均衡这种问题主要出现在分类算法中。而我们这里词向量的训练本质不是一个分类问题，所以问题不大。

最后，一般来讲，NCE是一种渐近无偏的一般参数估计技术，而Negative Sampling更经常被用在二分类模型（例如逻辑回归）中，它们对词向量学习有用，但不是作为通用估计器去执行其他机器学习任务。具体可以参考这篇论文：Notes on Noise Contrastive Estimation and Negative Sampling 。

4. 总结

1. 霍夫曼编码会使得出现频率最高的词编码长度最短，且路径最短。
2. Negative Sampling的核心思想是每次训练只随机取一小部分的负例使他们的概率最小，以及对应的正例概率最大。
3. 相比于Hierarchical Softmax，Negative Sampling不再采用霍夫曼树，而是采用随机负采样。
4. 从计算效率上讲，Negative Sampling优于Hierarchical Softmax优于Softmax。

5. 参考资料

[1] 维基百科：霍夫曼编码

[2] Language Models, Word2Vec, and Efficient Softmax Approximations

[3] word2vec(cbow skip-gram hierarchical softmax Negative sampling)模型深度解析