回转游戏（IDA* DFS 剪枝）

如下图所示，有一个“#”形的棋盘，上面有1,2,3三种数字各8个。

给定8种操作，分别为图中的A~H。

这些操作会按照图中字母和箭头所指明的方向，把一条长为8的序列循环移动1个单位。

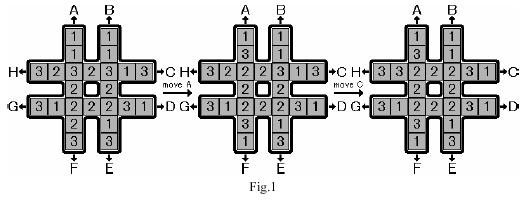
例如下图最左边的“#”形棋盘执行操作A后，会变为下图中间的“#”形棋盘，再执行操作C后会变成下图最右边的“#”形棋盘。

给定一个初始状态，请使用最少的操作次数，使“#”形棋盘最中间的8个格子里的数字相同。

输入格式
输入包含多组测试用例。

每个测试用例占一行，包含24个数字，表示将初始棋盘中的每一个位置的数字，按整体从上到下，同行从左到右的顺序依次列出。

输入样例中的第一个测试用例，对应上图最左边棋盘的初始状态。

当输入只包含一个“0”的行时，表示输入终止。

输出格式
每个测试用例输出占两行。

第一行包含所有移动步骤，每步移动用大写字母“A~G”中的一个表示，字母之间没有空格，如果不需要移动则输出“No moves needed”。

第二行包含一个整数，表示移动完成后，中间8个格子里的数字。

如果有多种方案，则输出字典序最小的解决方案。

输入样例：
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0
输出样例：
AC
2
DDHH
2

这里使用迭代加深来进行优化 不规定层数 直接遍历 看看到那一层能够结束就行 不需要一直往下面遍历
两个剪枝 ： 一个是每一个操作的对立操作 直接跳过
第二个使用估价函数

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 24;
int center[8] = {6,7,8,11,12,15,16,17};
int op[8][7] =
{
    {0,2,6,11,15,20,22},
    {1,3,8,12,17,21,23},
    {10,9,8,7,6,5,4},
    {19,18,17,16,15,14,13},
    {23,21,17,12,8,3,1},
    {22,20,15,11,6,2,0},
    {13,14,15,16,17,18,19},
    {4,5,6,7,8,9,10}
};
int oppsite[8] = {5,4,7,6,1,0,3,2};
int q[N];
int path[120];

int f()
{
   static int sum[4];
    memset(sum, 0, sizeof sum);
  
        for(int j = 0; j < 8 ; j++)
        {
          sum[q[center[j]]]++;
        }
    
    int s = 0;
    for(int i = 1; i < 4 ; i ++) s= max(s,sum[i]);
    return 8 - s;
}

void operate(int x)
{
    int t = q[op[x][0]];
    for(int i = 0 ; i < 6 ; i++) q[op[x][i]] = q[op[x][i+1]];
    q[op[x][6]] = t;
}


bool dfs(int u , int depath,int last)
{
    if(u + f() > depath) return false;
    
    if(!f()) return true;
    
    for(int i = 0 ; i < 8 ; i ++)
    {
        if(oppsite[i] != last)
        {
           operate(i);//进行i个操作
           path[u] = i;
           if(dfs(u+1,depath,i))return true;
           operate(oppsite[i]);//恢复现场
            
        }
    }
    
    
    return false;
}

int main()
{
   while(cin >> q[0] , q[0])//先输入第0位 然后从第一位开始输出
   {
       for(int i = 1 ; i < 24 ; i ++) 
       {
           cin >> q[i];
       }
       
       int  depath = 0 ;
       while(!dfs(0,depath,-1))depath++;//当前层数 总共层数 上一次操作
       
       if(!depath) printf("No moves needed");//第一次就不需要排序 直接返回
       else {
           for(int i = 0 ; i < depath ; i ++) printf("%c", 'A' + path[i]);
        
       }
         printf("
%d
", q[6]);
       
   }
   return 0 ;
}