---边缘检测概念理解---
边缘检测的理解可以结合前面的内核,说到内核在图像中的应用还真是多,到现在为止学的对图像的操作都是核的操作,下面还有更神奇的!
想把边缘检测出来,从图像像素的角度去想,那就是像素值差别很大,比如X1=20和X2=200,这两个像素差值180,在图像的显示就非常明显,这样图像的边缘不就体现出来了?但是问题来了,一幅图像给你,如果一个像素一个像素对比,
1.周围像素差别不大的怎么办?
2.周围相差很大,但是很多的怎么办?
3.怎么样才能更好地区别图像的边缘呢?
比如5-200比较肯定算一个边缘,但是200-200比较久不是边缘了。如果全部做对比的话有很多的问题存在,这只是一个简单的问题。

---范谈各种边缘检测---
从上面的分析可以得到,边缘检测->>>>>就是分离那些相差大的像素
如何分离像素,现在脑子里有个映像:利用核去处理图像!
A. Robert算子检测边缘:

x和y方向的算子
观察上诉的算子,可以发现和我们刚开始设想的一个一个比较差不多,比如本来比如X1=20和X2=40,这两个像素差值20,但是20体现不出来,所以用1,-1来增大这种差值,这其实解决了我们上诉遇到的第一点问题了,但是后面的两点依然没有解决。
具体的例子我们可以用opencv自带的API,addwight进行试验,把核改一下就行了。。。
Roberts算子检测方法对具有陡峭的低噪声的图像处理效果较好,但是利用roberts算子提取边缘的结果是边缘比较粗,因此边缘的定位不是很准确。
B. Sobel算子检测边缘:
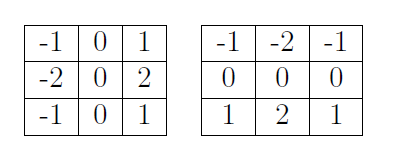
X和Y方向

对XY两个方向的梯度进行合并
Sobel算子如果光从核上面去看,根本什么都不知道,我们得去看他的原理->>>>
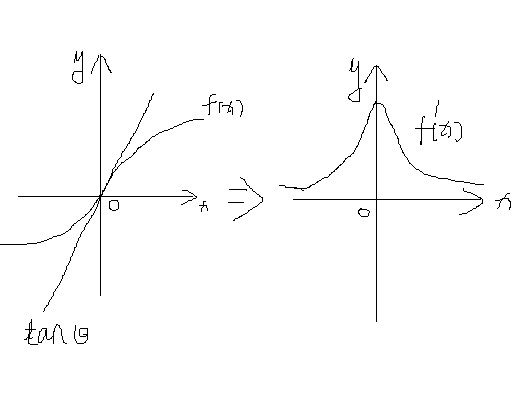
他的原理就是利用导数求解边缘,我们知道像素差别大的时候那么它的切点越陡峭,那么这个时候就找到了边缘!具体程序怎么实现的,我还没弄懂,感觉是利用拉普拉斯变化之后再计算的,最后用一个算子近似代替。。。(个人YY)
Sobel算子检测方法对灰度渐变和噪声较多的图像处理效果较好,sobel算子对边缘定位不是很准确,图像的边缘不止一个像素。
C. Laplacian算子检测边缘:
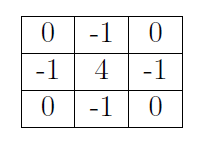
拉普拉斯算子
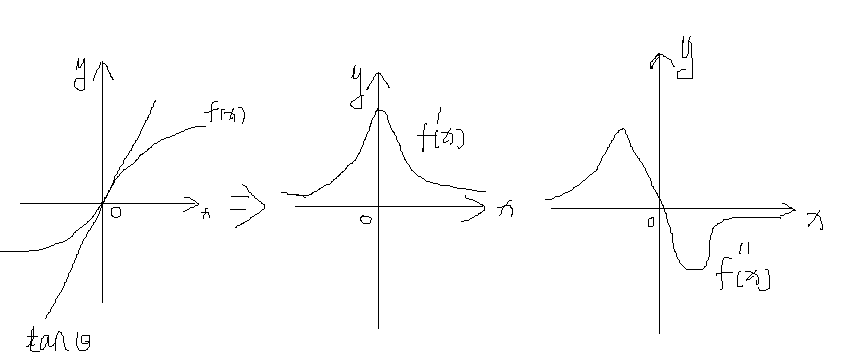
拉普拉斯边缘检测是通过二阶倒数,从上面的一阶倒数的理解就不难发现二阶倒数是怎么进行的了。
二阶倒数比一阶倒数的好处是在与受到周围的干扰小,其不具有方向性,操作容易,且对于很多方向的图像处理好。
Laplacian算子法对噪声比较敏感,所以很少用该算子检测边缘,而是用来判断边缘像素视为与图像的明区还是暗区。
C. Scharr算子检测边缘:
这个滤波是Sobel的升级版,原理是一样的,就是实现的近似代替不一样,说白了就事核改进了。。。
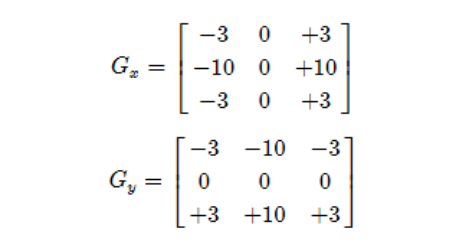
D. Canny算子检测边缘:
这是比较新的算法,运用的也是最广泛的。这个算法是在Sobel算法的基础上改进的,和Scharr不一样!
Canny的步骤是:1.给一张图片,先进行滤波消除干扰,滤波前面博客已经说明。
2.计算梯度(进行Sobel算子计算)。
3.非极大值抑制。
4.滞后阈值。
下面一届具体介绍->>>>
在opencv2.0的时候,直接调用API就帮你完成全部的工作,包含上面的四部。
现在opencv3.0滤波得自己操作,API完成了后三步操作。
这里在Sobel运行之后的基础上对图像的边缘进行了优化,哪些是优秀的,哪些是差的,在这里会处理。
---细谈边缘检测---
上面讲到Canny的非极大值抑制和滞后阈值,其中这两点是这个算法的核心!
非极大值抑制:
从字面上的理解就是从一群数据中找到真正的极大值,对于不是极大值的省略或者抑制显示。
我们来想一下,Sobel算子计算的值就是边缘的值吗?1.算子是固定的,那就有很大的几率会计算到不是边缘的数据。
2.计算的结果不会省略不好的点,也不会去加强好的点,所以显示就不明显。
我们的目的就是改进上面两个点,对于第一个点,我们得比较那些计算的点进行比较,把不好点舍去--->>>
以前在神经网络那篇博文里提到过“梯度”的概念,就是数据下降或者上升最快的方向,简单的说就是求导切线的方向!
试想一下我们在这个方向上找最大和最小值是最快最准确的,这个具体原因神经网络那篇博文说过了,可以去看看。

通过计算我们得到了θ的值在[-π/2,+π/2]区间,然后我们就可以比较在这个方向上的G和左右G1、G2的大小,当G>G1、G2的时候,那就说明这个G就是局部极大值,从而保留下来:

例如:G0的θ是45度,那么在它的梯度方向来对比它是不是最大值,如果是的话那就说明它是局部极大值->判断G0和(G3、G6)的大小关系!G0 = G0>G3&&G0>G6? G0:0;
上面的方法是第一代非极大值抑制算法,缺点是当 θ!=0、45、90、180 时,那么旁边的八个值就不在θ的梯度上,就没办法去做比较了,这时候出现第二代算法--->>>
插值法运用在非最大值抑制算法中:

插值法:就是y=kx+b的插值公式,比如:X1和X2中间想插一点X,X = X1 + k(X2-X1)或者X= k*X1 +(1-k)X2 当然插值法还有其它形式,不过两点的线性插值比较简单的。这里使用第二者!
上面的图形是当 |Gy|>|Gx| && Gx*Gy>0 的情况。前者保障靠近y轴,后者保证θ>0.
注释:在有的文章上看的和我说的相反,按照数学知识应该是这样的啊,具体原因我也不知道了。
令 k = |Gy/Gx|
G23 = k*G2 + (1-k)*G3;
G67 = k*G6 + (1-k)*G7;
G0 = G0>G23 && G0>G67 ? G0:0;或者这里可以突出重点给定G0的值G0 = G0>G23 && G0>G67 ? 200:0;
opencv的源码就是使用这种方法的,大家可以参考源码:
1 void NonMaxSuppress(int*pMag,int* pGradX,int*pGradY,SIZE sz,LPBYTE pNSRst) 2 { 3 LONG x,y; 4 int nPos; 5 // the component of the gradient 6 int gx,gy; 7 // the temp varialbe 8 int g1,g2,g3,g4; 9 double weight; 10 double dTemp,dTemp1,dTemp2; 11 //设置图像边缘为不可能的分界点 12 for(x=0;x<sz.cx;x++) 13 { 14 pNSRst[x] = 0; 15 pNSRst[(sz.cy-1)*sz.cx+x] = 0; 16 17 } 18 for(y=0;y<sz.cy;y++) 19 { 20 pNSRst[y*sz.cx] = 0; 21 pNSRst[y*sz.cx + sz.cx-1] = 0; 22 } 23 24 for (y=1;y<sz.cy-1;y++) 25 { 26 for (x=1;x<sz.cx-1;x++) 27 { 28 nPos=y*sz.cx+x; 29 // if pMag[nPos]==0, then nPos is not the edge point 30 if (pMag[nPos]==0) 31 { 32 pNSRst[nPos]=0; 33 } 34 else 35 { 36 // the gradient of current point 37 dTemp=pMag[nPos]; 38 // x,y 方向导数 39 gx=pGradX[nPos]; 40 gy=pGradY[nPos]; 41 //如果方向导数y分量比x分量大,说明导数方向趋向于y分量 42 if (abs(gy)>abs(gx)) 43 { 44 // calculate the factor of interplation 45 weight=fabs(gx)/fabs(gy); 46 g2 = pMag[nPos-sz.cx]; // 上一行 47 g4 = pMag[nPos+sz.cx]; // 下一行 48 //如果x,y两个方向导数的符号相同 49 //C 为当前像素,与g1-g3 的位置关系为: 50 //g1 g2 51 // C 52 // g4 g3 53 if(gx*gy>0) 54 { 55 g1 = pMag[nPos-sz.cx-1]; 56 g3 = pMag[nPos+sz.cx+1]; 57 } 58 //如果x,y两个方向的方向导数方向相反 59 //C是当前像素,与g1-g3的关系为: 60 // g2 g1 61 // C 62 // g3 g4 63 else 64 { 65 g1 = pMag[nPos-sz.cx+1]; 66 g3 = pMag[nPos+sz.cx-1]; 67 } 68 } 69 else 70 { 71 //插值比例 72 weight = fabs(gy)/fabs(gx); 73 g2 = pMag[nPos+1]; //后一列 74 g4 = pMag[nPos-1]; // 前一列 75 //如果x,y两个方向的方向导数符号相同 76 //当前像素C与 g1-g4的关系为 77 // g3 78 // g4 C g2 79 // g1 80 if(gx * gy > 0) 81 { 82 g1 = pMag[nPos+sz.cx+1]; 83 g3 = pMag[nPos-sz.cx-1]; 84 } 85 86 //如果x,y两个方向导数的方向相反 87 // C与g1-g4的关系为 88 // g1 89 // g4 C g2 90 // g3 91 else 92 { 93 g1 = pMag[nPos-sz.cx+1]; 94 g3 = pMag[nPos+sz.cx-1]; 95 } 96 } 97 //--线性插值等价于dTemp1 = g1 + weight*(g2-g1)--// 98 dTemp1 = weight*g1 + (1-weight)*g2; 99 dTemp2 = weight*g3 + (1-weight)*g4; 100 //当前像素的梯度是局部的最大值 101 //该点可能是边界点 102 if(dTemp>=dTemp1 && dTemp>=dTemp2) 103 { 104 pNSRst[nPos] = 128; 105 } 106 else 107 { 108 //不可能是边界点 109 pNSRst[nPos] = 0; 110 } 111 } 112 } 113 } 114 }
在论文中海油一个改进的插值,用二次插值代替一次插值,学过数值分析的都知道,一次插值在直线很好,但是在曲线不好,当然二次插值也不能消除很多误差,当然海油牛顿插值等等。。。
这是当Gx和Gy同号的情况,另一种情况自己想一下就行了。


二次插值相比较一次插值的优点是:不用考虑哪个哪个具体的角度。其实很多人都提到了0、45、90、180的角度划分,我这里没有提到,原理是一样的,我感觉直接做就好了,没必要再去弄个中间变量过度一下,可能为了理解吧。
滞后阈值:
1. T1, T2为阈值,凡是高于T2的都保留,凡是小于T1都丢弃。
2.如果介于T1和T2之间的话,判断是否连接T2,如果没连接T2那就删除。
3.T1和T2比例最好1:2/1:3
这里说明一下第二点:
A.我们的目的是找到最大边缘变化。
B.并且保证边缘显示效果很好。
对于A来说,我们非最大值抑制已经找到部分最大值,现在用T2再进行一遍,已经很好的达到我们A目的了。
对于B来说,用T1去滤去可能不是最大值的点,现在用第二点来加强显示,在T2附近的保留,不在的都删除(意思就是在最小值附近)。
看下面这个例子,T1=2,T2=9 用核3X3去找T2附近的值,那就表示只有6个值可以保留,其他值都将被删除。
第一步:整个图像去找T>T2和T<T1的值,删除或者保留,并且标记记录。
第二步:在上一步记录的最大值附近寻找存在的值,直接删除或者保留。

参考:《自适应Canny算法研究及其在图像边缘检测中的应用_金刚》
http://blog.csdn.net/kezunhai/article/details/11620357