灰度预测+LinearSVR和ARIMA预测财政收入

 

数据

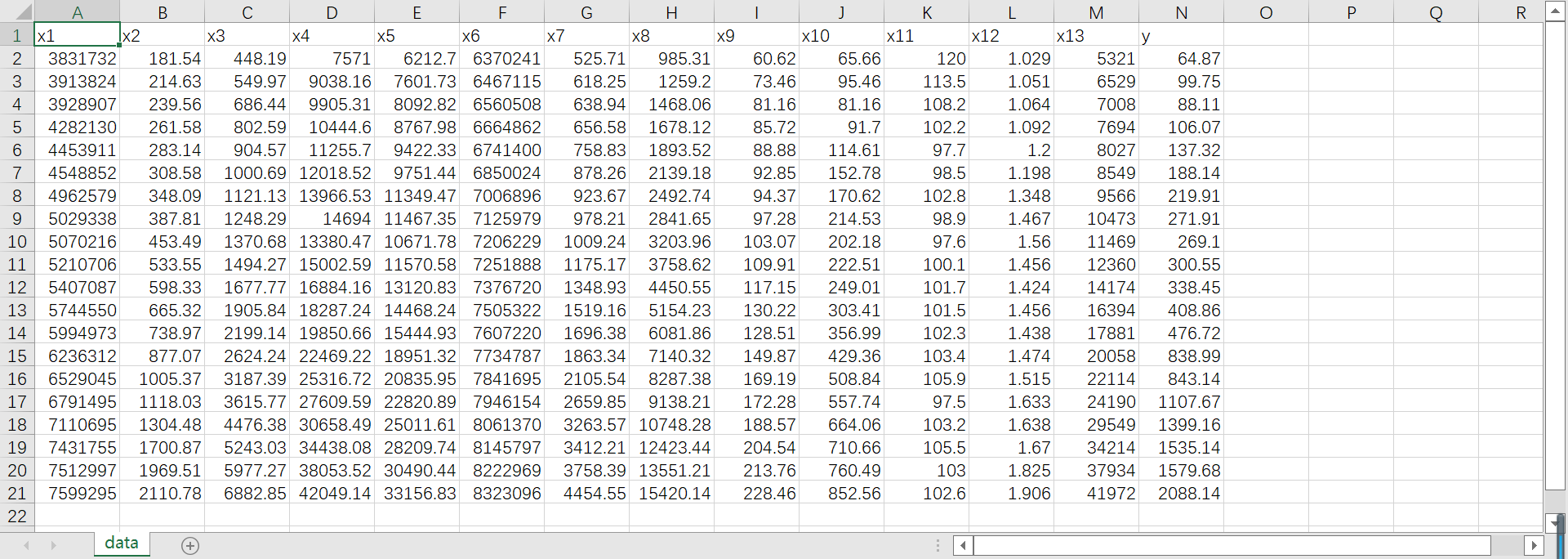
一、灰度预测+LinearSVR

灰度预测

import pandas as pd
import numpy as np
from sklearn.linear_model import Lasso

inputfile = 'E:/PY1/data/data.csv' # 输入的数据文件
data = pd.read_csv(inputfile) # 读取数据

lasso = Lasso(1000) # 调用Lasso()函数，设置λ的值为1000
lasso.fit(data.iloc[:,0:13],data['y'])

data = data.iloc[:, 0:13]

mask = lasso.coef_ != 0 # 返回一个相关系数是否为零的布尔数组
outputfile ='./tmp/new_reg_data.csv' # 输出的数据文件
new_reg_data = data.iloc[:, mask] # 返回相关系数非零的数据
new_reg_data.to_csv(outputfile) # 存储数据
print('输出数据的维度为：',new_reg_data.shape) # 查看输出数据的维度

LinearSVR

import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR

inputfile = 'E:/PY1/data/new_reg_data_GM11.xls' # 灰色预测后保存的路径
data = pd.read_excel(inputfile) # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13'] # 属性所在列
data_train = data.iloc[0:20].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std # 数据标准化
x_train = data_train[feature].values # 属性数据
y_train = data_train['y'].values # 标签数据

linearsvr = LinearSVR() # 调用LinearSVR()函数
linearsvr.fit(x_train,y_train)
x = ((data[feature] - data_mean[feature])/data_std[feature]).values # 预测，并还原结果。
data['y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
outputfile = 'E:/PY1/new_reg_data_GM11_revenue.xls' # SVR预测后保存的结果
data.to_excel(outputfile)

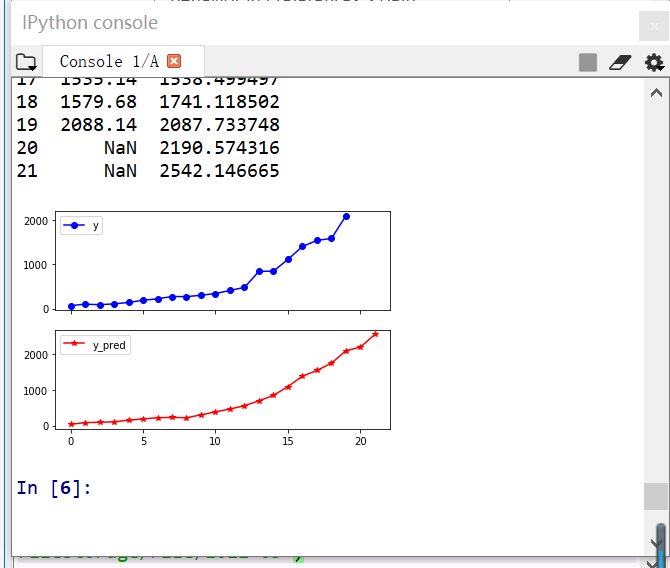
print('真实值与预测值分别为：\n',data[['y','y_pred']])

fig = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*']) # 画出预测结果图
plt.show()

结果

 

二、AERIMA

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号

inputfile = 'E:PY1/data/data.csv' # 输入的数据文件
data = pd.read_csv(inputfile) # 读取数据

datetime = range(1994, 2014)
# X = list(datetime)
X = []
for i in datetime:
X.append(str(i))

y = data['y']

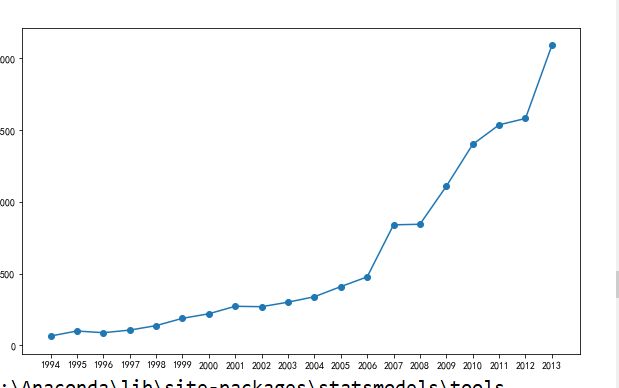
# 时序图
plt.figure(figsize=(10, 6))
plt.plot(X, y)
plt.scatter(X, y)
plt.show()
pre_data = pd.DataFrame()
pre_data['X'] = X
pre_data['y'] = y
pre_data.set_index('X', inplace=True)
pre_data.head()
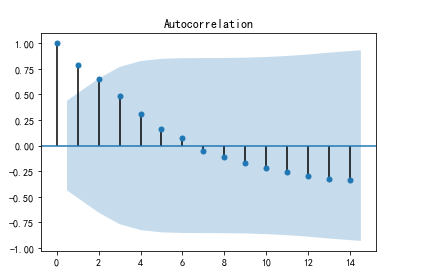
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(pre_data).show()
# 平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print('原始序列的ADF检验结果为：', ADF(pre_data['y']))
# 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
import warnings
warnings.filterwarnings("ignore")

# 差分后的结果
D_data = pre_data.diff().dropna()
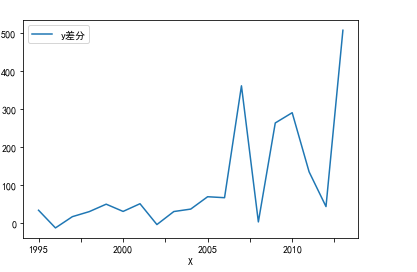
D_data.columns = ['y差分']
D_data.plot() # 时序图
plt.show()
plot_acf(D_data).show() # 自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show() # 偏自相关图
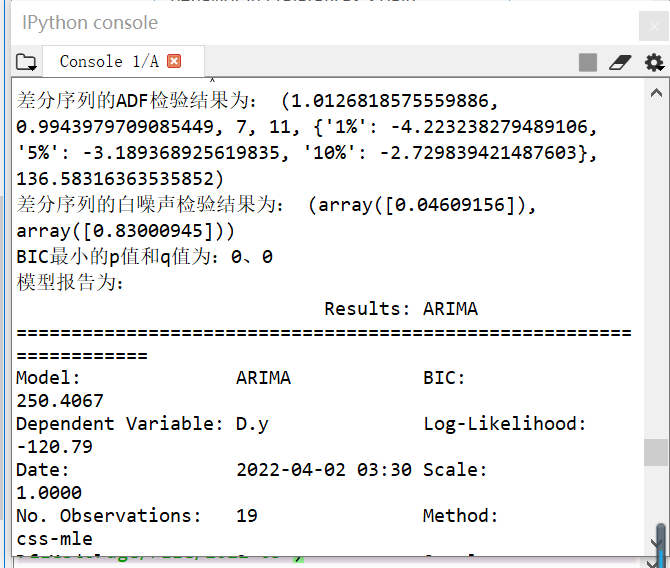
print('差分序列的ADF检验结果为：', ADF(D_data['y差分'])) # 平稳性检测
from statsmodels.stats.diagnostic import acorr_ljungbox
print('差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) # 返回统计量和p值
from statsmodels.tsa.arima_model import ARIMA

# 定阶
pre_data['y'] = pre_data['y'].astype(float)
pmax = int(len(D_data)/10) # 一般阶数不超过length/10
qmax = int(len(D_data)/10) # 一般阶数不超过length/10
bic_matrix = [] # BIC矩阵
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try: # 存在部分报错，所以用try来跳过报错。
tmp.append(ARIMA(pre_data, (p,1,q)).fit().bic)
except:
tmp.append(None)
bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix) # 从中可以找出最小值

p,q = bic_matrix.stack().astype('float64').idxmin() # 先用stack展平，然后用idxmin找出最小值位置。
print('BIC最小的p值和q值为：%s、%s' %(p,q))

model = ARIMA(pre_data, (0,1,1)).fit()
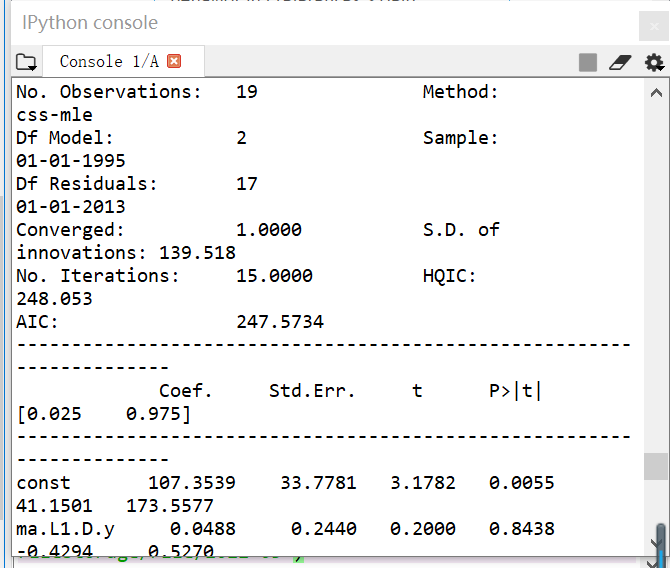
print('模型报告为：\n', model.summary2())
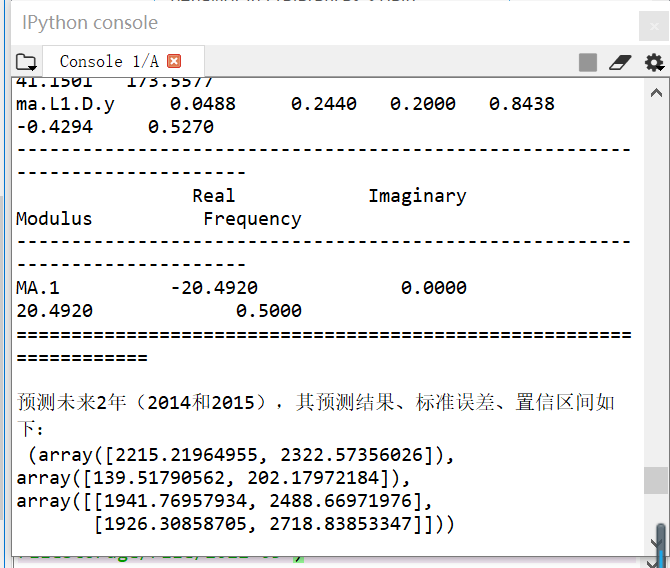
print('预测未来2年（2014和2015），其预测结果、标准误差、置信区间如下：\n', model.forecast(2))

结果

 

 

 

 

 

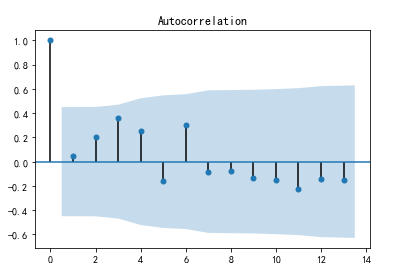
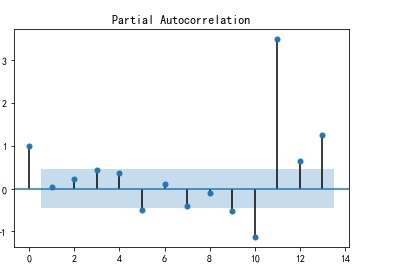
三、结论

灰度预测+LinearSVR算法预测的模型更好