转载于https://www.luogu.org/blog/sincereactor/shu-shang-ci-fen-di-liang-zhong-sai-lu
例题
先摆一波题
运输计划;
疫情控制;
一.关于边的差分(如找被所有路径共同覆盖的边)
首先我们除了一般的grand,depth等数组以外,多开两个数组:tmp和prev。
tmp用来记录点的出现次数(具体点说实际上记录的是点到其父亲的边的出现次数),prev记录每个点到其父亲的那条边。对于一条起点s,终点t的路径。我们这样处理:
tmp[s]++,tmp[t]++,tmp[LCA(s,t)]-=2。(记住:最后要从所有叶结点把权值向上累加。)以一次操作为例,我们来看看效果(可以画一张图)。首先tmp[s]++,一直推上去到根,这时候s到root的路径访问次数都+1,tmp[t]++后,t到lca路径加了1,s到lca路径加了1,而lca到根的路径加了2。
这时,我们只需要tmp[LCA(s,t)]-=2,推到根,就能把那些多余的路径减掉,达到想要的目的。而这是一次操作,对于很多次操作的话,我们只需要维护tmp,而不必每次更新到根,维护好tmp最后Dfs一遍即可。这时如果tmp[i]==次数的话,说明i到其父亲的边是被所有路径覆盖的。如图

二.关于点的差分(如将路径上的所有点权值加一,求最后点的权值)
此操作中我们这样维护:每次经过一条边,(如从u到v)我们让tmp[u]++,tmp[v]++,tmp[LCA(u,v)]--,tmp[grand[LCA(u,v)][0]]--。(最后要把tmp推上去)
以一次添加为例想象一下,首先u到根的路径上tmp都+1,此时u到根间结点tmp都为1,之后v到根路径上tmp+1,此时u到LCA前一个,v到LCA前一个点的tmp都+1,而LCA到根的所有点都+2,然后从tmp[LCA]--,更新上去,此时u-v路上所有tmp都+1,已经达到目的。
而多余的是什么部分呢,也就是LCA的上一个结点(grand[LCA][0])到根的这一段都多加了1,所以tmp[grand[LCA][0]]--,更新上去,也就完成了。
实际操作时也不需要每次更新都推上去,只要把四个tmp维护好,最后Dfs走一边就更新完了。
如图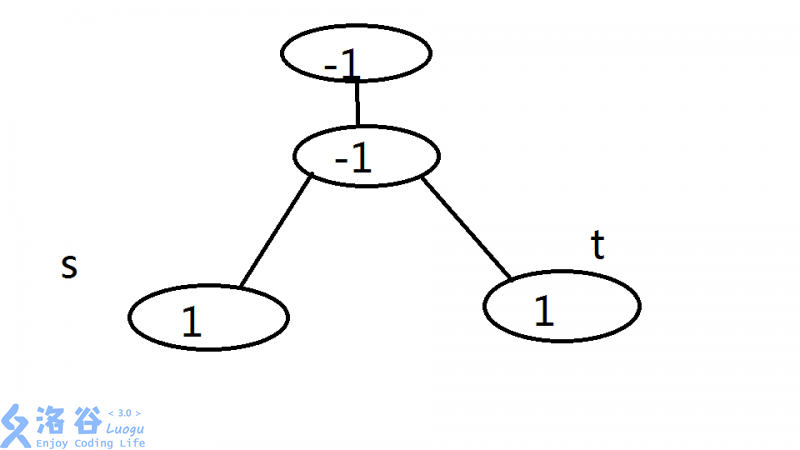
总结:
点权求和:若[x,y]两点之间路径上的所有点的权值+d,则w[x]+=d , w[y]+=d , w[LCA(x,y)]-=d , w[Fa[LCA(x,y)]]-=d
边权求和:若[x,y]两点之间路径上的所有边的权值+d,则w[x]+=d , w[y]+=d , w[LCA(x,y)]-=d*2
三 边的差分和点的差分的关系
貌似 dian[i] = bian[i]+lcacnt[i]