介绍Simplify如何简化解码逻辑。
1. 使用
Simplify在DecodeLogic中使用,如下:

简化从t和dc项中查找的逻辑。
其方法签名如下:

其中:
a. minTerms: 卡诺图中的最小项;
b. dcTerms:卡诺图中的无关项;
c. bits:最小项中变量的个数;
2. 主要过程
Simplify定义如下:

主要步骤如下:
1) 从minTerms和dcTerms中获取质项,即在卡诺图中画圈,把最小项和无关项划入圈中,以合并最小项;
2) 从质项中查找必要质项,做出如下区分:
a. 把质项分为必要质项和非必要质项;
b. 把最小项(minTerms)分为必要质项覆盖的最小项和未覆盖的最小项;
c. 从非必要质项中提取出代价最小的能够覆盖未覆盖最小项的质项,并与必要质项合并为cover;
3) cover就是能够覆盖minTerms的最简项的集合;
3. 获取质项:getPrimeImplicants
调用方式如下:
把最小项和无关项合在一起进行化简,如卡诺图中把无关项合在一起进行画圈。
getPrimeImplicants的实现如下:

1) 合并之前,所有的最小项都是质项。即初始情况下,所有的最小项都是质项,互相不包含(cover);
2) 把所有项分布到一个bits x bits的表中;
若bits=4,表格如下:
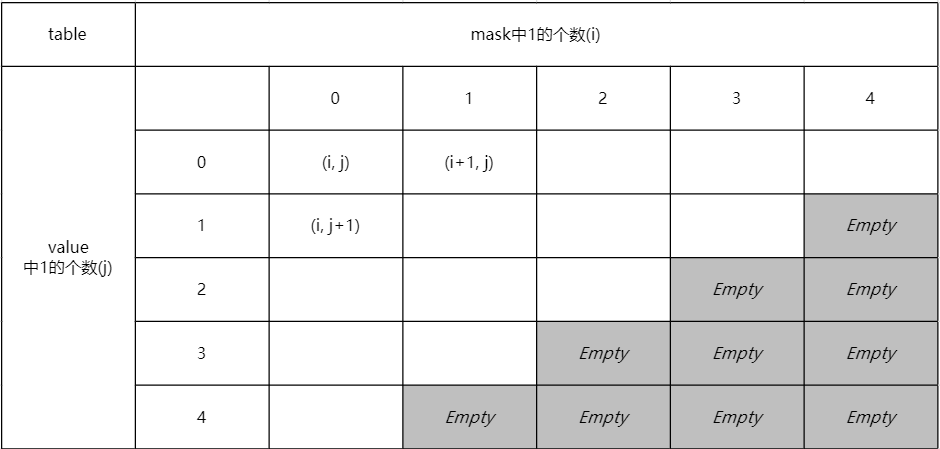
a. 先根据mask中比特位值为1的位的个数,把所有的蕴含项划分为5列;
b. 然后根据value中比特位值为1的位的个数,把所有列划分为5行;
由mask的意义可知:
a. 如果mask中1的个数为0,则value中最多可以有4个1;
b. 如果mask中1的个数为1,则value中最多可以有3个1;
所以每一列中,有一些单元格为空,没有蕴含项分布。
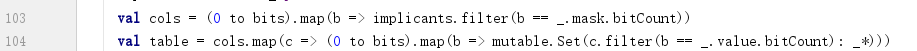
3) 把单元格(i, j)和(i, j+1)中的蕴含项合并之后存入单元格(i+1, j)
单元格(i, j+1)中的项与单元格(i, j)中的项相比,mask中1的位数相同,value中1的位数多了一个,即符合Term.similar的初步特征;
如果判断出有similar的项,则可以将二者merge。合并生成的新项相较于(i, j+1),value中1的位数减少一个,mask中1的位数增加一个,即应当存入单元格(i+1, j)。
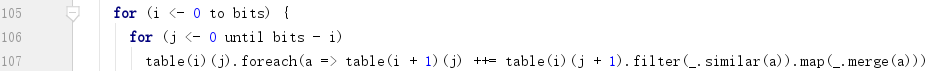
4) 搜集未被合并的质项

5) 把所有质项进行排序

举例如下:

也就是说primes中primes(0)“最小”。
primes(0)相较于primes(1),具有这样的倾向:value中的1更少,或者mask中的1更少。
只是倾向,而非绝对。
6) 所有最小项都被质项覆盖

4. 获取必要质项
调用方式如下:
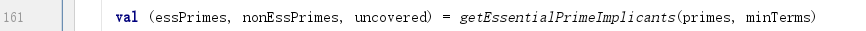
从质项中查找必要质项,即含有不被其他任何项包含的子项的质项。
getEssentialPrimeImplicants实现如下:
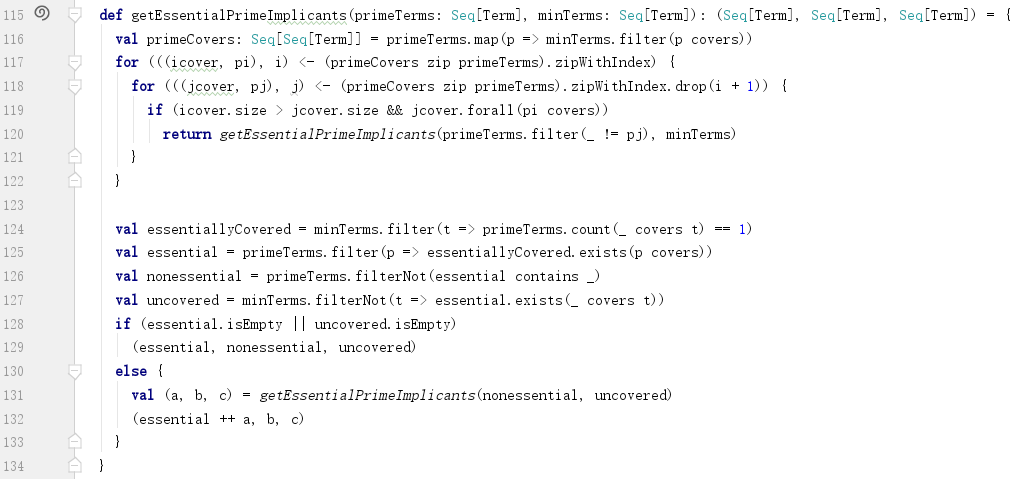
1) 获取每一个质项覆盖的最小项

可以使用如下表格演示:
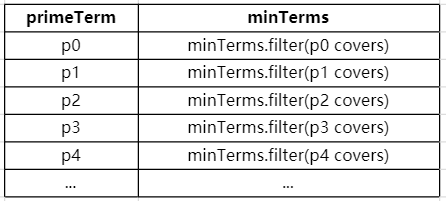
2) 移除可以省略的质项

把(p0, p0CoverdMinTerms)与(p1, p1CoveredMinTerms)进行对比,如果p0覆盖的最小项多,并且p0覆盖p1覆盖的所有最小项,则p1不是必要质项。
再把(p0, p0CoverdMinTerms)逐个与(p2, p2CoveredMinTerms),(p3, p3CoverdMinTerms)等进行对比。
然后是把p1与p2,p3等进行对比。
因为比对的方法是:

不存在else处理,所以这里存在一个假设:p0覆盖的最小项比p1的多。
这样就依赖于primes.sortWith(_ < _)这个动作,而这个排序动作无法保证这个假设。
所以这里无法保证primeTerms是最简的。
3) 获取必要质项覆盖的最小项
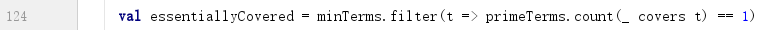
只被一个质项覆盖的最小项,所对应的质项一定是必要质项。但这不是必要质项的全部。
4) 把质项分为必要质项和非必要质项两部分

5) 获取未被必要质项覆盖到的最小项
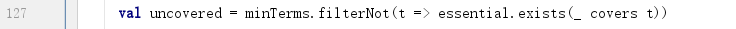
6) 判断是否找到全部必要质项
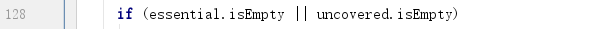
a. 如果所有最小项已经全部被覆盖(uncovered.isEmpty),则已经找全;
b. 如果没有找到必要质项,则所有质项都是非必要质项,无需再找;
7) 如果只是找到一部分必要质项,而尚有一部分最小项没被覆盖。则在非必要质项中继续查找针对uncovered的必要质项。

直至6)中的条件为真。
可以看到getEssentialPrimeImplicants终止有两种情况:
a. 找到全部必要质项,uncovered为空;
b. 没找到全部必要质项,uncovered不为空。而余下的非必要质项每一个都覆盖2个以上的最小项;
5. 获取cover
如果没有找到全部必要质项,uncovered不为空。则需要从剩余的非必要质项中,选出能够以最小的代价覆盖uncovered的质项。
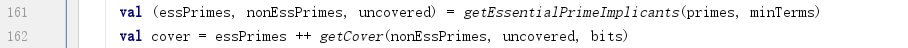
getCover实现如下:

这里看minTerms也就是uncovered不为空的情况。
1) 获取每个最小项对应的蕴含项
如下表:
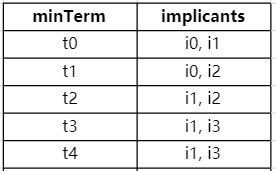
每个蕴含项至少覆盖2个最小项;
2) 获取能覆盖全部最小项的蕴含项组合
执行示例:
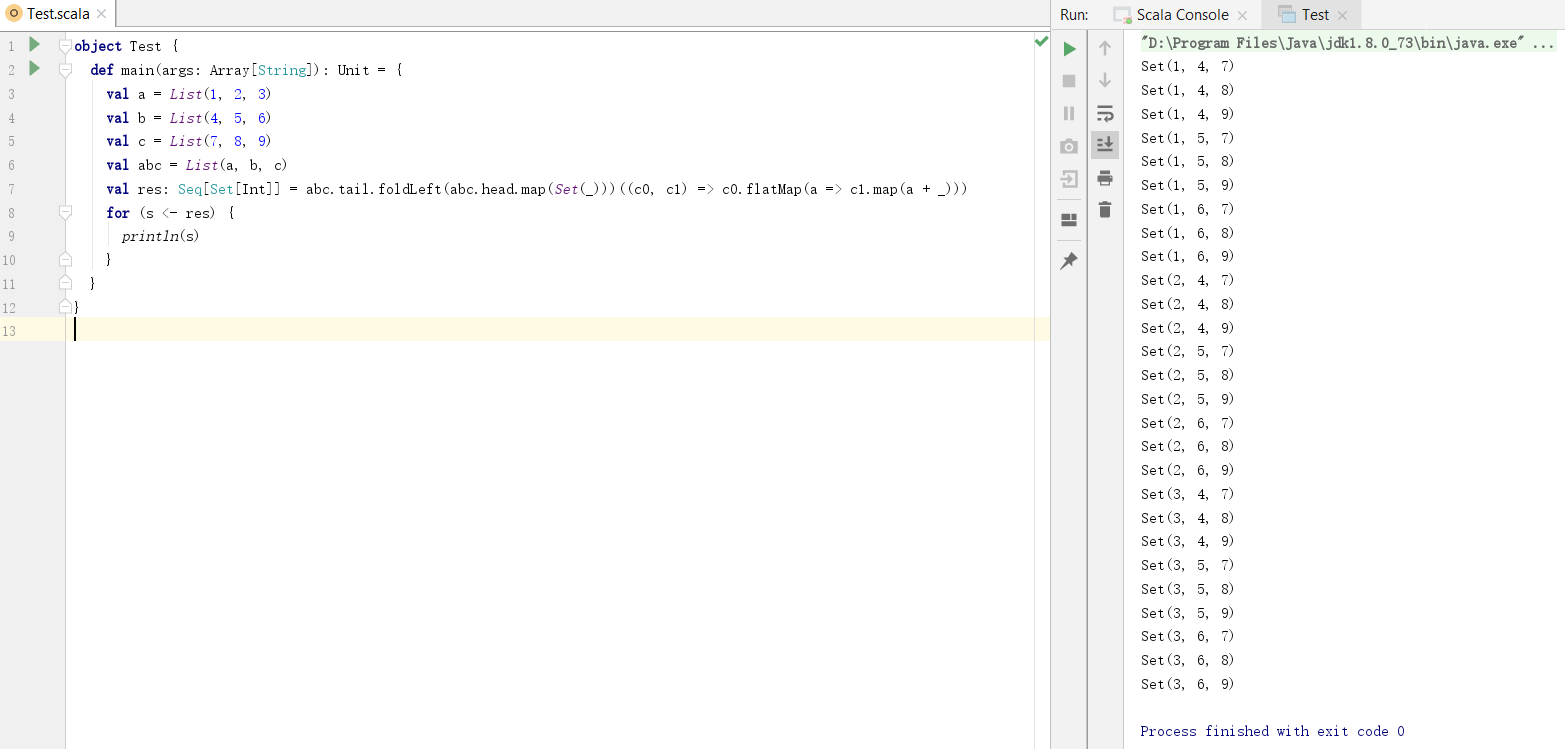
a. 把最小项t0对应的蕴含项分别放入集合中:cover.head.map(Set(_))
之所以用Set,是为了去重。
b. 把t1对应的蕴含项分别加入到t0生成的集合中:c0.flatMap(a => c1.map(a + _))
c1.map(...)每次都生成一个新的集合,这样生成的集合的数量成指数级增长。最终获取到能覆盖全部最小项的所有蕴含项组合。
3) 比较所有蕴含项组合,选择最cheaper的组合使用
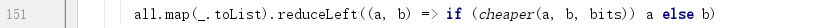
4) cheaper

简单来说,就是组合中使用的变量最少。
6. 确保所有最小项都得以覆盖