前言
树状数组最开始学的时候因为整不明白,所以就只是知道怎么用,网上很多人对着结论口胡树状数组的原理,印象不是特别深刻。后来重新学习了一遍,看了下知乎关于树状数组的讨论,希望能深入了解树状数组的原理,但是真的有点难理解,而且说法和思想有好几种,有的地方有可能还不够严谨,希望看完能对你有所启发
引入
假设我们有个一维数组,要进行两种操作:
1.修改某个元素
2.求指定区间的和
对于这个问题,我们有两种简单的解法
- 修改元素$i$直接通过下标访问($O(1)$),求区间和就按照区间进行累加($O(n)$)
- 先进行前缀和预处理,$sum[r]-sum[l-1]$得到区间和($O(1)$),但是修改元素$i$,就要把$i$之前的前缀和都更新($O(n)$)
可以看出两种方法各有优劣,一类折中的思路是同样存储一些区间内的计算结果,节省求和的时间,但尽量减少重叠区间的数量,从而减少更新的次数。
原理
如何高效的统计和修改数组内的信息呢?我们可以想到用树形结构
如果只需要查询前缀和的话,在线段树上查询是不需要用到右儿子的值的(如果要用,那么左儿子的值会被用到,那么还不如用父亲节点的值),所以去掉所有右儿子,就得到了树状数组的结构,如图:
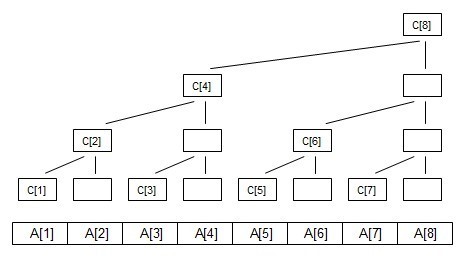
而我们可以把这里的$lowbit$理解为树的高度。观察下可以发现对于位置 $i$,其对应的结点所在的高度就是 $lowbit(i) $的位数,第一层是所有$lowbit(i)=1$的节点,第二层是所有$lowbit(i)=2$的节点······
节点的高度又决定了其子树的大小,因此对于节点$i$,它所维护的信息区间为$(i-lowbit(i),i]$
对于区间查询,我们是用右边界前缀和减去左边界前缀和得到。
由于任何正整数都能表示为2的幂相加的形式,那么求前缀和可以由多个长度为2的幂的区间的和得到。比如$19=2^{4}+2^{1}+2^{0}$,就是由前16个元素的和,再往后两个元素的和,再往后一个元素相加得到。那么我们可以不断去掉二进制末尾的1,统计对应区间的信息进行相加就可以了。
至于单点修改,理解起来可能稍微难懂一点(个人观点)
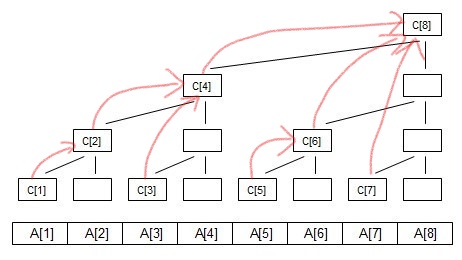
由于树形结构维护区间信息,那从这个节点往父节点走一直走到根节点,路径上的节点都要修改。关键在于如何找到父节点,其实对于当前节点$i$,它下一个存在的父节点就是$i+lowbit(i)$,为什么呢?
留坑吧,发现之前的证明存在问题
实现
了解了树状数组的原理后,想必实现起来思路就会清晰很多
int lowbit(int x){ return x&(-x); } //区间求和 int sum(int x){ int ret = 0 while(i){ ret += c[x]; x -= lowbit(x); } return ret; } //单点修改 void update(int x, int val){ while(x<=n){ c[x] += val; x += lowbit(x); //向上更新 } }
这里解释下$lowbit(i)$为什么可以用$i&(-i)$表示,计算机中的负数用对应正数的补码(正数取反加一)来表示
假设这里的$i$我表示成xxxxx100,那么$-i$就是#####011+1 = #####100(这里的#表示对x取反)
那么(xxxxx100)&(#####100) = 00000100,就是$i$的二进制的最低位1对应的值
Reference: