Contest Info
| Solved | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| 9/10 | O | Ø | Ø | O | - | O | Ø | O | Ø | Ø |
- O 在比赛中通过
- Ø 赛后通过
- ! 尝试了但是失败了
- - 没有尝试
Solutions
B.牛牛的DRB迷宫II
题意:
在限制条件下构造一个$n*m$的迷宫使得从左上角$(1, 1)$走到右下角$(n, m)$的路径数目刚好为$k$
思路:
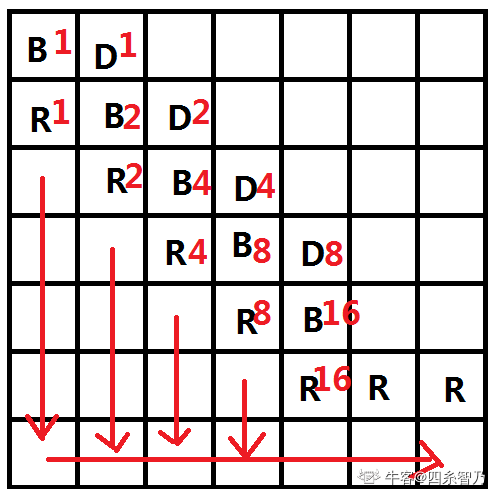
我们可以用拆位的思想,将$k$的二进制按位进行拆解。比如$19$我就可以写作$10011=2^{4}+2^{1}+2^{1}$,我们只要能得到$2^{x}$的构造,其他的数当然也能被构造出来。
接着可以构造一个二进制编码器,斜对角线上的方案数恰好是$1,2,3,4,8,16,32...$,只要这个数二进制某位上是$1$,我们就在其对应的二进制方案数上开一条向下的通道就可以了(R->B, 向下依次都变成U,最后一行都是R向右求和,毕竟是个二进制编码器嘛)
C.牛牛的数组越位
模拟,给不同的情况打上标记。比赛时候$WA$是因为只用了一个标记记录两种情况,然后那个标记就在两种情况下轮流赋值就出现错误

#include <cstdio> #include <cstring> #include <algorithm> #include <queue> #define ll long long using namespace std; const int maxn = 2e7+100; ll T, n, m, p, x, y, c; ll a[maxn]; int main(){ scanf("%lld", &T); while(T--){ scanf("%lld%lld%lld", &n, &m, &p); ll lim = n*m-1, fg = 0; for(int i = 0; i <= lim; i++) a[i] = 0; while(p--){ scanf("%lld%lld%lld", &x, &y, &c); if(x<0||x>n-1||y<0||y>m-1) fg = 1; ll tmp = m*x+y; if(tmp>=0&&tmp<=lim) a[tmp] = c; else fg = 2; } if(fg==2) printf("Runtime error "); else if(fg==1){ for(int i = 0; i <= lim; i++){ if((i+1)%m==0) printf("%d ", a[i]); else printf("%d ", a[i]); } printf("Undefined Behaviour "); } else{ for(int i = 0; i <= lim; i++){ if((i+1)%m==0) printf("%d ", a[i]); else printf(" %d", a[i]); } printf("Accepted "); } } }

#include <cstdio> #include <cstring> #include <algorithm> #include <queue> #define ll long long using namespace std; const int maxn = 2e7+100; int T, n, m, p, x, y, c; int a[maxn]; int main(){ scanf("%d", &T); while(T--){ scanf("%d%d%d", &n, &m, &p); ll lim = n*m-1, fg1 = 0, fg2 = 0; for(int i = 0; i <= lim; i++) a[i] = 0; while(p--){ scanf("%d%d%d", &x, &y, &c); if(x<0||x>n-1||y<0||y>m-1) fg1 = 1; ll tmp = m*x+y; if(tmp>=0&&tmp<=lim) a[tmp] = c; else fg2 = 1; } if(fg2) printf("Runtime error "); else{ for(int i = 0; i <= lim; i++){ if((i+1)%m==0) printf("%d ", a[i]); else printf("%d ", a[i]); } if(fg1) printf("Undefined Behaviour "); else printf("Accepted "); } } }
D.牛牛与二叉树的数组存储
同C题模拟

#include <cstdio> #include <cstring> #include <algorithm> #define ll long long using namespace std; const int maxn = 1e5+100; int n, cnt; int a[maxn<<1], id[maxn<<1]; int main(){ scanf("%d", &n); for(int i = 1; i <= n; i++){ scanf("%d", &a[i]); if(a[i]==-1) continue; id[a[i]] = i, cnt++; } a[0] = -1; for(int i = n+1; i <= 2*n+1; i++) a[i] = -1; printf("The size of the tree is %d ", cnt); printf("Node %d is the root node of the tree ", a[1]); for(int i = 1; i <= cnt; i++){ int rt = id[i]; printf("The father of node %d is %d, the left child is %d, and the right child is %d ", i, a[rt>>1], a[rt<<1], a[rt<<1|1]); } }
J.牛牛的宝可梦Go
题意:
给定权值全为1的$m$条道路连通$n$个城市,在特定时间$t$,地点$p$会出现价值为$val$的宝可梦,且保证同一时间点不会出现两只宝可梦。起始位置为1号城市,起始时间为0时刻,问他能捕获的宝可梦价值之和最大为多少
思路:
既然需要在不同城市间移动,想尽可能多的捕获宝可梦,那么就需要走最短路,首先跑一遍$Floyd$,得出各点对间的最短路
接下来就需要选择我们捕获的宝可梦,那我们去捕捉哪些宝可梦才能使得价值之和最大了呢?
我们定义$dp[i]$为最后捕获的宝可梦为$i$的最大价值,那当前状态可以由此时刻前最后捕获的宝可梦为$j$的最大价值转移得到,
$dp[i] = dp[j] + val[i]$
当然前提是我能在$i$出现前赶到他所在的地点,即$dis[i][j]<=t[i]-t[j]$
为了更方便的转移,我们可以把这些宝可梦按出现的时间进行排序,这样就可以快速遍历此时刻前捕获的宝可梦们了
但是你这个时候会发现一个问题,我照这样去转移的话,时间复杂度为$O(n^{2})$,肯定会超时。实际上从最近200个开始转移就可以了,因为200个以外的,都距离超过200个时间了(只有200个城市),必能走到。这样就把复杂度从$O(n^{2})$降到了$O(200*n)$
由此可以得到,$0到i-200$这些都能直接转移,我们只需要记录最大值$maxval$, 最后将$maxval+val[i]$和$i-200$到$i$转移后的最大值进行比较就可以了。
注意!!!$dp$数组初始化为$-inf$。因为题目要求人一开始在1号点,所以一开始可能有点赶不过去, $-inf$保证了起点是1号点
比如,排序后有宝可梦1、2、3、4,这时1、2都不能到达,假如3此时从2转移,如果$d[2]$为0的话,那么$dp[3]$就会更新为$val$, 但是明明就不能从1到2,根本就不存在1->2->3这条路径

#include <cstdio> #include <cstring> #include <algorithm> #define ll long long using namespace std; const int maxn = 210, maxm = 1e5+100; int n, m, k, x, y, dis[maxn][maxn]; ll dp[maxm], ans; struct node{ int t, p, val; }a[maxm]; bool cmp(node a, node b){ return a.t < b.t; } int main(){ scanf("%d%d", &n, &m); memset(dis, 0x3f, sizeof(dis)); for(int i = 1; i <= n; i++) dis[i][i] = 0; while(m--){ scanf("%d%d", &x, &y); dis[x][y] = dis[y][x] = 1; } for(int k = 1; k <= n; k++) for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) dis[i][j] = min(dis[i][j], dis[i][k]+dis[k][j]); scanf("%d", &k); for(int i = 1; i <= k; i++)scanf("%d%d%d", &a[i].t, &a[i].p, &a[i].val); sort(a+1, a+1+k, cmp); a[0].p = 1; //初始位置为1, 时刻为0 for(int i = 1; i <= k; i++) dp[i] = -1ll<<33; for(int i = 1; i <= k; i++){ for(int j = i-1; j >= max(0, i-200); j--) if(dis[a[i].p][a[j].p]<=a[i].t-a[j].t) dp[i] = max(dp[i], dp[j]+a[i].val); ans = max(ans, dp[i]); //这里的ans就相当于maxval } printf("%lld", ans); return 0; }
(这题的价值应该在于$dp$的应用,作者提到和求最长上升子序列问题的过程类似,至于最短路只是求个路径而已,反正历次比赛我$dp$的定义和转移就基本想不到)
References:
