前言
每次比赛总是有那么几个搞数据结构的题目,从最开始了解的单调栈,单调队列,线段树再到后来的主席树,树链剖分,后缀自动机,虽然有的还没有学,看来数据结构没我想的那么好搞,光是搞懂一个新的知识点就要花点功夫,慢慢做题就会发现,其实数据结构还是难在加上思维去运用。
主席树据说是一个叫黄嘉泰的同学发明的,至于为啥叫“主席树呢”,你看下这位大佬的缩写$(HJT)$是不是我们历届哪位主席,是吧,咋们不敢说也不敢问
抛出问题
给定$N$个数,共有 $M$次询问,每次都要询问区间 $[l,r]$的第 $k$大的数。其中 $N,M,l,r$均不超过$2 imes 10^{5}$ ,保证询问有答案。
解决问题
暴力法
显而易见,最暴力的办法就是区间排序然后输出排序后第$k$个数。最坏情况的时间复杂度是$ O(nmlgn)$,不超时才怪。
主席树(可持久化线段树)法
于是针对这个问题,新的数据结构诞生了,也就是主席树。
主席树本名可持久化线段树,也就是说,主席树是基于线段树发展而来的一种数据结构。其前缀"可持久化"意在给线段树增加一些历史点来维护历史数据,使得我们能在较短时间内查询历史数据。
我们先来看一段话来了解下主席树
首先,学习主席树要点的前置技能是权值线段树。权值线段树之所以会带上“权值”二字,是因为它是记录权值的线段树。因此需要用到离散化操作来处理a[1-n]。记录权值指的是,每个点上存的是区间内的数字出现的总次数。比如一个长度为10的数组[1,1,2,3,3,4,4,4,4,5]。
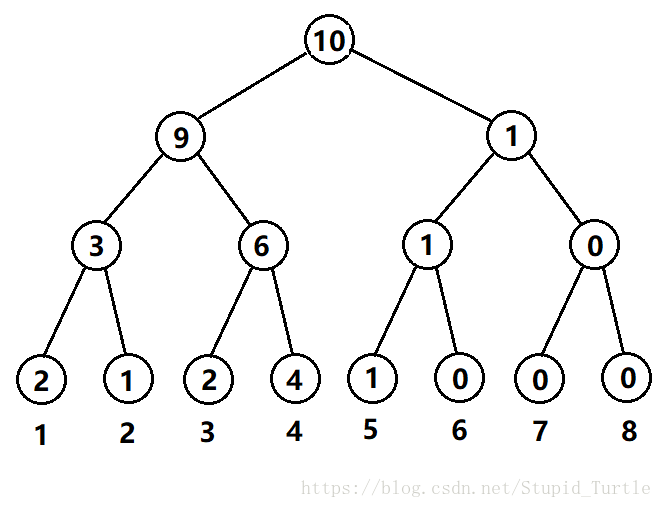
其中1出现了两次,那么[1,1]这个节点的值为2,2出现了1次,那么[2,2]这个节点的值为1,那么显然[1,2]这个节点的值为3,即1出现的次数和2出现的次数加和。那么如果我想要知道这个数组上的第k小,我就可以在这棵权值线段树上用logn的时间来实现。比如我想要求这个区间上的第7小,那么我先找到这棵树的根节点,根节点上的数字显示的是10,表示在[1,8]这个区间上一共有10个数字,那么我只要去看它的左孩子上的个数是多少。这时我看到左孩子上的数字是9,说明前9小的数字都在左子树上,那么我要找的第7小也在左子树上,那么我就递归去找左子树。当我再看左孩子的时候,看到数字是3,说明前3小的数字在左子树上,那么我要找的就是右子树上的第k-sum[i]小,即7-3=4,找到右子树上的第4小即可。直到找到某一个叶子节点,说明找到了我要找的第k小。这是通过权值线段树找到区间[1,n]上的第k小/大的应用。
那么知道了权值线段树是什么之后,主席树又是什么呢。主席树是一棵可持久化线段树,可持久化指的是它保存了这棵树的所有历史版本,最简单的办法是:如果你输入了n个数,那么每输入一个数字a[i],就构造一棵保存了从a[1]到a[i]的权值线段树。之所以这么做,是因为我们可以把第j棵树和第(i-1)棵树上的每个点的权值相减,来得到一颗新的权值线段树,而这个新的权值线段树相当于是输入了a[i]到a[j]以后得到的。如果这么说不太好理解的话,我们可以思考另外一个模型:求数组a[1]到a[n]的和。如果只是求[1,n]这一段的和,那么我们直接全部加起来就可以了,或者求一个前缀和sum[n]即可。那么如果我给定了l和r,想要知道[l,r]这段区间上的和呢?是不是利用前缀和sum[r]-sum[l-1]就可以轻松得到?那么主席树的思想也是如此,将tree[r]-tree[l-1]得到的一棵权值线段树即为属于[l,r]的一棵权值线段树,那么在这么一棵权值线段树上求第k大不是就转变为之前的问题了么。如果还是没有理解为什么可以用tree[r]-tree[l-1]来表示属于[l,r]的权值线段树,可以自己构造一个数组,然后画出属于[1,l-1],[1,r]和[l,r]的三颗权值线段树,来自己研究研究,多自己动手也不是一件坏事嘛。
想必看到这里你对主席树应该有了大概的印象
接下来我们先看道权值线段树的例题:[NOI2004]郁闷的出纳员
说起权值线段树,其实写完后发现真的和线段树差不多,线段树维护的是下标区间内的信息,而权值线段树维护的是权值区间内的信息,例如维护权值属于[2,7]这个区间中各个数出现的次数
本题维护一个偏移量$infu$,当 $A$ 操作时,加工资$ infu+=x$;$S$ 操作 $infu-=x$,这时有区间修改,低于最低工资的要清0 。注意在有新员工插入的时候加入$x -infu$即可,这样仍然是全局偏移量
所有数据在处理的时候都要加上$base$,$base$ 是防止负数出现
Code

#include <cstdio> #include <algorithm> #define lson rt<<1, l , mid #define rson rt<<1|1, mid+1 , r using namespace std; const int maxn = 4e5 + 20; const int base = 2e5 + 10; int n, mink, k; char ch; int tree[maxn<<2], lazy[maxn<<2]; void push_up(int rt){ tree[rt] = tree[rt<<1] + tree[rt<<1|1]; } void push_down(int rt){ if(!lazy[rt]) return; tree[rt<<1] = tree[rt<<1|1] = 0; lazy[rt] = 0; lazy[rt<<1] = lazy[rt<<1|1] = 1; } //单点修改 void insert(int rt, int l, int r, int pos){ if(l==r){ tree[rt]++; //tree[rt]才代表区间[pos,pos]节点的值 return ; } push_down(rt); //单调修改也需要push_down, 不然会WA(废话) int mid = (l+r)>>1; if(pos<=mid) insert(lson, pos); else insert(rson, pos); push_up(rt); //其实用tree[rt]++也可,这点在主席树里面会有所体现 } //区间修改 void update(int rt, int l, int r, int ul, int ur){ if(ul<=l&&r<=ur){ tree[rt] = 0; lazy[rt] = 1; return ; } push_down(rt); int mid = (l+r)>>1; if(ul<=mid) update(lson, ul, ur); if(ur>mid) update(rson, ul, ur); push_up(rt); } //全区间查询第k大 int query(int rt, int l, int r, int k){ if(l==r) return l; push_down(rt); int mid = (l+r)>>1; if(tree[rt<<1|1]>=k) return query(rson, k); else return query(lson, k-tree[rt<<1|1]); } int main(){ scanf("%d%d", &n, &mink); int ans = 0, infu = 0; while(n--){ scanf(" %c%d", &ch ,&k); if(ch=='I'){ if(k<mink) continue; ans++; insert(1, 1, maxn, k-infu+base); //k-infu+base(注意读题,是当集体扣工资时才会有人离开公司) } else if(ch=='A') infu += k; else if(ch=='S'){ infu -= k; update(1, 1, maxn, 1, mink-infu+base-1); //x+infu<mink, x<mink-infu,区间是闭区间,所以 mink-infu+base-1 } else { if(tree[1]<k) printf("-1 "); else printf("%d ", query(1, 1, maxn, k)-base+infu); } } printf("%d ",ans-tree[1]); return 0; }
我们的前置技能点完了,下面正式来看我们又爱又恨的主席树

#include <cstdio> #include <algorithm> using namespace std; const int maxn = 4e6+10; int n, q, pntnum = 0;//pnt是Persistable_Segment_Tree的缩写 int a[maxn], b[maxn]; int rt[maxn], ls[maxn], rs[maxn], tree[maxn]; void build(int &pos,int l,int r){ //这里传的是&pos!!! pos = ++pntnum; if(l==r) return; int mid=(l+r)>>1; build(ls[pos],l,mid); build(rs[pos],mid+1,r); } //单点修改 void insert(int &pos,int vsn,int l,int r,int loc){//pos新版本的当前节点编号,vsn旧版本的当前节点编号,l左端点,r右端点,loc要修改的节点编号 pos = ++pntnum; //新增节点 if(l==r){ tree[pos]=tree[vsn]+1;//当前节点加1 return; } ls[pos]=ls[vsn]; //继承左子树 rs[pos]=rs[vsn]; //继承右子树 tree[pos]=tree[vsn]+1; //当前路径上的所有点权值加1,这里相当于push_up,只不过对于这道题直接在父节点写比较方便 int mid=(l+r)>>1; if(loc<=mid) insert(ls[pos],ls[vsn],l,mid,loc); else insert(rs[pos],rs[vsn],mid+1,r,loc); } //查询第k小 int query(int lv,int rv,int l,int r,int k){ if(l==r) return l; int mid=(l+r)>>1, sum = tree[ls[rv]]-tree[ls[lv]]; if(sum>=k) return query(ls[lv],ls[rv],l,mid,k); else return query(rs[lv],rs[rv],mid+1,r,k-sum); } int main(){ scanf("%d%d", &n, &q); for(int i = 1; i <= n; i++) scanf("%d", &a[i]), b[i] = a[i]; sort(b+1, b+n+1); int m = unique(b+1, b+n+1)-b-1; build(rt[0], 1, m); for(int i = 1; i <= n; i++){ int p = lower_bound(b+1, b+1+m, a[i])-b;//离散化映射 insert(rt[i], rt[i-1], 1, m, p); } while(q--){ int l, r, k; scanf("%d%d%d", &l, &r, &k); int ans = query(rt[l-1], rt[r], 1, m, k); printf("%d ", b[ans]); } return 0; }