2019牛客暑期多校训练营（第十场）J

>传送门<

题意

---

$n$个宽度为$w_{i}$,高为$h_{i}$ 的 木块，要求分成$k$组，对于每组内的所有木块，高度都变为组内最低木块的高度，宽度保持不变，求变化的最小面积。

分析

---

由于$dp$状态定义不同写法也不同，这里给出一种解法

高度比较高的木块为迁就高度比较低的(为了$dp$方程及其优化)，所以先把木板按照高度从高到低排序

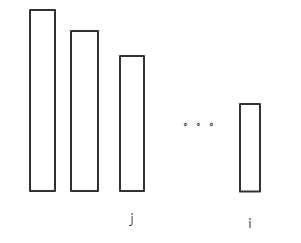
如果设$d[i][k]$ 为前$ i $个分成 $k $份可以保留的最大面积，那么答案就是 $tot−d[n][k]$（$tot$ 为初始总面积）

考虑如何转移

　　　　　　　　　　　　　　　$d[i][k]=max(d[j][k-1]+(pre[i]-pre[j])cdot h[i])$

其中$pre$为宽度前缀和，即$pre[i]=sum_{1}^{i}w[i] $。

暴力转移复杂度较高($O(n^{2})$)，考虑如何优化。（这不就是个斜率优化嘛）

我们设$j_{1}<j_{2}<i$且在计算$dp[i][k]$的时候，决策$j_{2}$更优，也就是说

　　　　　　　　　　　　　　　　$d[j_{1}][k−1]+(pre[i]−pre[j_{1}])cdot h[i]<d[j_{2}][k−1]+(pre[i]−pre[j_{2}])cdot h[i] $

这时$j_{1}$可以从决策集中被删去，因为后者的$j_{2}$要比$j_{1}$更优。

上式可以化简为

　　　　　　　　　　　　　　$frac{d[j_{2}][k-1]-d[j_{1}][k-1]}{pre[j_{2}]-pre[j_{1}]}$>$h[i]$

这时我们维护一个单调递减的决策集就可以了

Code

#include <bits/stdc++.h>
#define empty (head>=tail)
#define ll long long
using namespace std;
const int maxn = 5e3+10, maxk = 2e3+10;
int n, k, head, tail, j;
ll pre[maxn], d[maxn][maxk], q[maxn];
struct node{int w ,h;}a[maxn];
bool cmp(node a, node b){return a.h > b.h;}
long double slope(int x, int y, int p) {
    return (long double)(d[y][p-1]-d[x][p-1])/(pre[y]-pre[x]);
}
int main()
{
    scanf("%d%d", &n, &k);
    ll sum = 0;
    for (int i = 1; i<= n; i++) {
        scanf("%d%d", &a[i].w, &a[i].h);
        sum += a[i].h * a[i].w;
    }
    sort(a+1, a+1+n, cmp);
    for (int i = 1; i <= n; i++) pre[i] = pre[i-1] + a[i].w;
    for(int p = 1; p <= k; p++) {
        head = tail = 1;
        for (int i = 1; i <= n; i++) {
            while(!empty&&slope(q[head],q[head+1],p)>a[i].h) head++;
            j = q[head]; d[i][p] = d[j][p-1]+a[i].h*(pre[i]-pre[j]);
            while(!empty&&slope(q[tail],q[tail-1],p)<slope(q[tail],i,p)) tail--;
            q[++tail] = i;
        }
    }
    printf("%lld
", sum-d[n][k]);
    return 0;
}

思考

---

开始对木板高度排序那里，能想到的应该就直接想到了，没想到的应该是写转移方程的时候发现，排序后比较好写出转移方程，并且需要对其进行优化就会去关心排序的方向。原博主的博客一直都写的挺好的，但是我觉得这种东西还是要多看看各种博客，这会给你广阔的思路和一些对比。他有关斜率优化$dp$的题目里，写的都是由于$A[i]$是单调递增/递减，所以维护的是一个递增/递减的决策集，但是我在相关题目写的挺好的博客里看到的是，博主都是给出说明为什么维护一个凸包/凹包，而并没有说是因为上面的那种原因。另外这题，由于看过维护凸包的，类比的思想维护凹包原理上都是差不多的，不过之后还是要去写凹包相关题目(立flag)。遇到有困惑的地方，重新翻回去看大米饼的博客还有其他人的博客，感觉慢慢会清晰一点，$go on$~