题意:求最少需要多少个3的倍数按位或后可以得到数字a
思路:利用3的倍数对应的二进制数的性质来先选出一个x,然后根据数字a再配一个y出来
首先,我们都知道十进制中,任意一个数只要每一位相加的和能被3整除,那么这个数就能被3整除。
这是为什么?
因为十进制中每一个位都会10^k次方,那么仅仅是每一位%3的值都是余1,那么我们只要凑3个余1的,那么3就能被这个数整除。
这题思路一样,换成2进制,只要各个位置上的数mod 3后的和相加起来mod 3为0,则这个数就是3的倍数
接下来分类讨论下:
A. 如果a是3的倍数,那么我们直接取a即可
B. 如果a的二进制只有一位或两位,我们根本取不出0以外的三的倍数,所以无解。题目保证有解所以可以基本不考虑太多。
C. a的二进制位至少有三位的情况
首先明确一些性质
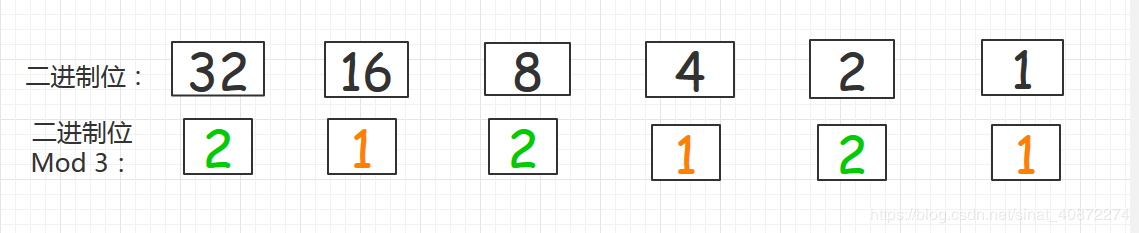
1.每一个二进制位mod 3 只能得到 1 或 2
2.每个mod 3 = 2 的数和 mod 3 = 1的数相加 一定是三的倍数
3.mod 3 后余数相同的数相减以后一定也是三的倍数
Ⅰ. 若a mod 3 = 1
如果a中的二进制位有至少两个mod 3 =1的,设它们为p和q,我们取{a-p,a-q}即可。
因为a,p 和 q 都是mod 3 = 1的,所以a-p和a-q必定是三的倍数。同时a-p和a-q等于将原本p,q处的1变成了0. 这样一来,a-p和a-q按位或之后就还是a
举个例子: a = 19
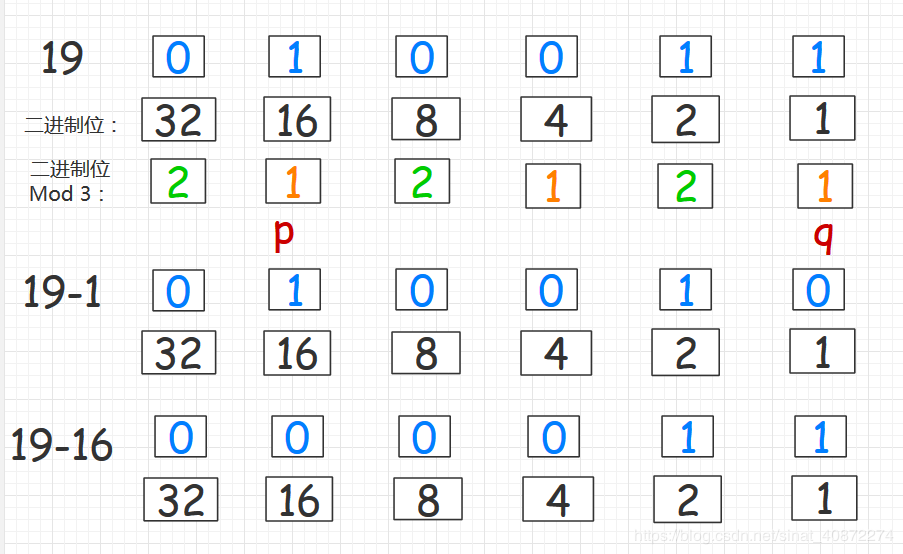
如果a中的二进制位有恰好一个mod3=1的,那么设mod3=1的这个位为p,mod3=2的某个位为q,我们取{a-p,p+q}即可。
a-p的道理同上,p+q 因为一个mod 3 = 1,一个 mod 3 = 2 所以两者加起来一定是三的倍数,同时p+q与a-p按位与一定是a,因为a-p去掉的p p+q给补上了 多出的q是原本a中就有的所以没有什么影响。
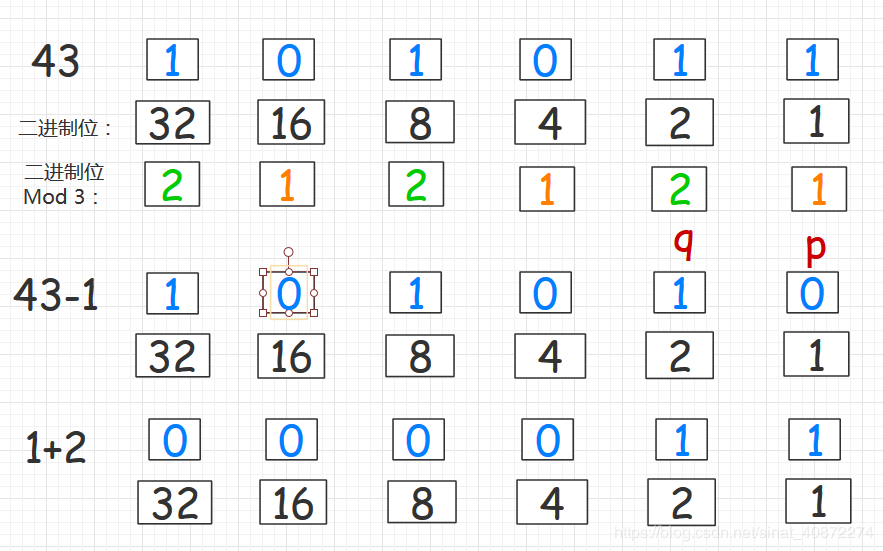
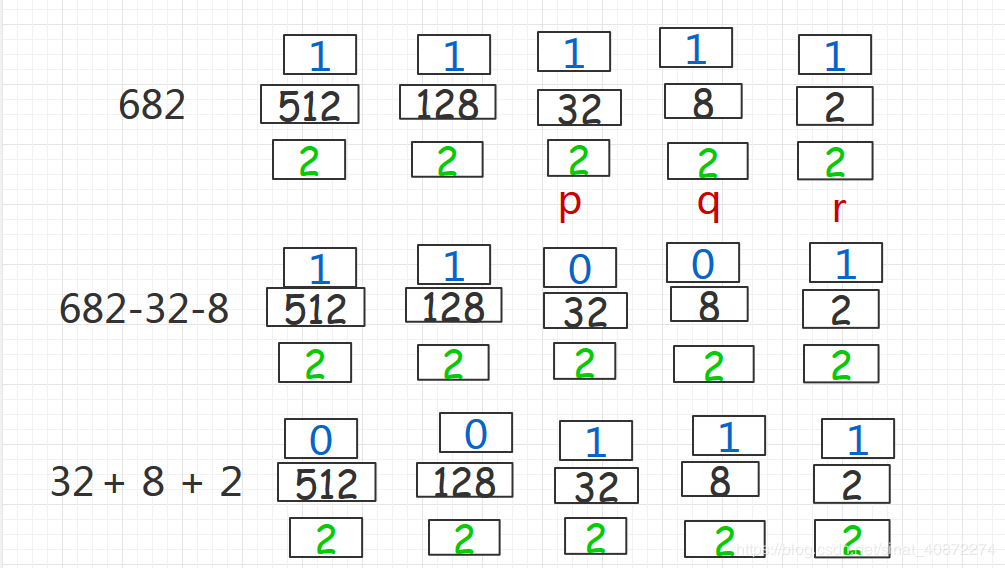
如果a中的二进制位没有mod3=1的,那么假设有三个mod3=2的位p,q,r,我们取{a-p-q,p+q+r}即可。
因为p和q都是mod 3 = 2,所以p+q mod 3 = 1,就和 a 是一样的了 故 a-p-q是三的倍数,又因为r也是 mod 3 = 2,所以q+p+r 原本是mod 3 = 6 ,6可以除尽3,所以q+p+r 也是三的倍数
Ⅱ.若a mod 3 = 2
只需把上面的讨论中1与2互换即可,是完全对称的
Code

#include<bits/stdc++.h> using namespace std; typedef long long ll; ll a; void solve() { scanf("%lld",&a); vector<ll> bb[2]; for(int i=0;i<=60;i++) if((a>>i)&1) bb[i&1].push_back(1LL<<i); //记录每一个1的位置和保存他的奇偶 if(a%3==0) printf("1 %lld ",a); //本身 else if(bb[1].size()+bb[0].size()<=2) return;//凑不出 (这里可能需要稍微仔细体会下) else{ ll x,y; int s = (a%3==2); //余数是2还是1 if(bb[s].size()){//如果原数里有我们需要的,可以直接减去的 x = a-bb[s][0]; if(bb[!s].size()) y = (bb[s][0]) + (bb[!s][0]); //凑3的两种方式 else y = a - bb[s][1]; }else{ //原数里没有余数 x = a-(bb[!s][0]+bb[!s][1]); y = bb[!s][0]+bb[!s][1]+bb[!s][2]; } printf("2 %lld %lld ",x,y); } } int main() { int T; cin>>T; while(T--){ solve(); } return 0; }
参考自:
https://blog.csdn.net/sinat_40872274/article/details/97551579
https://blog.csdn.net/A_Pathfinder/article/details/97612078
(建议对着这两篇博客一起看)
