之前因为各种原因没看数学相关问题,这回牛客网44练习赛打完或回头来看发现还是要看一下才行,不然有点摸不着头脑
1.素数判定
给定正整数n,请判断n是不是素数

bool is_prime(ll n) { for (int i = 2; i*i <= n; i++) if (n%i==0) return false; return n!=1; }
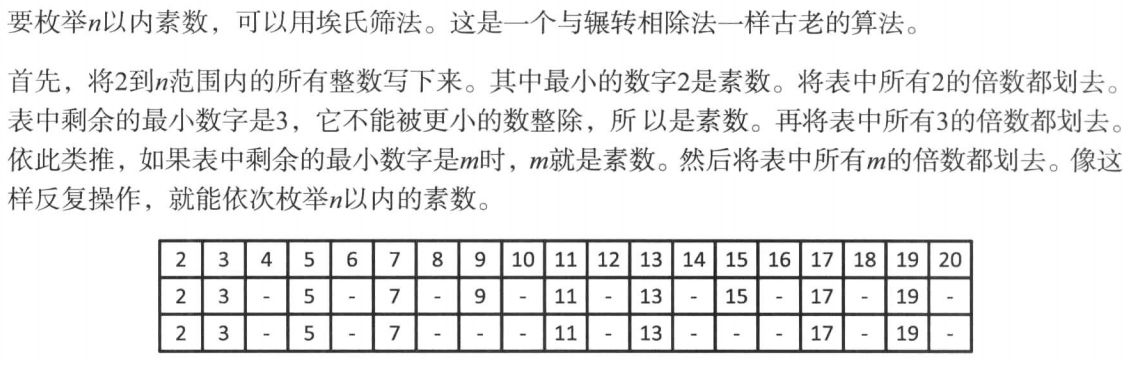
2.埃氏筛法
给定正整数n,请问n以内有多少个素数?
int prime[MAX_N]; //第i个素数 bool is_prime[MAX_N+1]; //值为true表示为素数 //返回n以内的素数 int sieve(ll n) { int p = 0; for (int i = 0; i <= n; i++) is_prime = true; //is_prime[0] = is_prime[1] = false; for (int i = 2; i<= n; i++) { if (is_prime[i]) { prime[p++] = i; for (int j = 2*i; j <= n; j += i) is_prime[j] = false; } } return p; }
3.区间筛法
给定正整数a和b,请问区间[a,b)又多少个素数?

typedef long long ll; bool is_prime[MAX_L]; bool is_prime_small[MAX_SORT_B]; //对区间[a,b)内的整数执行筛法 void segment_sieve(LL a,LL b) { for(int i = 0; (LL)i*i < b; i++) is_prime_small[i]=true; for(int i = 0; i < b-a; i++) is_prime[i]=true; //利用0~len代表a~b的数 for(int i = 2; (LL)i*i < b; i++) { if(is_prime_small[i]) { for(int j = 2*i; (LL)j*j < b; j += i) is_prime_small[j]=false; //筛[2,√b) for(LL j=max(2LL, (a+i-1)/i)*i ; j < b; j+=i) is_prime[j - a] =false;//筛[a,b) //j代表素数,j-a是将a~b变为0~b-a以便数组好存储 //2LL是2的长整形形式,与其比较意思是j最少是i的两倍 //((a+i-1)/i)*i得出的是(>=a && %i==0)离a最近的数,这里分子上a-1是个小细节 //其实也可以写成a%i==0?a:(a/i+1)*i } } }