SIGAI机器学习第十八集 线性模型2

之前讲过SVM，是通过最大化间隔导出的一套方法，现在从另外一个角度来定义SVM，来介绍整个线性SVM的家族。

大纲：

线性支持向量机简介
L2正则化L1-loss SVC原问题
L2正则化L2-loss SVC原问题
L2正则化SVC对偶问题
L1正则化L2-loss SVC原问题
多类线性支持向量机
实验环节
libsvm和liblinear的比较
实际应用

线性支持向量机简介：

 不带核函数的预测函数是sgn(w^Tx+b)的形式，w是所有支持向量的组合，展开之后是sgn(Σ1~l a_iy_ix_i^Tx_i+b)的形式（l是训练样本数，a_i是支持向量的系数，y_i是第i个样本的类别标签，如果加上核函数是一个核函数的映射模型k(x_i^Tx_i)），现实世界中很多问题都是非线性问题，所以用非线性的支持向量机，用RBF或多项式核得到的模型更精确一些对于分类问题准确率更高，但是用这种非线性核在计算的时候运算量太大(先支持向量x_i做内积再做核映射，然后再乘以系数加起来，这对于大规模问题运算量是相当大的)。对于工业上的一些应用，特征向量的维数可能是1亿数量级，样本数可能也有1亿数量级，用这种非线性核来做的话显然是不现实的，在速度上达不到我们的要求，所以线性的支持向量机还是有它的用武之地的，虽然他还是线性的，但是他保留了线性支持向量机的优点，泛化性能非常好，他在允许一定错分的情况下最大化分类间隔，而且兼顾了速度，是一个不错的选择。

L2正则化L1-loss SVC原问题：

介绍第一种线性支持向量机，L2正则化L1-loss函数的支持向量机SVC（SVC是支持向量分类，用于分类问题，SVR是支持向量回归，用于回归问题）。

原问题为：

前边是正则化项，后边是一个损失函数（每个样本的损失累加起来）。

max(0, 1-y_iw^Tx_i)称为hinge loss，合页损失函数，即满足不等式约束y_iw^Tx_i≥1的损失等于0，不满足不等式约束的损失越厉害，损失就越厉害。

换元变换：

的形式同线性不可分的原问题的目标函数（其中的i/2wTw是为了最大化间隔而引入的，CΣξ表示错分以后给的一个惩罚），而这里1/2w^Tw是作为正则化项引入的，CΣξ这里表示同样的错分给一个惩罚损失，不等式约束（ξ≥0，ξ≥1-yiwTxi）就是线性不可分的原问题所要满足的约束（ξ是松弛变量，C是惩罚因子）。

 L2正则化L2-loss SVC原问题：

 

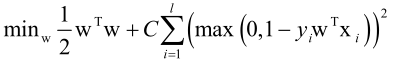
 可以用可信域牛顿法（是牛顿法的一个变种，也是寻找牛顿方向d，沿着d方向去迭代，总体的原理和前边讲的是一样的）求解，也可以转化成对偶问题求解。

L2正则化SVC对偶问题：

无论是L1损失函数还是L2损失函数，只要是L2正则化项的SVM，都可以通过拉格朗日对偶把它转化为以下形式的对偶问题：

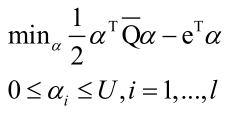
 和之前讲的一般SVM有一点类似，前边的目标函数形式上是一致的，只不过Q函数有一点不同。这里该目标函数的训练并没有SMO算法来求解，在liblinear中是用速度更快的坐标下降法来求解。每次挑出一个变量来进行优化把其他 变量固定住不动，则：

 

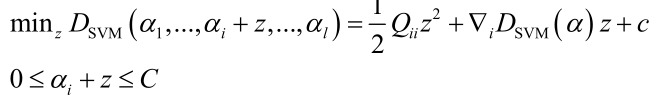
 优化a_i，其他变量保持不动，调整z使目标函数最下化，得到二次函数，和SMO一样可以得到公式解，需要考虑不等式约束，所以最后要做一个截断处理。

 L1正则化L2-loss SVC原问题：

 再介绍一种线性SVM，L1正则化的L2-loss损失函数的SVM，不过是损失函数是合页损失函数的平方：

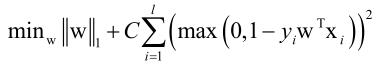
 可以用坐标下降法求解，效率是非常高的，　　

 

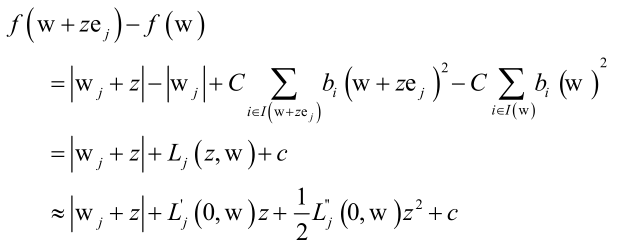
只调节w_j来进行优化，使得函数下降的最快，z是w_j的调整值，e_j是单位向量（如(0,0,1,0,0,...)）。最后用泰勒展开可以化为≈后的函数子问题可以采用牛顿法求解。

即坐标下降法外层循环依次优化w1、w2、...，内层循环用牛顿法求解一个子问题。

 多类线性支持向量机：

介绍最后一种线性的SVM，是多类的线性支持向量机。

libsvm里边采用一对一方案多个二分类的组合来完成多分类任务。这里直接优化一个多类的损失函数：

 第一项表示，如果有k个类，他就优化k个正则化项（这个正则化项可以理解为k个类的分类间隔），所以它本质上是一对剩余的方案，其实还是有k个二分类器。第二项是对不满足不等式约束的一个惩罚。

不等式约束：

表示属于yi的样本xi和属于yi那个类的分界线的权重系数做内积减去其他所有类的权重系数和xi的内积，ξ表示违反不等式约束的松弛变量即如果违反了就做一个惩罚。

分类的时候预测标准是：

 把x带到k个权重向量里做内积，看哪个最大就分到哪个类里边去，这实际就是一对剩余的方案，看哪个置信度高，离哪个而分类器边界越远，它就属于一类这边。

 可以把多分类的线性SVM用拉格朗日对偶转化一下，得到对偶形式的问题是：

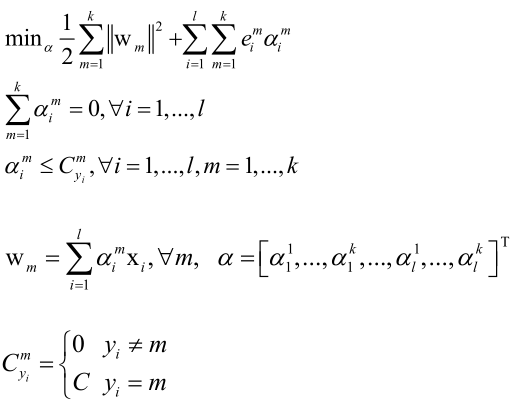
实际上还是先构造一个拉格朗日乘子函数出来，先固定住乘子变量，然后让原始要优化的变量w调整它们让目标函数取极小值，消掉w之后剩下a，调整a让目标函数取极大值就可以了。

这个对偶问题可以用（类似于坐标下降法这种思路）分治法求解。

实验环节：

同logistic回归，这里也是用liblinear做实验。

 train -s 3 a1a a1a_model_svm（-s 3表示某一种线性SVM，训练完模型保存到a1a_model_svm文件）

 执行，得到迭代次数169，支持向量个数608，目标损失函数最优值-540.863528。

打开生成模型的文件a1a_model_svm，里边内容是：

nr_class 2（类别数是2）
label 1 -1（标签值为1和-1，即二分类）
nr_feature 119（特征向量维数是119）
bias -1（偏置项-1）
w（权重向量，下边是w的分量...）
-0.6712184355140607
-0.4280933369941015

...

训练好模型之后，用预测程序预测：

predict a1a.t a1a_model_svm a1a_predict_svm（测试样本集文件a1a.t，预测结果保存到a1a_predict_svm文件）

预测结果，预测结果准确率83.8%，可以对比之前RBF核，精度差别不大。

 libsvm和liblinear的比较：

libsvm这个库不支持逻辑斯蒂回归LR，对于SVM，libsvm核liblinear的区别：

libsvm支持非线性核（高斯核、RBF核、多项式核、自定义核、sigmoid核等），这时他得到的模型是非线性模型，可以处理很复杂的非线性的分类问题；liblinear中只有线性核，是线性模型。

libsvm里边的预测函数会统一写成sgn(Σ1~l aiyiK(xi^Txi) + b)（二分类，多分类的实现是通过投票来做的），而在liblinear里边的预测函数是sgn(w^Tx)（w中合并了b）。非线性核运算速度非常慢，如果直接利用libsvm是没办法直接得到w的(线性核可以通过得到的模型计算w，而非线性核无法算w)，而用liblinear可以从模型文件中直接看到w，即liblinear可以直接得到w和b，而libsvm不行。

求解算法不同，libsvm采用的是SMO算法；liblinear采用的是可信域牛顿法（是牛顿法的一个变种，算一个可行域的范围不断地调整它来优化），坐标下降法（每次选出来一个变量进行优化其他变量固定住不动，对于这一个变量的优化一般用牛顿法或者直接求公式解，像是二次函数可以直接求公式解，如果里边带有超越函数如指数函数对数函数那么只能用牛顿法来近似求解它的极值了）。

怎么选择用libsvm还是liblinear呢？如果样本数l比较少及样本的维数n也比较小，可以用libsvm，因为它这时速度不是问题而且精度会更高可以选用RBF核；如果特征向量维数很高即n很大，训练样本数l也很大的话，大到一定程度，没办法选择，在工业应用中只能选择liblinear来解决问题了。

实际应用

[1] Navneet Dalal, Bill Triggs. Histograms of oriented gradients for human detection. computer vision and pattern recognition. 2005.

HOG+L-SVM做行人检测

[2] R. Girshick, J. Donahue, T. Darrell, J. Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2014.

L-SVM做通用目标检测

本集总结：