讲授贝叶斯公式、朴素贝叶斯分类器、正态贝叶斯分类器的原理、实现以及实际应用
大纲：
贝叶斯公式（直接用贝叶斯公式完成分类，计算一个样本的特征向量X属于每个类c的概率，这个计算是通过贝叶斯公式来完成的。）
朴素贝叶斯分类器（预测算法、训练算法）
正态贝叶斯分类器（预测算法、训练算法）
实验环节
实际应用
贝叶斯公式：
澄明了两个相关的（有因果关系的）随机事件以及随机变量之间的概率关系的。
随机事件a、b，假设b是因a是果：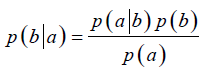
推广到随机变量的情况：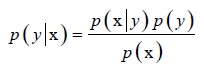
①根据这个公式就可以完成分类了，给定任意一个样本的特征向量X，就可以计算它属于每个类的概率值。
离散的变量p(x)也可推广到连续的情况概率密度函数f(x)，p(x)或f(x)对于每个类yi的概率是相等的一样的，样本属于某个类的概率正比于分子，仅仅以分类为目的而非精确计算样本属于某个类的概率的话，只需计算分子，舍弃分母。
②每个类的条件概率（对连续型随机变量是条件密度函数），统计每个类y它的随机变量x的概率分布就可以了，可以用最大似然估计或其他算法（根据训练样本，把训练样本归类在一起，统计出某个样本的p(x|y)），判定为分子最大的类，即最大化后验概率p(y|x)。
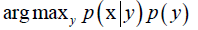
一般情况下，我们是知道每个类y它的样本x所服从的概率分布的p(x|y)（概率密度函数或概率分布表），这称为先验概率，而分类器要做的是反推另一个概率，已知x算它属于某个类的概率，即p(y|x)，刚好和先验概率相反，要得到后验概率的概率。
朴素贝叶斯分类器：简称NB，naive bayes
核心问题是计算p(x|y)*p(y)，p(y)可以简单的设置为每个类出现的概率相等，也可以根据训练样本每个类出现的概率来统计出概率值来。然后核心的问题就是计算所有样本x在每个类下的条件概率p(x|y)（对于连续型变量是条件密度函数，离散型随机变量是条件概率），p(x|y)怎么计算呢？肯定要假设x服从某种概率分布，关键是怎么根据样本估计概率分布（或概率密度函数）中的参数，例如x如果服从正态分布就要估计它的均值和方差（多维是协方差）。有个习惯，现实世界中很多样本就假设它服从正态分布，如人的身高、体重、考试分数等近似服从正态分布，而且中心极限定理也保证了很多随机变量它的极限分布就是一个正态分布。
这里有两种假设：
①第一种就是朴素贝叶斯分类器：假设特征向量x，它的每一个分量相互独立。
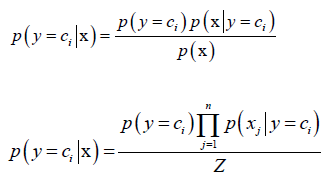
Z是p(x)，归一化因子，对每个类都相等。分子最大化，所属的类ci就是分类的结果。
对于离散型特征：
样本x的分量xi是有限种取值
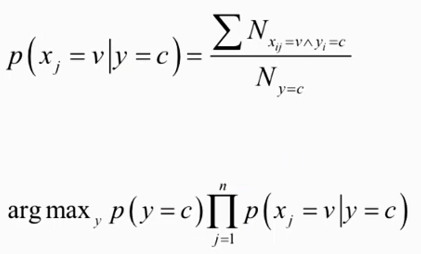
可能所有的样本的某个分量xi都不取某个类c，那么此时p(xj|y=c)的分母就取值为0了，这时对分母都加k（一共k类），分子加1平滑一下，保证概率值加起来等于1。
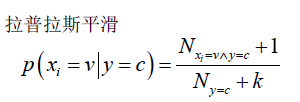
对于连续型特征：
假设x服从一维正态分布。
最大似然固然估计，用样本均值、样本方差来估计正态分布的均值和方差，是有偏估计。
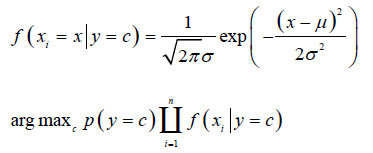
对每个类都要估计，都要算它的均值和方差。
朴素贝叶斯的精髓就是特征向量所有分量之间相互独立，这样就极大地简化问题的求解难度，因为要算一个高维的概率分布是非常麻烦的，但是能把他转化为n个一维的话，情况会简单很多。
正态贝叶斯分类器：简称也是NB，normal bayes
多维
假设样本的特征向量x，对于每个类来说，它的样本特征向量x，服从多维正态分布：
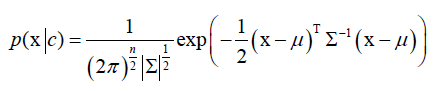，指数里是一个二次型，∑是协方差矩阵，∑-1是它的逆矩阵，|∑|是∑的行列式，和一维正态分布形式上是统一的。
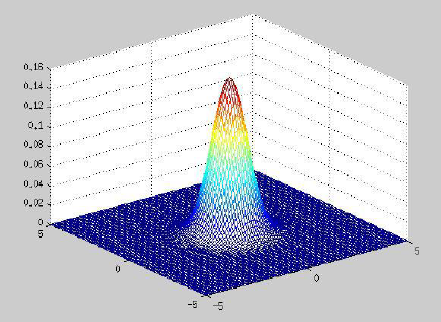
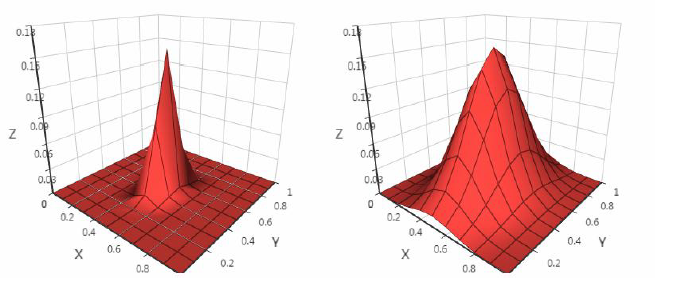
三维以上看不到，均值的地方概率值最大，协方差矩阵决定帽子的宽度、朝向（扁的或圆的）。
假设有一批样本，把样本分成多个类，每个类有一批样本，根据这一批样本用最大似然估计把每个类的均值向量μ和协方差矩阵∑给估计出来，估计出来之后带入贝叶斯判定公式中判定一下就OK了。
训练的时候主要是求解均值向量μ和协方差矩阵∑，在求出μ和∑后，预测的时候稍微麻烦一点：
根据估算出来的协方差矩阵∑求它的逆矩阵∑-1，从而求出p(x|c)。
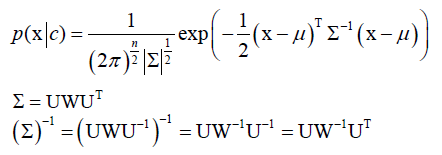
协方差矩阵∑是一个n阶对称方阵，这里求逆矩阵，借助了奇异值分解SVD，对于实对称阵来说，它的奇异值分解就退化为特征值分解了。
对角阵W，正交阵U（UT=U-1）。
|∑|=|U||W||UT|=|W|=∏wii（wii为W对角线元素，因为U是正交阵|U||UT|=1）。
然后将p(x|c)带到贝叶斯分类中，这里假设p(c)是一样的：
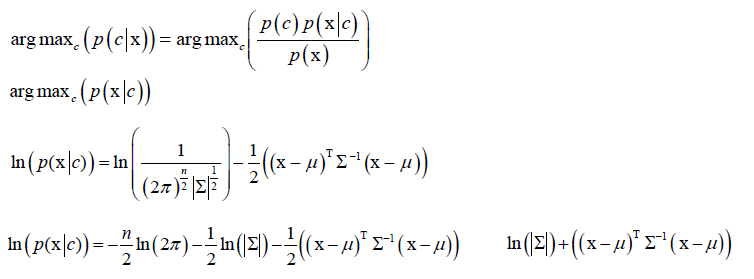
训练的时候每个类都要最大似人估计计算均值向量μ和协方差矩阵∑，在预测的时候只需算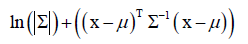
，求它的极小值对应的类即是结果。
实验环节：
贝叶斯分类器是非线性模型，可以解决异或分类问题。
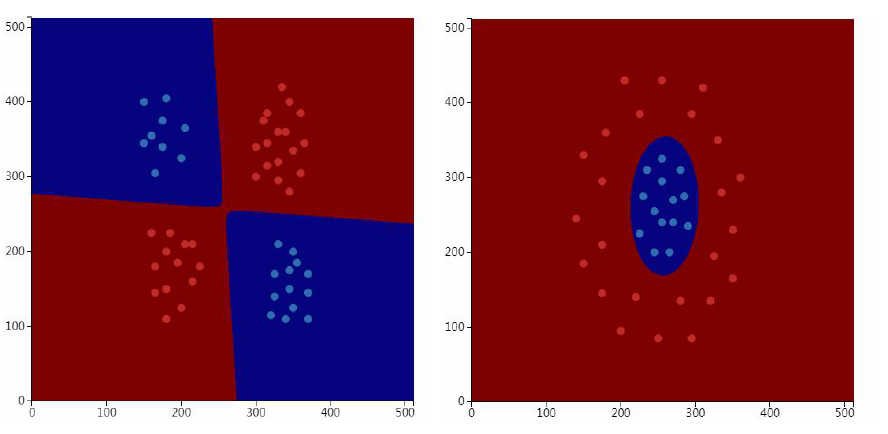
每个类的分布的函数图像的形状不同：
实际应用：
有病没病
垃圾邮件分类问题：根据邮件里边的关键词，来用贝叶斯公式分类，一般用的是朴素贝叶斯，给定指定长度的特征向量，带入到贝叶斯公式中计算。
Mehran Sahami, Susan T Dumais, David Heckerman, Eric Horvitz. A Bayesian Approach to Filtering Junk E-Mail.1998.
文本分类问题：对于文本我们会提一个特征向量出来，一般用tf-idf，它考虑了词频和文档频率的分布。特征向量维度通常非常高，如果要拟合一个高维分布是非常麻烦的，这时可以用朴素贝叶斯。
Yiming Yang, Xin Liu. A re-examination of text categorization methods.international acm sigir conference on research and development in information retrieval, 1999.
智能视频监控中的背景建模算法：摄像机固定不动的时候，人或车在其中走来走去，我们要把这些动的目标抠出来。
Liyuan Li, Weimin Huang, Irene Y H Gu, Qi Tian. Foreground object detection from videos containing complex background. acm multimedia, 2003.
摄像机固定不动，假如1秒学习到40帧图像，学习到背景图像，再来一帧当前最新的图像，来判断每个像素点是前景还是背景，就是二分类问题。选用的特征向量是一点的RGB亮度值和前一帧的差值，把这样一个特征向量带入到贝叶斯公式里去算，算属于前景还是背景的概率，如果前景概率大判断为前景否则为背景，前两个公式带入到第三个全概率公式（每个样本不是属于前景就是属于背景），满足第四个公式则为背景，否则就是前景。关键是怎么得到贝叶斯分类器中的概率分布，通过前面图像的像素点样本的学习得到的。贝叶斯分类器核心是构造特征向量x，训练估计概率分布，预测带入到公式中计算最大值。
人脸识别中的联合贝叶斯模型：把两张照片判定为是否是同一个人，根据姿态、光照因素利用贝叶斯建模。
Dong Chen, Xudong Cao, Liwei Wang, Fang Wen, Jian Sun. Bayesian face revisited: a joint formulation. european conference on computer vision, 2012.
总结：
贝叶斯分类器核心是①构造特征向量x，②训练估计概率分布，③预测带入到公式中计算最大值。