被人牵着鼻子走,到了地方还墨明棋妙地吃一顿砖头。今日头条AI-Lab,其实我一直发现,最擅长的还是点云图像处理,且只是点云处理。
一、C++题目
New 与Malloc的区别:
看这个:New与Malloc区别
虽然malloc()函数的类型是(void *),任何类型的指针都可以转换成(void *),但是最好还是在前面进行强制类型转换,因为这样可以躲过一些编译器的检查。
1) malloc与free是C++/C语言的标准库函数,new/delete是C++的运算符。它们都可用于申请动态内存和释放内存。2) 对于非内部数据类型的对象而言,光用maloc/free无法满足动态对象的要求。对象在创建的同时要自动执行构造函数,对象在消亡之前要自动执行析构函数。由于malloc/free是库函数而不是运算符,不在编译器控制权限之内,不能够把执行构造函数和析构函数的任务强加于malloc/free。因此C++语言需要一个能完成动态内存分配和初始化工作的运算符new,以及一个能完成清理与释放内存工作的运算符delete。注意new/delete不是库函数。我们不要企图用malloc/free来完成动态对象的内存管理,应该用new/delete。由于内部数据类型的“对象”没有构造与析构的过程,对它们而言malloc/free和new/delete是等价的。3) 既然new/delete的功能完全覆盖了malloc/free,为什么C++不把malloc/free淘汰出局呢?这是因为C++程序经常要调用C函数,而C程序只能用malloc/free管理动态内存。如果用free释放“new创建的动态对象”,那么该对象因无法执行析构函数而可能导致程序出错。如果用delete释放“malloc申请的动态内存”,结果也会导致程序出错,但是该程序的可读性很差。所以new/delete必须配对使用,malloc/free也一样。
C++11 的新特性
unique_ptr和shared_ptr的区别:所有权概念。p.671页。对于特定的图像,只能有一个智能指针拥有它,这样只有拥有对象的智能指针的构造函数会删除该对象。然后,让赋值操作转让所有权。这就是用于auto_ptr和unique_ptr的策略,当unique的策略更为严格。
使用引用计数,是shared_ptr采用的策略,仅当最后一个指针过期时,才调用delete。unique能够区分安全和不安全的用法,因为使用了C++11的特性移动构造函数和右值引用功能。
注意:使用new分配内存时,才能使用auto和share,使用new[]分配内存时,不能使用它们。不使用new分配内存时,不能使用auto和share;不使用new或者new[]时,不能使用unique_ptr。
移动语义:移动语义避免了移动原始数据,只是修改了记录。实现方法原理:让编译器知道什么时候需要复制,什么时候不需要复制,这就是右值引用发挥作用的地方。
右值引用:使用移动构造函数。C++.p808.
二、多视几何
极线约束
三、矩阵分析
Cholesky分解和QR分解的区别:建议还是看书,好好把题目再做一遍。
Cholesky分解法又叫平方根法,是求解对称正定线性方程组最常用的方法之一。对于一般矩阵,为了消除LU分解的局限性和误差的过分积累,采用了选主元的方法,但对于对称正定矩阵而言,选主元是不必要的。
Cholesky分解是一种分解矩阵的方法, 在线形代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积(那实数界来类比的话此分解就好像求平方根)。与一般的矩阵分解求解方程的方法比较,Cholesky分解效率很高。
Cholesky分解的条件:
一、Hermitianmatrix:矩阵中的元素共轭对称(复数域的定义,类比于实数对称矩阵)。Hermitiank意味着对于任意向量x和y,(x*)Ay共轭相等
二、Positive-definite:正定(矩阵域,类比于正实数的一种定义)。正定矩阵A意味着,对于任何向量x,(x^T)Ax总是>零(复数域是(x*)Ax>0).
Cholesky分解的形式:
可记作A = L L*。其中L是下三角矩阵。L*是L的共轭转置矩阵。
可以证明,只要A满足以上两个条件,L是唯一确定的,而且L的对角元素肯定是正数。反过来也对,即存在L把A分解的话,A满足以上两个条件。
如果A是半正定的(semi-definite),也可以分解,不过这时候L就不唯一了。
特别的,如果A是实数对称矩阵,那么L的元素肯定也是实数。
另外,满足以上两个条件意味着A矩阵的特征值都为正实数,因为Ax = lamda * x,(x*)Ax = lamda * (x*)x > 0, lamda > 0.
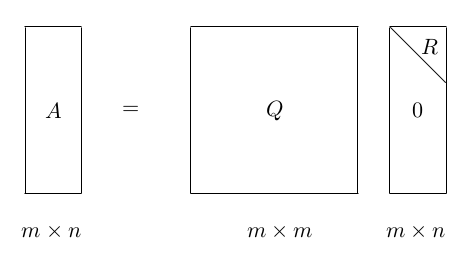
-QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。用一张图可以形象地表示QR分解:
这其中, Q为正交矩阵,QTQ=I,R为上三角矩阵。
实际中,QR分解经常被用来解线性最小二乘问题。
Cholesky分解只能用于正定对称矩阵,但实际方程组中,正定对称矩阵不一定满足,在接近正定的矩阵时,会产生病态矩阵问题。QR是一种泛用的方法。
常见的矩阵分解有可逆方阵的三角(LU)分解、任意满秩矩阵的正交三角(QR)分解、对称正定矩阵的Cholesky分解,以及任意方阵的Schur分解、Hessenberg分解、EVD分解、SVD分解、GMD分解等。
(1)可逆方阵的LU分解
矩阵的LU分解就是将一个矩阵表示为一个交换下三角矩阵和一个上三角矩阵的乘积形式。线性代数中已经证明,只要方阵A是非奇异的(即可逆的),LU分解总是可以进行的。
当L为单位下三角矩阵而U为上三角矩阵时,此三角分解称为杜利特(Doolittle)分解。当L为下三角矩阵而U为单位上三角矩阵时,此三角分解称为克劳特(Crout)分解。显然,如果存在,矩阵的三角分解不是唯一的。
(PS:方阵A可唯一地分解为A=LDU(其中L,U分别为单位下,上三角矩阵,D为对角矩阵)的充分必要条件为A的前n-1个顺序主子式都不为0。特别:对n阶对称正定矩阵,存在一个非奇异下三角矩阵L,使得A=LL'成立。)
MATLAB提供的lu函数用于对矩阵进行LU分解,其调用格式为:
[L,U] =lu(X):产生一个上三角阵U和一个变换形式的下三角阵L(行交换),使之满足X=LU。注意,这里的矩阵X必须是方阵。
[L,U,P]=lu(X):产生一个上三角阵U和一个下三角阵L以及一个置换矩阵P,使之满足PX=LU。当然矩阵X同样必须是方阵。
(2) 满秩矩阵的QR分解
对矩阵X进行QR分解,就是把X分解为一个正交矩阵Q和一个上三角矩阵R的乘积形式。QR分解只能对方阵进行。MATLAB的函数qr可用于对矩阵进行QR分解,其调用格式为:
[Q,R] =qr(X): 产生一个一个正交矩阵Q和一个上三角矩阵R,使之满足X=QR。
[Q,R,E]=qr(X):产生一个一个正交矩阵Q、一个上三角矩阵R以及一个置换矩阵E,使之满足XE=QR。
(3)对称正定矩阵的Cholesky分解
如果矩阵X是对称正定的,则Cholesky分解将矩阵X分解成一个下三角矩阵和上三角矩阵的乘积。设上三角矩阵为R,则下三角矩阵为其转置,即X=R'R。MATLAB函数chol(X)用于对矩阵X进行Cholesky分解,其调用格式为:
R =chol(X):产生一个上三角阵R,使R'R=X。若X为非对称正定,则输出一个出错信息。
[R,p]=chol(X):这个命令格式将不输出出错信息。当X为对称正定的,则p=0,R与上述格式得到的结果相同;否则p为一个正整数。如果X为满秩矩阵,则R为一个阶数为q=p-1的上三角阵,且满足R'R=X(1:q,1:q)。
(4)任意方阵的Schur分解
任意一个n阶方阵X可以分解为X=URU',其中U为酉矩阵,R为上三角schur矩阵且其主对角线上的元素为X的特征值。
[U,R]=schur(X)
(5)任意方阵的Hessenberg分解
任意一个n阶方阵X可以分解为X=PHP', 其中P为酉矩阵, H的第一子对角线下的元素均为0,即H为Hessenberg矩阵。
[P,H]=hess(X)
(6)任意方阵的特征值分解EVD
任意一个n阶方阵X可以分解为XV=VD,其中D为X的特征值对角阵,V为X的特征向量矩阵。
[V,D]=eig(X)
[V,D]=eig(X,Y)计算广义特征值矩阵D和广义特征值向量矩阵V,使得XV=YVD。
(7)任意矩阵的奇异值分解SVD
任意一个m*n维的矩阵X可以分解为X=USV',U,V均为酉矩阵,S为m*n维的对角矩阵,其对角线元素为X的从大到小排序的非负奇异值。
[U,S,V]=svd(X)
(8) 任意矩阵的几何均值分解GMD
任意矩阵m*n维的矩阵X可以分解为X=QRP', Q,P均为酉矩阵,R为k*k维的实正线上三角矩阵,其主对角线元素均等于X的所有K个正奇异值的几何均值,k=rank(X)。
(PS: 一个n × n的实对称矩阵 M 是正定的当且仅当对于所有的非零实系数向量z,都有 zTMz > 0。其中zT 表示z的转置。
对于复数的情况,定义则为:一个n × n的埃尔米特矩阵 M 是正定的当且仅当对于每个非零的复向量z,都有z*Mz > 0。其中z* 表示z的共轭转置。由于 M是埃尔米特矩阵,经计算可知,对于任意的复向量z,z*Mz必然是实数,从而可以与0比较大小。因此这个定义是自洽的。正定方阵M的所有的特征值 λi都是正的。)
四、编程题目
广度优先遍历--使用队列;
使用一个先进先出的队列,可以实现一个二叉树的广度优先遍历BFS。
五、深度图像
面元提取、三维特征、