Xenon's Attack on the Gangs，题解

题目：

　　

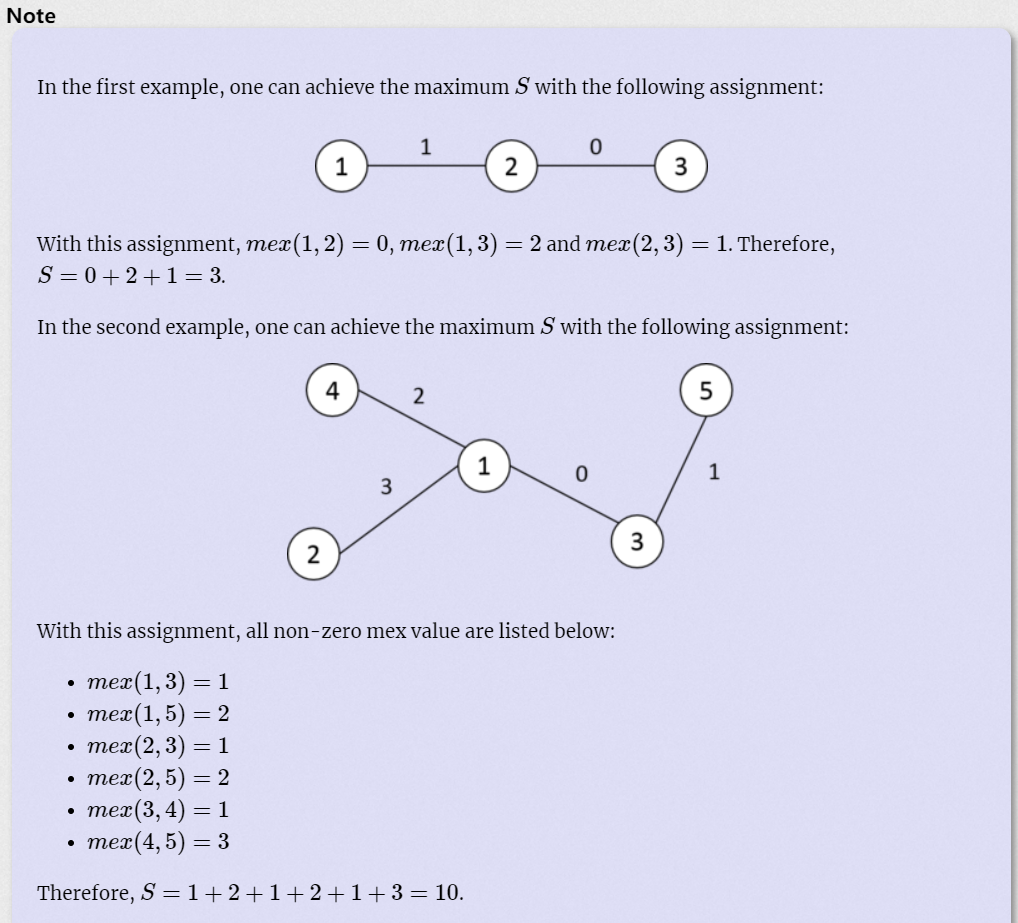
题意：

　　有一个n个节点的树，边权为0-n-2，定义mex（a，b）表示除了ab路径上的自然数以外的最小的自然数，求如何分配边权使得所有的mex（a，b）之和最大。

分析：

　　看似有点乱，我们先不急着出答案，先想想这个式子，我们要求mex的和怎么办呢？我们想一想这个：一大堆节点-----一大堆节点（中间是个边权为0的边），于是，同一堆中节点节点无论从谁到谁，都逃不掉为0的命运，谁让它里面没有0呢，而如果从第一堆到第二堆（或从第二堆到第一堆，其实是一样的），那么他们的mex知少是1，因为除了0最小的自然数就是1了。好的，那么它至少为左边的节点的个数*右边的节点的个数。于是呢？我们再来想一想还有什么性质，经过深思熟虑，我们发现，如果0的左右节点都没有1，我们把1和某个节点换过来，它将会更优，为什么呢，首先，不过0的路径肯定mex=0，而过0的如果有过1和这个节点，交换之后它不变（因为过的节点都没变），如果过0和这个节点且不过1，那么他原来就是1，而换完之后便至少是2，如果原来过0和1，这个可以不用考虑，为什么呢：如果着个0和1已经相邻了，肯定不与要证命题想背，如果不临着，我就换成这个路径上临着的就完了，于是，我们有0有临必有1（这里的必指的是不会更差），同样的，我们可以证明如果路径a-b有n条边，且权值是0-n-1，则有临必（同上）有n。于是，我们知道了，这颗树满足性质A：0连接两点满足A，有0边权的边相连的两个节点存在两个在不同节点上的方向走到度为1的节点（当然，本身度为1也算），使得这些路径上的权值是从0开始连续的，并且去掉其中较大的度为1的节点仍满足性质A（注意是递归定义，不是去掉一次就算了）。这句话。。。我不知道我为啥要用这么长的一句话表述，不过我觉的我这句话还算比较明白的。

　　换一行，要不大家看不下去就麻烦了。。。

　　证明这个之后呢？没错我们要枚举让没两个度为1的节点都尝试做这两个节点，可是这怎么枚举呢，当然我们还要关注“主链”旁边的“支链”。我们想一下递归/推关系吧，我们定义fab表示a到b这条链为从0开始的链序自然数的序列至少会获得的价值（如果是两个度为1的节点，就是将会获得的价值），定义ffab表示a向b方向走一边所到的节点，fffab表示ab这条链必须经过a才能到达b的节点的个数。于是，fab=max（f（ffab）bf，fa（ffba））+fffab*fffba。这是啥。。。这个要怎么解释。。。用文字的话这个可能说的非常的数学化，大家可能不太喜欢，我就用朴实一点的语言描述一下（当然喜欢数学化语言的就去读一下第一段的部分内容吧），他是这样的fab其实就是链的左边是最大的还是列的右边是最大（此节点的权值为n）的，然后两边的节点由原来的至少n变为至少n+1于是都加上1就好了，于是式子出来了。

　　式子出来了，可是这个可以递推吗，其实这个没有必要（当然也应该算是可以，只是不占优势，直接递归就好了），我们直接用数组记录，然后每个值只会算到1次，于是就不会超时了。然后就是ffab和fffab怎么求出来呢？Dfs，n次dfs，ffab其实就是b为根a的父亲，fffab就是b为根时a的儿子节点，但是，有人说：可以二次元换根吗？这个问题。。。要处理的数据就是n*n个，怎么说你都要处理出来，就是n*n的复杂度，不换就好了，当然应该是可以换，就是处理麻烦一点（其实还是要赋原来的值）。

　　最后答案是什么呢，其实就是max（fab），那这不会出现最大的fab中a，b不是度为1的节点吗？看转移方程，不会吧。

　　long long用不用呢，这个应该是取决于一条3000的一条链的答案，可以自己跑一下试试，当然多用一些问题也不大。

　　好的，基本就这些，然后是代码。

#include <cstdio>
#include <string>
using namespace std;
const int maxn=3000+10;
struct E{
    int to;
    int next;
    E(){
        to=next=0;
    }
}ed[maxn*2];
int head[maxn];
int tot;
void J(int a,int b){
    tot++;
    ed[tot].to=b;
    ed[tot].next=head[a];
    head[a]=tot;
}
int son[maxn][maxn];//这里定义有点不同，大家应该可以理解
int P[maxn][maxn];
long long f[maxn][maxn];
void Dfs(int root,int x,int fa){
    P[root][x]=fa;
    son[root][x]=1;
    for(int i=head[x];i;i=ed[i].next){
        if(ed[i].to==fa)
            continue;
        Dfs(root,ed[i].to,x);
        son[root][x]+=son[root][ed[i].to];
    }
}
long long Cl(int a,int b){//递归
    if(a==b)
        return 0;
    if(f[a][b])
        return f[a][b];
    return f[a][b]=max(Cl(P[b][a],b),Cl(P[a][b],a))+(long long)son[b][a]*(long long)son[a][b];//勤用long long少出错
}
int main(){
    int n;
    scanf("%d",&n);
    int js1,js2;
    for(int i=1;i<=n-1;i++){
        scanf("%d%d",&js1,&js2);
        J(js1,js2);
        J(js2,js1);
    }
    for(int i=1;i<=n;i++)//处理一些信息
        Dfs(i,i,0);
    long long ans=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            ans=max(ans,Cl(i,j));
    printf("%lld",ans);
    return 0;
}