1.神经元模型
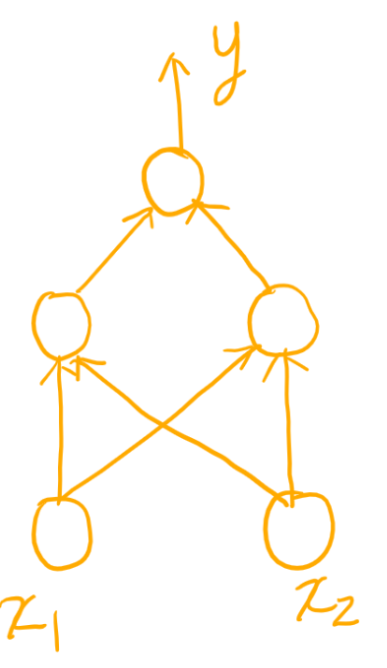
神经网络能模拟生物神经系统对真实世界的反应,最基本的成分时神经元模型,如图。
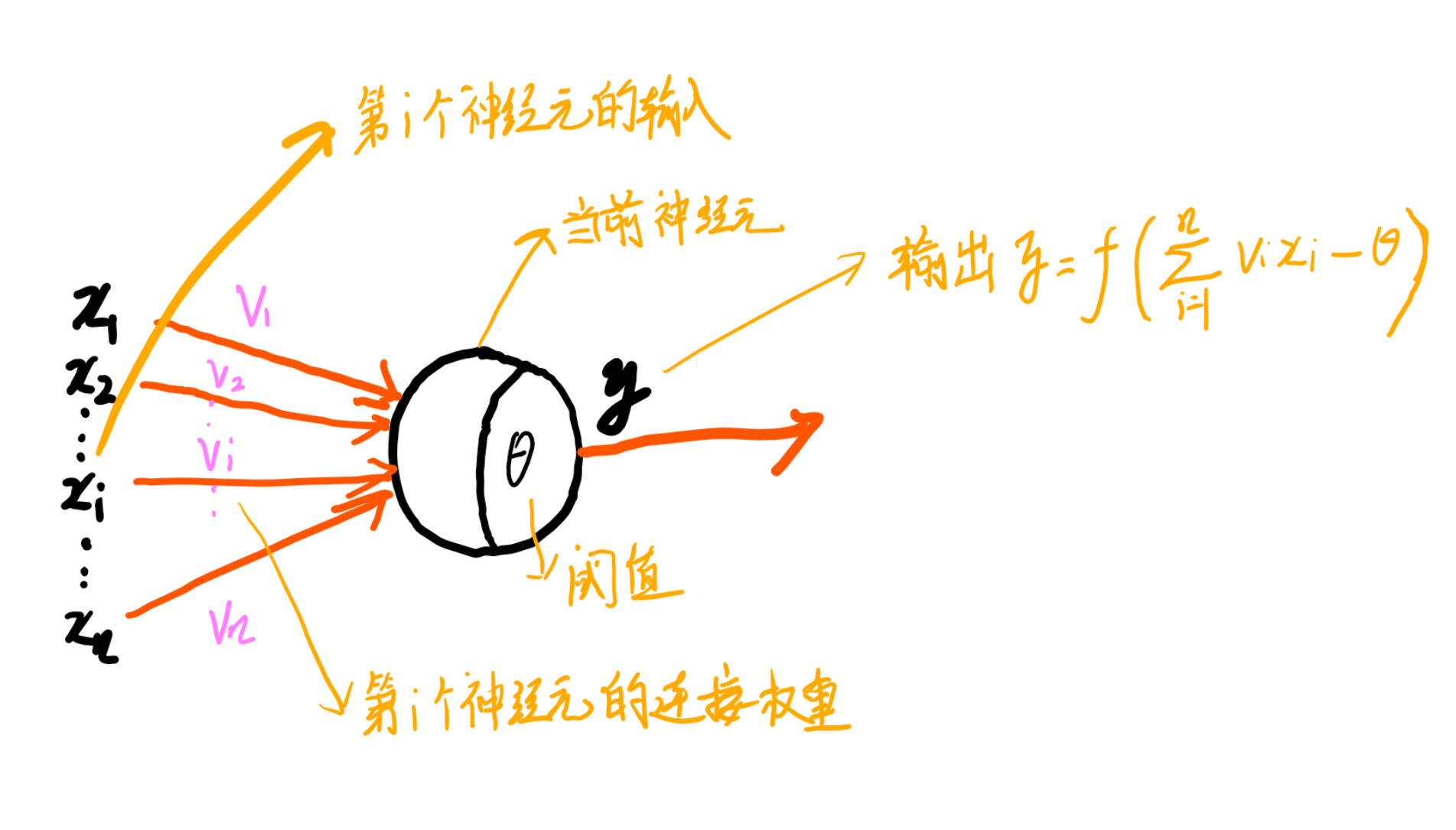
神经元接收来自其他n个神经元的输入,通过带权重的连接传入,将接收到的总输入与阈值比较,然后通过激活函数处理产生输出。
理想激活函数是阶跃函数,将输入映射为输出值0和1。1对应于神经元兴奋,0对应不兴奋。
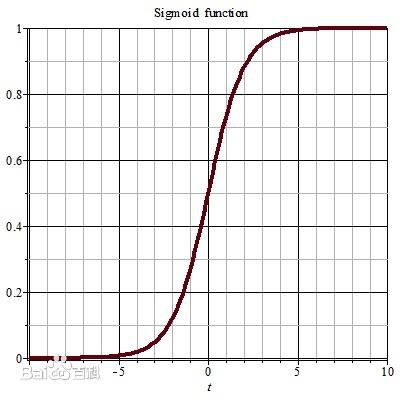
由于阶跃函数不连续、不光滑,实际常用sigmoid函数,sigmoid将输入值挤压在(0,1)范围内。
2.多层前馈神经网络
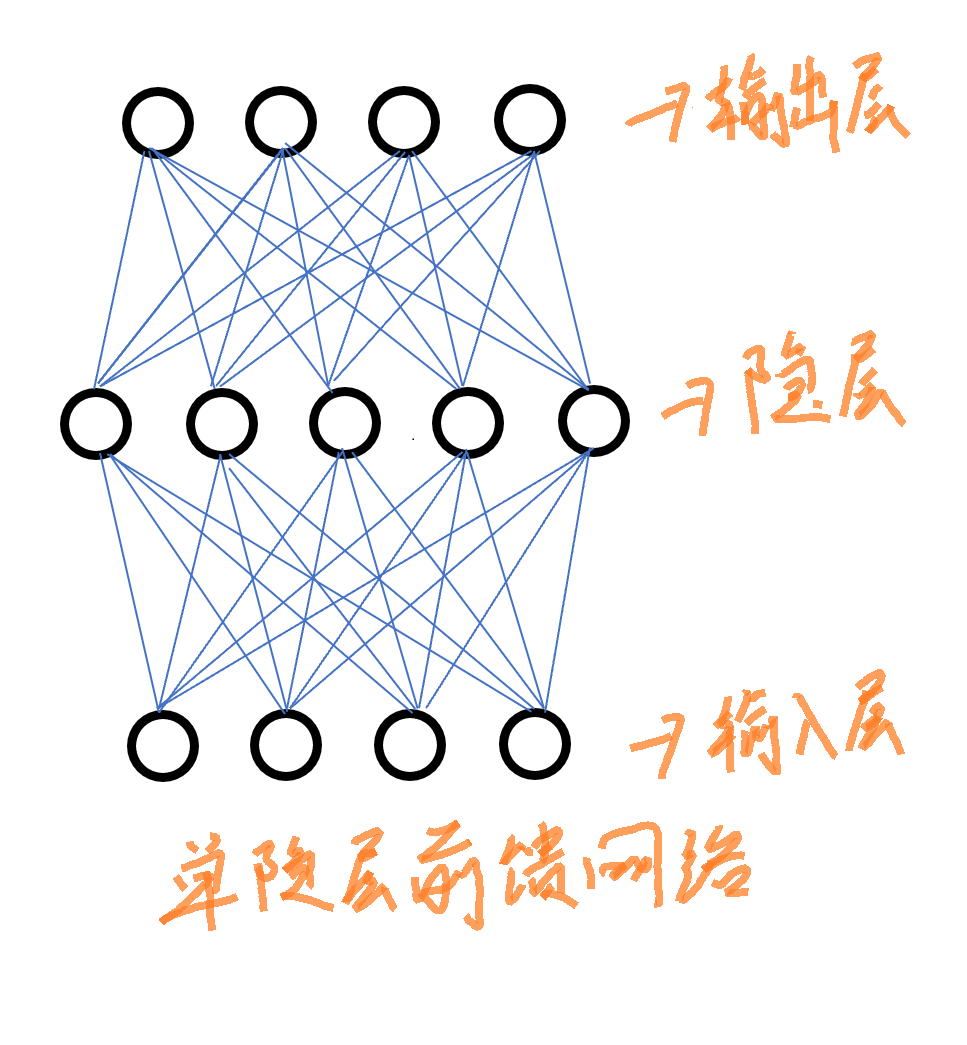
多层前馈神经网络,每层神经元与下一层神经元互联,不存在同层连接和跨层连接。
输入层神经元接收外界输入,隐层与输出层进行处理,最后由输出层输出。
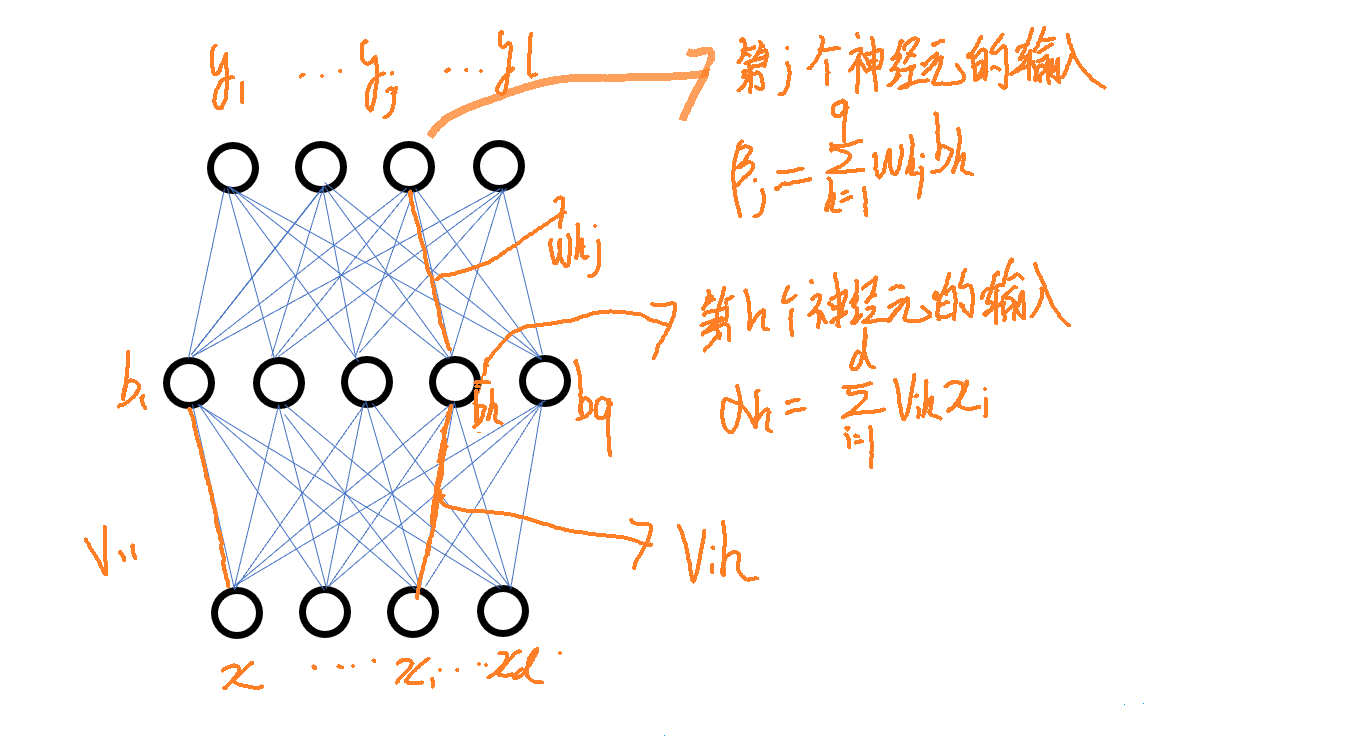
3.误差逆传播算法
要训练神经网络,可以使用误差逆传播(BP)算法。

4.例子
用神经网络实现异或运算
代码
1 import numpy as np 2 3 #sigmoid函数 4 def sigmoid1(x): 5 a=1/(1+np.exp(-x)) 6 return a 7 8 #训练集 9 xunlianji=np.array([[1,1,0],[1,0,1],[0,1,1],[0,0,0]]) 10 yy=np.zeros((4,1)) 11 eta=0.1 12 #定义连接权、阈值 13 vih=np.random.rand(2,2) #输入层与隐层连接权 14 delt_vih=np.zeros((2,2)) 15 r=np.random.rand(1,2) #隐层阈值 16 delt_r=np.zeros((1,2)) 17 whj=np.random.rand(2,1) #隐层与输出层连接权 18 delt_whj=np.zeros((2,1)) 19 o=np.random.rand(1,1) #输出层阈值 20 delt_o=np.zeros((1,1)) 21 #创建隐层 22 alph=np.zeros((1,2)) 23 b=np.zeros((1,2)) 24 e=np.zeros((1,2)) #隐层梯度项 25 #创建输出层 26 beita=np.zeros((1,1)) 27 y=np.zeros((1,1)) 28 g=np.zeros((1,1)) #输出层梯度项 29 #主循环 30 for daishu in range(0,1000000): 31 for xunlian in range(0,4): 32 #计算隐层的输入 33 alph[0,0]=vih[0,0]*xunlianji[xunlian,0]+vih[1,0]*xunlianji[xunlian,1] 34 alph[0,1]=vih[0,1]*xunlianji[xunlian,0]+vih[1,1]*xunlianji[xunlian,1] 35 #计算隐层输出 36 b[0,0]=sigmoid1(alph[0,0]-r[0,0]) 37 b[0,1]=sigmoid1(alph[0,1]-r[0,1]) 38 #计算输出层的输入 39 beita[0,0]=whj[0,0]*b[0,0]+whj[1,0]*b[0,1] 40 #输出层输出 41 y[0,0]=sigmoid1(beita[0,0]-o[0,0]) 42 yy[xunlian,0]=y[0,0] 43 #输出层梯度项 44 g[0,0]=y[0,0]*(1-y[0,0])*(xunlianji[xunlian,2]-y[0,0]) 45 #隐层梯度项 46 e[0,0]=b[0,0]*(1-b[0,0])*(whj[0,0]*g[0,0]) 47 e[0,1]=b[0,1]*(1-b[0,1])*(whj[1,0]*g[0,0]) 48 #更新连接权和阈值 49 delt_whj[0,0]=eta*g[0,0]*b[0,0] 50 delt_whj[1,0]=eta*g[0,0]*b[0,1] 51 whj[0,0]=delt_whj[0,0]+whj[0,0] 52 whj[1,0]=delt_whj[1,0]+whj[1,0] 53 delt_o[0,0]=-(eta*g[0,0]) 54 o[0,0]=delt_o[0,0]+o[0,0] 55 delt_vih[0,0]=eta*e[0,0]*xunlianji[xunlian,0] 56 delt_vih[1,0]=eta*e[0,0]*xunlianji[xunlian,1] 57 delt_vih[0,1]=eta*e[0,1]*xunlianji[xunlian,0] 58 delt_vih[1,1]=eta*e[0,1]*xunlianji[xunlian,1] 59 vih[0,0]=vih[0,0]+delt_vih[0,0] 60 vih[1,0]=vih[1,0]+delt_vih[1,0] 61 vih[0,1]=vih[0,1]+delt_vih[0,1] 62 vih[1,1]=vih[1,1]+delt_vih[1,1] 63 delt_r[0,0]=-(eta*e[0,0]) 64 delt_r[0,1]=-(eta*e[0,1]) 65 r[0,0]=delt_r[0,0]+r[0,0] 66 r[0,1]=delt_r[0,1]+r[0,1] 67 xunlianji=xunlianji.astype(np.float64) 68 xunlianji[:,2]=yy[:,0] 69 print(xunlianji)
结果
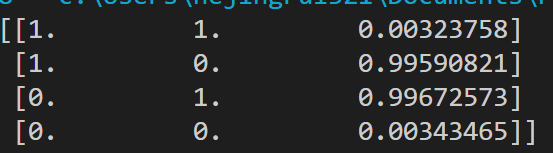
可以发现训练结果越来越接近0 1 1 0.