为什么要梯度下降,因为在机器学习与视觉SLAM中,有关目标函数的最优值求解过程,都会涉及到目标函数求解,这个过程需要梯度下降。今天我们从最简单,最古老,最经典的最小二乘开始。本文以线性最小二乘为例子,至于非线性最小二乘问题,其中增量方程的求解算法很多,以后再更新。


下面我们借助 opencv, 将 最小二乘算法应用于直线拟合。
1 #define _CRT_SECURE_NO_WARNINGS 2 #include<vector> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 #include<opencv2/opencv.hpp> 8 using namespace cv; 9 10 // 功能:打印数组 11 void printVec(vector<double>& vec) 12 { 13 for (auto& ele:vec) 14 { 15 cout << ele << " "; 16 } 17 cout << endl; 18 } 19 20 // 功能:打印Mat 21 void printMat(Mat& mat) 22 { 23 for (int j = 0; j < mat.rows; j++) 24 { 25 for (int i = 0; i < mat.cols; i++) 26 { 27 cout.width(10); 28 if (abs(mat.ptr<double>(j)[i]) < 1e-5) 29 { 30 cout << "0"; 31 } 32 else 33 { 34 cout << mat.ptr<double>(j)[i]; 35 } 36 } 37 cout << endl; 38 } 39 cout << endl; 40 } 41 42 // 功能: 计算误差平方和 43 double SSE(vector<double> x, vector<double> y , Mat ANSS) 44 { 45 double errors = 0; 46 for (size_t i = 0; i < y.size(); i++) // 0 47 { 48 double y_predict = 0; 49 for (size_t j = ANSS.rows; j > 0; j--) // 0 50 { 51 y_predict += ANSS.ptr<double>(ANSS.rows - j)[0]*pow(x[i], j - 1); 52 } 53 errors += pow(y[i] - y_predict, 2); 54 } 55 return errors; 56 } 57 int main() 58 { 59 fstream f("least_square.txt", ios::out); 60 vector<double> x{ 2,4,5,6,6.8,7.5,9,12,13.3,15}; 61 vector<double> y{ -10,-6.9,-4.2,-2,0,2.1,3,5.2,6.4,4.5 }; 62 //<1>写入 x、y 63 for (auto& ele : x) 64 { 65 f << ele << " "; 66 } 67 f << endl; 68 for (auto& ele : y) 69 { 70 f << ele << " "; 71 } 72 f << endl; 73 74 int k = x.size(); 75 for (int n = 1; n <= 10; n++) 76 { 77 //int n = 1; 78 Mat X0 = Mat::zeros(k, n + 1, CV_64F); // 这里需要注意 CV_64F <-- double 79 X0 = X0.t(); 80 //<2>构建矩阵x0 81 for (int j = 0; j <= X0.rows - 1; j++) // [0, 1] 82 { 83 for (int i = 0; i <= X0.cols - 1; i++)//[0, 9] 84 { 85 X0.ptr<double>(j)[i] = pow(x[i], X0.rows - j - 1); 86 } 87 } 88 Mat ANSS = Mat::zeros(n + 1, 1, CV_64F); 89 Mat y_ = Mat::zeros(y.size(), 1, CV_64F); 90 for (int i = 0; i < y.size(); i++) 91 { 92 y_.ptr<double>(i)[0] = y[i]; 93 } 94 ANSS = (X0*X0.t()).inv()*X0*y_; 95 printMat(ANSS); 96 cout << "SSE = " << SSE(x, y, ANSS) << endl; 97 // < >写入拟合参数 98 for (int j = 0; j < ANSS.rows; j++) 99 { 100 f << ANSS.ptr<double>(j)[0] << " "; 101 } 102 f << endl; 103 cout << "----------" << endl; 104 } 105 return 0; 106 }

看到上述代码计算出来 4次拟合结果和matlab拟合工具箱计算结果基本一致,OK,再看 10 次拟合 的最小误差平方和是最小的,一般次数过高导致过拟合。
【后续增加置信度等等拟合结果评价参数】 
现在我们在Matlab键入如下数据并拟合
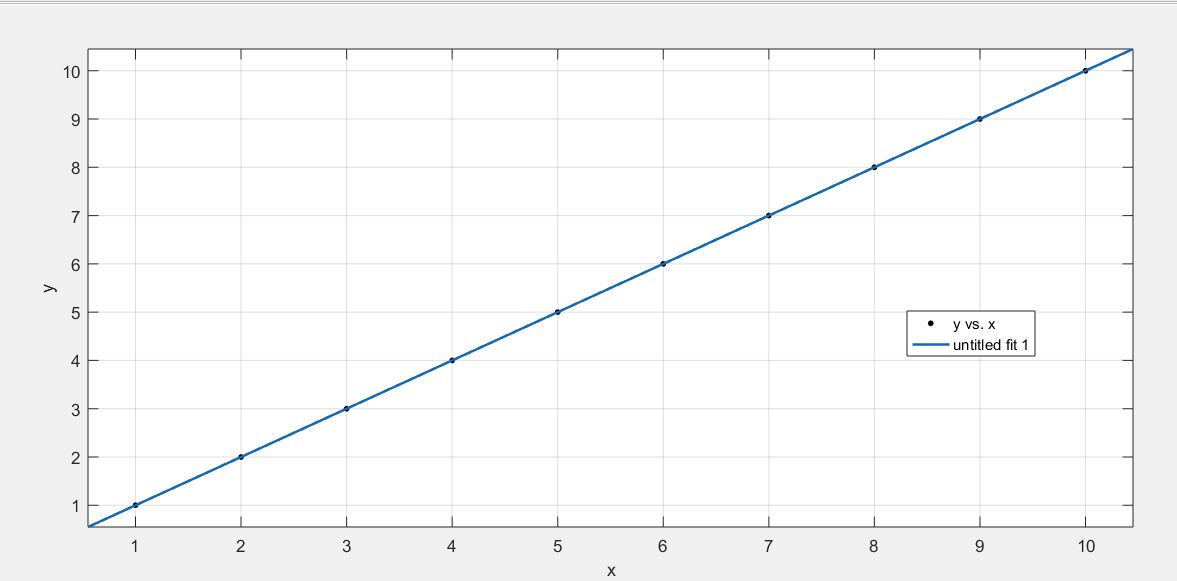
x = 1:1:10;
y = 1:1:10;
我们用拟合工具箱,一次拟合如下图:
现在假设x = 11的时候,传感器故障了,采回的数据出现错误,y = 100;此时,我们还用上面拟合工具箱进行拟合,得出效果如下:
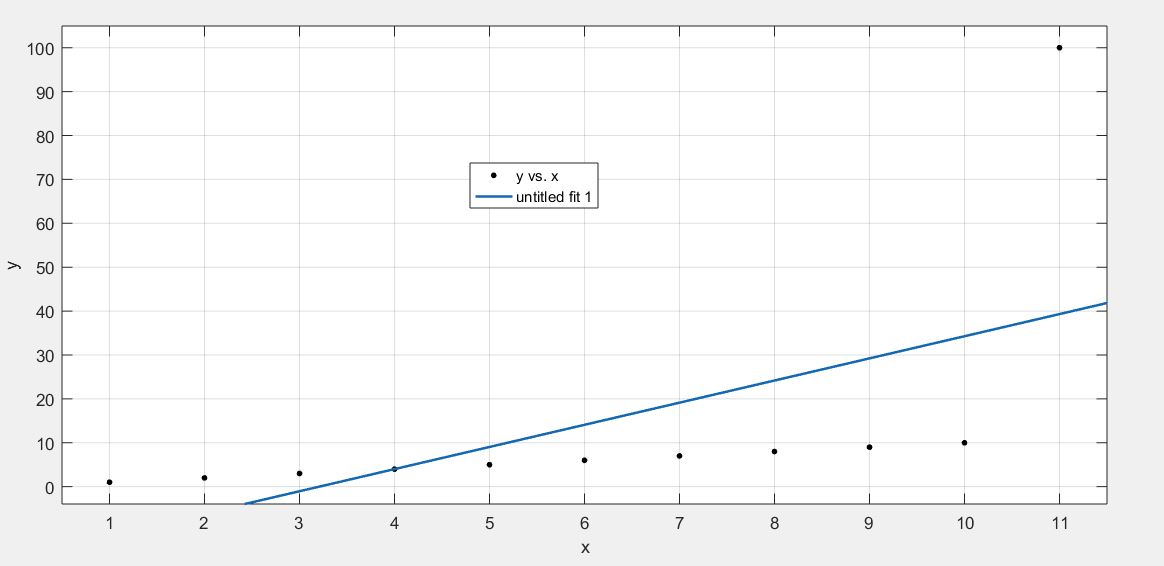
显然,拟合效果非常差,因为最小二乘将错误的样本数据对参数的估计也引入了;此时,这种方法失效,我们下一节介绍Ransac算法来进行改进“最小二乘的抗噪性”不足这一缺点。
参考:https://blog.csdn.net/StupidAutofan/article/details/78924601