
其中排列组合公式如图:
![]()
python实现代码如下:
1 import operator 2 3 # Cnk = [ n (n-1)(n-2)....(n-k+1) ] / k的阶乘 4 def c(n, k): 5 # reduce 用法 https://www.liaoxuefeng.com/wiki/897692888725344/989703124920288 6 # 参数mul表示multiply,表示连乘 7 return reduce(operator.mul, range(n-k+1, n+1)) / reduce(operator.mul, range(1, k+1)) 8 9 #有重复的重采样 10 def bagging(n, p): 11 s = 0 12 #如果9个人投票,56789都是对的,所以从 n/2+1开始 13 for i in range(n / 2 + 1, n + 1): 14 #二项分布啦 15 s += c(n, i) * p ** i * (1 - p) ** (n - i) 16 return s 17 18 19 if __name__ == "__main__": 20 for t in range(10, 101, 10): 21 ## 0.6表示一个分类器的准确率; t表示若干次采样 22 print t, '次采样正确率:', bagging(t, 0.6)
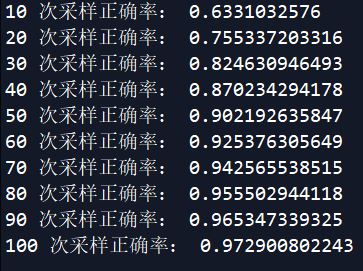
在上述公式中用,如果 a = 0.6,则b = 0.4,那么当n越大,和的结果越趋近于1。
c++实现代码:
由于阶乘有连续乘法,容易溢出,以下代码没有作过多溢出处理。也可以在公式上优化“排列组合”的计算方式来防止溢出
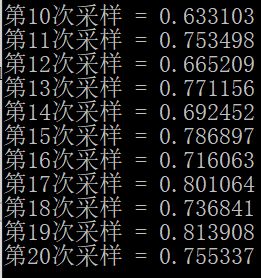
1 #include<iostream> 2 #include<math.h> 3 #include<vector> 4 using namespace std; 5 // 连乘 6 long long Multiplicative(int lower, int higher) 7 { 8 if (higher < lower) 9 { 10 return -1; 11 } 12 long long ret = 1; 13 for (; lower <= higher; lower++) 14 { 15 ret *= lower; 16 } 17 return ret; 18 } 19 // 排列组合Cnk 20 // Cnk = [n(n - 1)(n - 2)....(n - k + 1)] / k的阶乘 21 int PermutationAndCombination(int n, int k) 22 { 23 //cout << Multiplicative(n - k + 1, n) << ";" << Multiplicative(1, k) << endl; 24 return Multiplicative(n-k+1, n)/Multiplicative(1, k); 25 } 26 27 // 有重复的采样 28 float Bagging(int n, float p) 29 { 30 float s = 0.0; 31 for (int i = n / 2 + 1; i < n + 1; i++) 32 { 33 s += PermutationAndCombination(n, i)*pow(p, i)*pow(1 - p, n - i); 34 } 35 return s; 36 } 37 38 int main() 39 { 40 // 累乘测试 41 cout << Multiplicative(2, 4) << endl; 42 // 排列组合测试 43 cout << PermutationAndCombination(4, 2) << endl; 44 cout << PermutationAndCombination(10, 3) << endl; 45 cout << PermutationAndCombination(30, 2) << endl; 46 vector<int> vec; 47 for (int i = 10; i < 21; i++) 48 { 49 cout << "第" << i << "次采样 = " <<Bagging(i, 0.6) << endl; 50 } 51 return 1; 52 }
有关SVD分解,参考我之前一篇博客《特征/SVD分解(图像压缩)/PCA降维简介》,这里仅给出python代码。
链接:https://www.cnblogs.com/winslam/p/9971732.html
1 import numpy as np 2 import os 3 import cv2 4 import matplotlib.pyplot as plt 5 import matplotlib as mpl 6 from pprint import pprint 7 8 # SVD分解的逆运算 9 def restore1(sigma, u, v, K): # 奇异值、左特征向量、右特征向量 10 m = len(u) 11 n = len(v[0]) 12 a = np.zeros((m,n)) 13 for k in range(K): 14 uk = u[:,k].reshape(m, 1) 15 vk = v[k].reshape(1,n) 16 a += sigma[k] * np.dot(uk, vk) 17 a[a < 0] = 0 18 a[a > 255] = 255 19 # a = a.clip(0, 255) 20 #四舍五入取整数 21 return np.rint(a).astype('uint8') 22 23 if __name__ == "__main__": 24 A = cv2.imread("6.son.png", -1) 25 a = np.array(A) 26 K = 50 27 u_r, sigma_r, v_r = np.linalg.svd(a[:,:,0]) 28 u_g, sigma_g, v_g = np.linalg.svd(a[:,:,1]) 29 u_b, sigma_b, v_b = np.linalg.svd(a[:,:,2]) 30 #R = restore1(sigma_r, u_r, v_r, 5) 31 for k in range(1, K+1): 32 R = restore1(sigma_r, u_r, v_r, k) 33 G = restore1(sigma_g, u_g, v_g, k) 34 B = restore1(sigma_b, u_b, v_b, k) 35 # 参考 https://blog.csdn.net/wgx571859177/article/details/80987459 36 I = np.stack((R,G,B), 2) 37 cv2.imshow('image', I) 38 cv2.waitKey(100) 39 #这一句还是要加上 40 cv2.destroyAllWindows()