【题解】 AT2134 Zigzag MST

【题解】AT2134 Zigzag MST

一道MST好题

$Anson$有云：

• 要么是减少边的数量。
• 要么是改变连接边的方式。

那么如何减少边的数量呢？很简单，把所有不可能对答案产生贡献的边去掉也就是不加，这样就可以减少边的数量了。

怎么改变边的连接方式？很简单，考虑这样子的情况$ (1->2),(2->3)(。此时我们连接一个)(1->3)$就好了，类比向量？，确实。

那么这一题怎么考虑呢？？

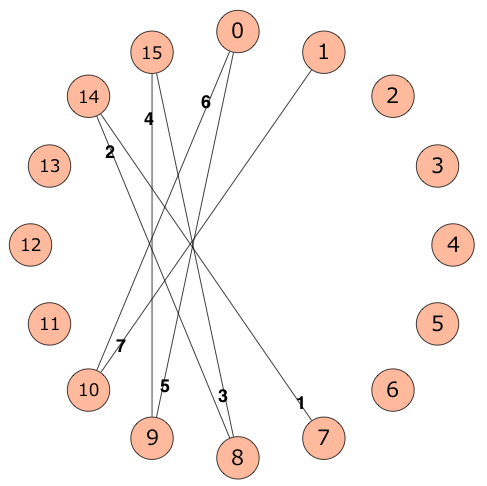
发现没有，$(7->14)(和)(14->8)(有一组边，我们直接可以连接)(7->8)$,就变成递推了。

设置$f(x)$是编号$x$点从逆时针方向走过来的最短距离。

考虑初始条件，对于三元组$(a,b,c) , f(a)=c+1,f(b)=c+2$，这样子这只初始条件到时候就只要递推就好了，转移就是$f(x)=f(x-1)+2 , x$在$mod n$下。取Min就好了

#include<bits/stdc++.h>
#define int ll
using namespace std;typedef long long ll;
#define DRP(t,a,b) for(register int t=(a),edd=(b);t>=edd;--t)
#define RP(t,a,b)  for(register int t=(a),edd=(b);t<=edd;++t)
#define ERP(t,a)   for(register int t=head[a];t;t=e[t].nx)
#define midd register int mid=(l+r)>>1
#define TMP template < class ccf >
#define lef l,mid,pos<<1
#define rgt mid+1,r,pos<<1|1
#define pushup(pos) (seg[pos]=seg[pos<<1]+seg[pos<<1|1])
TMP inline ccf qr(ccf b){
    register char c=getchar();register int q=1;register ccf x=0;
    while(c<48||c>57)q=c==45?-1:q,c=getchar();
    while(c>=48&&c<=57)x=x*10+c-48,c=getchar();
    return q==-1?-x:x;}
TMP inline ccf Max(ccf a,ccf b){return a<b?b:a;}
TMP inline ccf Min(ccf a,ccf b){return a<b?a:b;}
TMP inline ccf Max(ccf a,ccf b,ccf c){return Max(a,Max(b,c));}
TMP inline ccf Min(ccf a,ccf b,ccf c){return Min(a,Min(b,c));}
TMP inline ccf READ(ccf* _arr,int _n){RP(t,1,_n)_arr[t]=qr((ccf)1);}
//----------------------template&IO---------------------------
const int maxn=200005;
struct E{
    int fr,to,w;
    inline bool operator < (E a){return w<a.w;}
}e[maxn<<1];
int cnt;
int r[maxn];
inline void add(int fr,int to,int w){
    e[++cnt]=(E){fr,to,w};
}
inline int q(int x){
    register int t=x,i=x,temp;
    while(r[t]!=t) t=r[t];temp=t;
    while(r[i]!=i) {temp=r[i];r[i]=t;i=temp;}
    return t;    
}

inline bool in(int x,int y){return not(q(x)^q(y));}
inline void j(int x,int y){r[q(x)]=q(y);}

int f[maxn];
int n,m;
signed main(){
    n=qr(1LL);m=qr(1LL);
    RP(t,0,n) r[t]=t;
    register int t1,t2,t3;
    RP(t,0,n+1) f[t]=1LL<<50;
    RP(t,1,m){
    t1=qr(1);
    t2=qr(1);
    t3=qr(1);
    add(t1,t2,t3);
    f[t1]=Min(f[t1],t3+1LL);
    f[t2]=Min(f[t2],t3+2LL);
    }
    RP(t0,1,2) RP(t,0,n) f[t%n]=Min(f[t%n],f[(t-1+n)%n]+2LL);
    RP(t,0,n) add(t%n,(t+1)%n,f[t%n]);
    sort(e+1,e+cnt+1);ll ret=0;
    RP(t,1,cnt){
    if(not in(e[t].fr,e[t].to)){
        ret+=(ll)e[t].w;
        j(e[t].fr,e[t].to);
    }
    }
    cout<<ret<<endl;
    return 0;
}