【图机器学习】cs224w Lecture 3

目录

• Network Motifs
  • Configuration Model
• Graphlets
• How to Find Motifs and Graphlets
• Structural Roles

转自本人：https://blog.csdn.net/New2World/article/details/105291956

大量真实网络都有一个规律，即这些网络都是由一些 building block 构成，类似 Kronecker 图有大量的重复结构。而我们需要一种度量方式来衡量某个结构在图中的显著性。因此需要引入 motif 和 graphlet 这两个概念。

这一部分我还有一些概念没完全理解，所以在最后记录了一些问题等待以后回来解决。也欢迎有理解了的朋友帮忙解惑。

Network Motifs

这里实在无法确定 motif 的准确翻译是什么，干脆不翻译了。但它是什么东西还是得搞清楚的：在图中大量重复的模式被称为 motif。这个定义包含了三个要点

• 大量，就是多，比随机图多
• 重复，还是多
• 模式，即规模小的导出图^[1]

我们为什么需要这个 motif ？首先，既然这个概念的定义表明它在网络中大量存在，说明这个 motif 揭示了这个网络的一些普遍规律，比如食物链中的互利共生关系或竞争关系。同时我们可以依据这个规律预测一些我们可能还没有发现的网络中隐含的关系。

知道了 motif 的好处之后就需要找到一种方法来衡量它在网络中的显著性，也就是是否大量出现。最直接的方式就是挨个数，即 (N_i^{real})。那么这样就又遇到了需要参照的情况了，换句话说就是“我怎么知道 (N_i^{real}) 算不算多？”。

Configuration Model

既然需要参照，那就自己动手生成一个。但这个生成模型就不能像 ER 随机图模型一样简单的按概率取边了。因为我们想要了解一个 motif 在网络中是否大量重复出现，那么需要和真实网络有相似的度分布和聚类系数。因此我们需要生成一个各节点和真实网络有相同度的随机图。这样的模型被视为这个网络的零模型(null model)。

怎么做呢？首先我们将每个度为 (k_i) 的点拓展为 (k_i) 个迷你点一组的结构，然后随机连接这些迷你点。最后合并同一组的迷你点就能得到满足节点度条件的图。

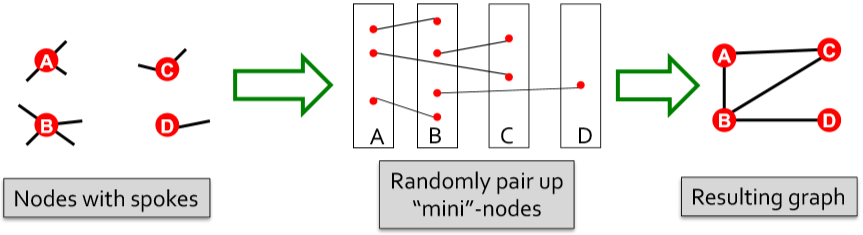
这里的确会出现自环和重边的问题，但需要清楚的是随着图的规模增大，节点数增加，相比于节点个数，每个节点的度(迷你点个数)是可以忽略不计的。也就是说这种自环和重边的情况很少发生。即使发生了，忽略就好，虽然会使得某些点的度不满足条件但不影响(反正都是随机图，差这个别几个点无所谓)。

还有一种方法，就是从给定的图开始，随机选择两条边然后将它们的端点交换。例如，(A ightarrow B,C ightarrow D)，交换后为 (A ightarrow D,C ightarrow B)。而交换次数大致是 (Q imes|E|)，其中 (Q) 需要取一些比较大的数，比如 (100)。直观理解就是让每条边平均交换 (Q) 次。
注意：这里交换就需要避免自环和重边了。因为随机的次数很多，如果不考虑自环和重边，最后可能导致这两种边大量出现且图会不连通。

当然，很明显，第一种方法更有效率……

---

这样有了参照之后我们就能数出来随机图里 motif 的出现次数 (N_i^{rand})。那我们将 motif 的显著性定义为：

[egin{aligned} Z_i&=(N_i^{real}-ar{N}_i^{rand})/std(N_i^{rand}) \ SP_i&=Z_i/sqrt{sumlimits_jZ_j^2} end{aligned}]

这里 (Z_i) 是节点 (i) 的显著性；(SP_i) 是归一化后所有候选的 motif 的显著性向量，它揭示了所有 motif 间的相对显著性关系，有了对比一切都明了了。至于需要生成多少随机图才能得到一个较为准确的标准差，Jure 的回答是：(100,1000,10000)，反正大于 (10)

虽然这里介绍的 motif 很简单，就是一些 pattern。但我们可以将这个概念拓展。例如，可以加入节点类型，就算网络结构一致但节点类型不一样也算不同的 motif；或者还可以加上时序信息。另外，还可以定义不同的显著性度量方法、对零模型加上不同的限制条件等。^[2]

Graphlets

motif 是从整个图中提取结构信息，那么如果我们要考虑一个局部或者一个节点周围的结构信息呢？我们引入了 graphlets 概念。graphlets 是一系列连通的非同构子图，这里要求是导出子图，即 induced。如下图，没有标字母的就是对称的或位于非同构位的节点。

这里提到了一个自同构轨道(automorphism orbit)^[3]的概念，不太清楚，记录下

类似于节点的度，定义 graphlet degree 为包含节点的 graphlet 的个数。对于有不同非同构位的 graphlet 要针对不同位置各自计算，以此得到 Graphlet Degree Vector (GDV)。

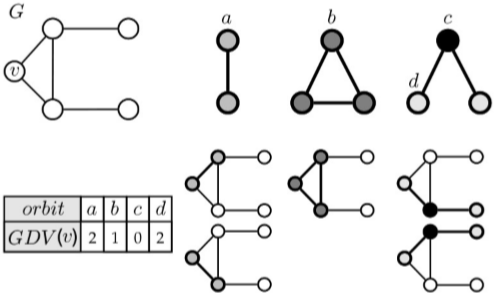
统计了节点数从 (2) 到 (5) 的 graphlets 后我们能得到一个长度为 (73) 的 GDV 向量来表示一个节点周围的结构信息，而这个信息覆盖了以该节点为中心 (4) 个 hops 内的区域。

How to Find Motifs and Graphlets

一般来说，合适的 motif 的规模就 (3)~(8) 个点，如果大了的话这个计算量就爆炸了。而且判断两个图是否同构的问题本身就是个 NP-complete 问题。那么计数一个图里的子图个数主要分两步：1. 枚举；2. 计数。现在又几种有效的算法来对子图进行枚举：

• Exact Subgraph Enumeration (ESU) [Wernicke 2006]
• Kavosh [Kashani et al. 2009]
• Subgraph Sampling [Kashtan et al. 2004]

Jure 主要介绍了 ESU，这个算法和找一个集合的所有子集的方法差不多，都是递归进行遍历。它定义了两个集合 (V_{subgraph}) 和 (V_{extension})，分别代表 当前已经生成了的子图节点 和 后续遍历的候选节点。其主要思路是：从一个起始点开始，每次往 (V_{extension}) 里加满足一下条件的点：

• 节点序号必须要大于起始点
• 新节点可以互相邻接，但不能跟任何已经在 (V_{subgraph}) 里的点邻接

ESU 算法运行后会生成一棵 ESU 树，如下图^[4]

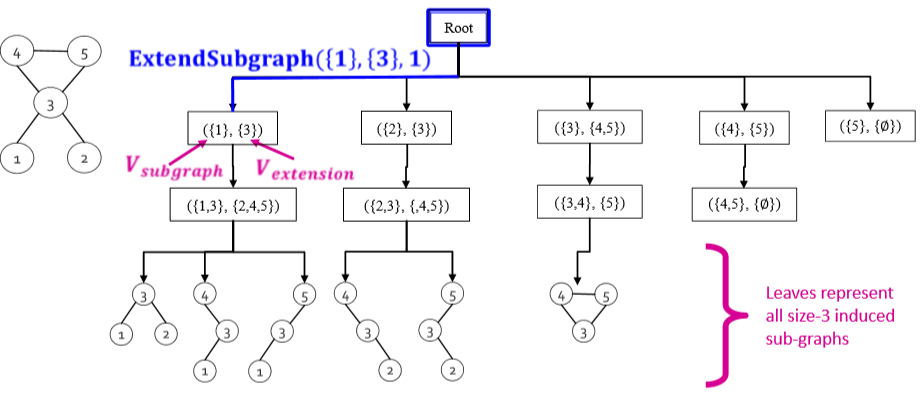
根据 ESU 的输出我们就可以来数同构的结构个数了，比如上图中画出的子图总共有两种非同构结构，第一种出现了 (5) 次，第二种只出现了 (1) 次。而图的同构算法这里采用的是 McKay's nauty [McKay 1981] 算法。这是一种启发式的算法，具体细节这里不做深入介绍，有时间了会写一篇 cs224w 里出现的算法汇总。

这里附带了同构图的定义：
如果存在这么一种双射关系 (f)，使得在图 (G) 中邻接的任意两个节点 (mu, u) 在图 (H) 中有对应的 (f(mu)) 和 (f( u)) 邻接，那么就说图 (G) 和 (H) 同构。

---

Structural Roles

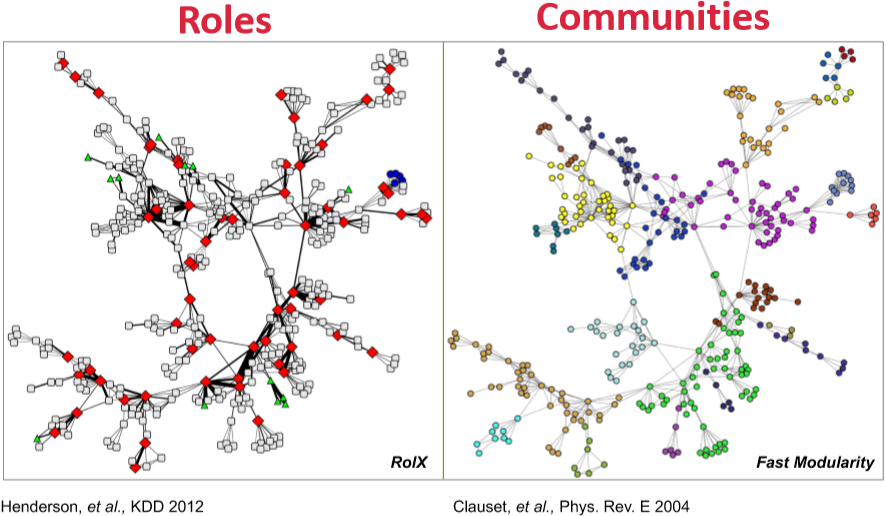
在现实中的真实网络里，不同节点可能扮演不同角色，比如食物链中的捕食者和被捕食者，企鹅群里的群主、管理员和群成员等等。而不同角色的节点周围的网络结构多多少少会有些差异，比如星型结构的中心、聚集的小团体或一些外围节点。研究这些不同角色的节点也可以告诉我们一些网络中隐含的信息。
角色的定义是在网络中具有相似位置的点的集合。这个定义和 community 其实是互补的，比如各个公司可能是不同的 community，而每个公司内部的角色大致是相同的(管理层和下属员工)。公司(community)内个体间会有比较密切的联系，但公司间相同职位(角色)的个体并不一定会有关联。

这里定义了 structural equivalence：若两节点与其他所有节点具有完全相同的连接关系，那么这两个节点就具有相同结构。然而这个定义太死板了，我们只想找到相似的结构，因此在这个定义的基础上我们允许一些 noise

---

既然有了定义，那么我们就要从网络中找出不同角色。有了角色信息后我们就可以：

• 发现一些异常行为
• 迁移学习，预测其它网络角色
• 计算网络相似度和迁移兼容性

这里介绍的算法是 RolX，这是一种

• 无监督学习
• 不需要先验知识
• 复杂度和边的数量成线性关系
• 能发现不同角色间的多种关系

这个算法的流程很直接，提取信息，然后聚类即可。大致流程可以归纳为：

graph LR Input(Adjacency Matrix)-->FeatExt[Recursive Feature Extraction] FeatExt-->NodeFeat(Node Feature Matrix) NodeFeat-->RoleExt[Role Extraction] RoleExt-->NodeRole(Node Role Matrix) RoleExt-->RoleFeat(Role Feature Matrix)

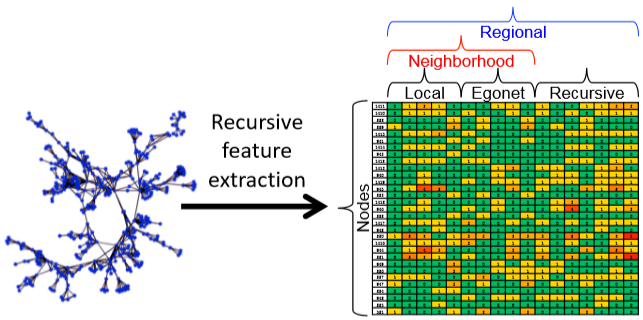
重点在特征提取这一步，特征包括了局部，ego和递归信息：

• 局部信息，比如之前提到的 GDV、节点的度等
• egonet 内的边的数量、egonet 与其他节点连接的边的数量等都能作为特征
• 递归信息这个概念很抽象，比如邻接节点的平均度、前面局部和 ego 信息的均值及总和等等。(甚至可以求和的结果和前面所有信息一起在求和或者均值，递归嘛)

不过特征太多也不见得是好事，因此会去除一些相关度高的特征以达到剪枝的目的。

egonet：包括一个节点、该节点的邻接节点以及这些节点间所有边的子图

最后一步使用聚类方法进行节点的角色聚类，可以使用 K-Means 等。而 RolX 中使用的是 Non-Negative Matrix Factorization，同时使用 MDL(最小描述长度) 来选择模型，KL 散度来度量 likelihood

---

1. Jure 的 slide 定义 motif 是 induced，但 wikipedia(https://en.wikipedia.org/wiki/Network_motif; https://en.wikipedia.org/wiki/Graphlets) 定义的 motif 不一定是 induced ↩︎

2. overrepresentation 和 underrepresentation (anti-motif) 的概念不太清楚
   ↩︎

3. automorphism orbit 的具体定义是什么？graphlets 里的非同构位是不是就是 automorphism orbit？ ↩︎

4. Jure 在课程视频 58:08 的地方回答学生问题说到 ESU 树输出的两个同构的子图是不同的 motif。有点迷惑：motif 不应该是一个 pattern 吗？这俩输出的不应该是 subgraph 吗？这俩到底是同一个 motif 不同 subgraph 还是如 Jure 说的不同 motif？ ↩︎