HDU

原题链接

题意：

一颗苹果树上有 $n$ 个苹果， 编号从 $1...n$ ，问最多取 $m$ 个苹果有多少种取法。

思路:

就是求 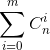      但是 $T, n ,m$ 均是 $1e5$ 的范围，直接求肯定爆炸，但此题只有查询，我们就可以用莫队来做，离线查询从而减少复杂度；

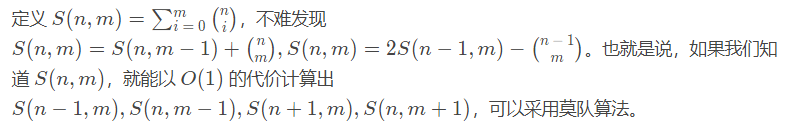
以上性质可推导求得，然后我们就可以用莫队进行状态的转移；

/*
* @Author: windystreet
* @Date:   2018-08-03 14:45:03
* @Last Modified by:   windystreet
* @Last Modified time: 2018-08-03 16:42:19
*/
#include<bits/stdc++.h>

using namespace std;

#define X first
#define Y second
#define eps  1e-2
#define gcd __gcd
#define pb push_back
#define PI acos(-1.0)
#define lowbit(x) (x)&(-x)
#define bug printf("!!!!!
");
#define mem(x,y) memset(x,y,sizeof(x))

typedef long long LL;
typedef long double LD;
typedef pair<int,int> pii;
typedef unsigned long long uLL;

const int maxn = 1e5+2;
const int INF  = 1<<30;
const int mod  = 1e9+7;

struct node
{
    LL n,m,id;
}s[maxn];
LL ans[maxn],inv[maxn],fact[maxn];
LL sq,tot;
bool cmp(node a, node b){
    if(a.n/sq == b.n/sq) return a.m < b.m;
    return a.n/sq <b.n/sq;
}
LL qpow(LL x,LL y){
    LL res = 1;
    while(y){
        if(y&1)res = (LL)res*x*1ll%mod;
        x = x * x % mod;
        y >>= 1;
    }
    return res; 
}
void init(){
    fact[0] = 1;
    for(int i = 1;i < maxn;i++){
        fact[i] = fact[i-1]*i%mod;             // 预处理阶乘 
    }
    inv[maxn-1] = qpow(fact[maxn-1],mod-2);    // 预处理逆元
    for(int i=maxn-2;i>=0;i--){
        inv[i] = inv[i+1]*(i+1)%mod;
    }
}

LL C(LL n,LL m){                               // 组合数
    return (fact[n] * inv[m] %mod) * inv[n-m] % mod;
}

void solve(){
    int t; tot = 0;
    init();
    scanf("%d",&t);
    for(int i=1;i<=t;i++){
        scanf("%lld%lld",&s[i].n,&s[i].m);
        s[i].id = i; tot = max(tot,s[i].n); 
    }
    sq = sqrt(tot);
    sort(s+1,s+1+t,cmp);
    LL L=1,R=-1,res = 0;
    for(int i=1;i<=t;i++){                      // 莫队部分，每次进行状态转移
        while(L<s[i].n){res = ((2*res - C(L++,R))+mod)%mod;}
        while(L>s[i].n){res = ((res + C(--L,R))%mod*inv[2]%mod)%mod;}
        while(R<s[i].m){res = (res + C(L,++R))%mod;}
        while(R>s[i].m){res = (res - C(L,R--)+mod)%mod;}
        ans[s[i].id ] = res;
    }
    for(int i=1;i<=t;i++){
        printf("%lld
",ans[i]);
    }
    return;
}

int main()
{
//    freopen("in.txt","r",stdin);
//    freopen("out.txt","w",stdout);
//    ios::sync_with_stdio(false);
    int t = 1;
    //scanf("%d",&t);
    while(t--){
    //    printf("Case %d: ",cas++);
        solve();
    }
    return 0;
}

比赛时没有做出来，真的蒟蒻